一、线性回归之Excel
1.线性回归—身高体重分析
1)在Excel中打开需要进行线性拟合的身高与体重数据
2)选择数据个数为20,对数据进行绘图,如下:
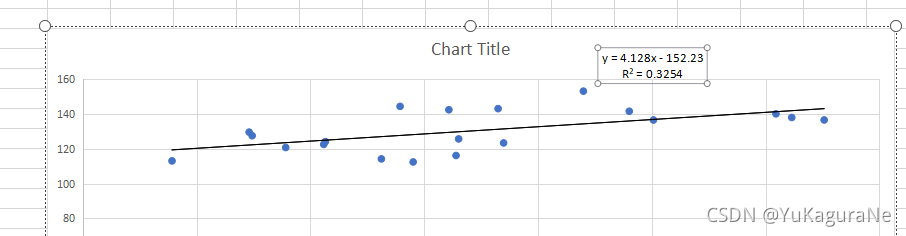
可得到回归方程为y=4.128x-152.23
相关系数为R2=0.3254
3)将选择的数据个数调整为200,绘图如下:
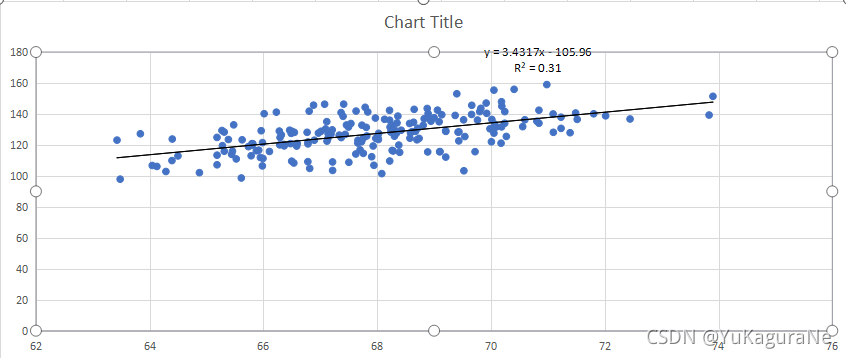
当数据个数增多,回归方程发生改变。
回归方程为y=3.4317x-105.96
相关系数为R2=0.31
4)继续将选择的数据个数增大,调整为20000,绘图如下:
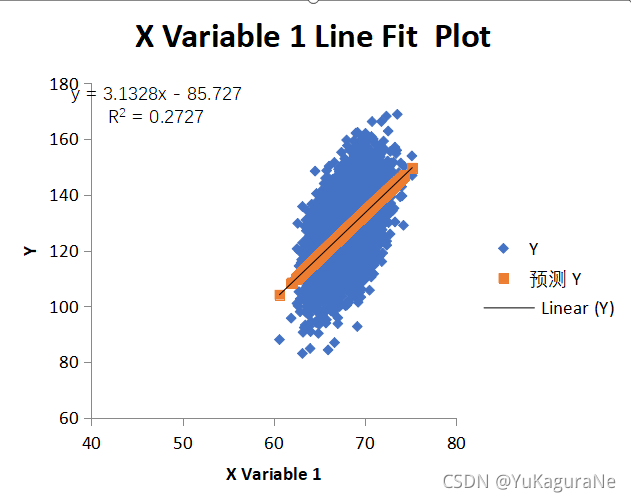
回归方程为y=3.1328x-85.727
相关系数为R2=0.2727
二、jupyter调用sklearn库解线性回归
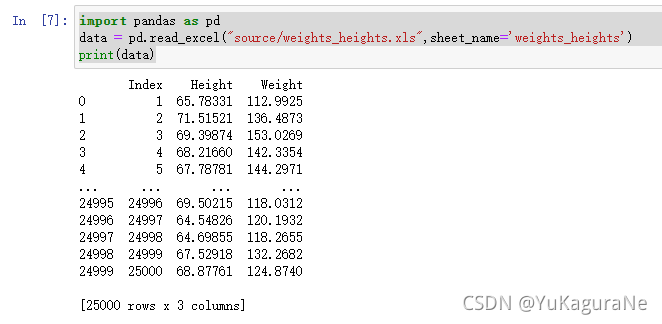
1.引入数据
代码如下:
import pandas as pd
data = pd.read_excel("source/weights_heights.xls",sheet_name='weights_heights')
print(data)
2.将数据画散点图
代码如下:
import matplotlib.pyplot as plt
data.plot.scatter(x='Height',y='Weight')
plt.show()
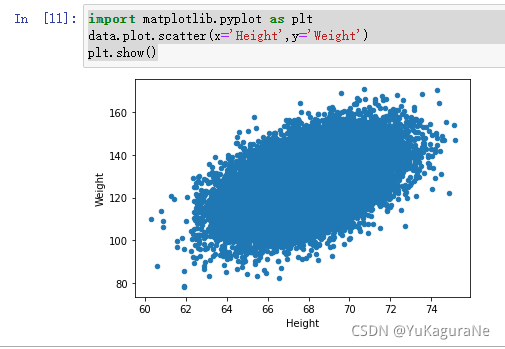
3.调用sklearn库
调用sklearn库
#调用sklearn库做线性回归
from sklearn.linear_model import LinearRegression
features = data['Height'].values.reshape(-1,1)
target = data['Weight']
regression = LinearRegression()
model = regression.fit(features,target)
输入代码
model.intercept_
运行结果如下
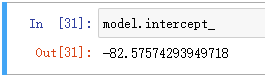
继续运行下列代码
model.coef_
运行结果:
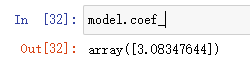
接下来使用predict()函数即可预测目标target的值