Chapter6:求解微分问题
6.求解微分问题
6.1 使用定义求导
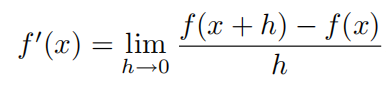
遇到
0
0
\frac{0}{0}
00?的不定式,基本思想是通过通分来化简分子
例子:

6.2 用更好的办法求导
一个函数求导的关键是,理解它是如何由简单函数合成的
6.2.1 函数的常数倍
g ( x ) = c f ( x ) g ′ ( x ) = c f ′ ( x ) g(x)=cf(x)\\ g'(x)=cf'(x) g(x)=cf(x)g′(x)=cf′(x)
6.2.2 函数和与函数差
g ( x ) = f ( x ) + h ( x ) g ′ ( x ) = f ′ ( x ) + h ′ ( x ) g ( x ) = f ( x ) ? h ( x ) g ′ ( x ) = f ′ ( x ) ? h ′ ( x ) g(x)=f(x)+h(x)\\ g'(x)=f'(x)+h'(x)\\ g(x)=f(x)-h(x)\\ g'(x)=f'(x)-h'(x) g(x)=f(x)+h(x)g′(x)=f′(x)+h′(x)g(x)=f(x)?h(x)g′(x)=f′(x)?h′(x)
6.2.3 通过乘积法则求积函数的导数
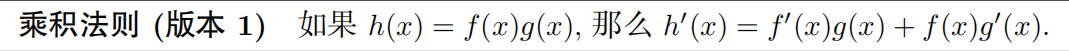


每一个变量都做一次微分运算
6.2.4 通过商法则求商函数的导数


6.2.5 通过链式求导法则求复合函数的导数
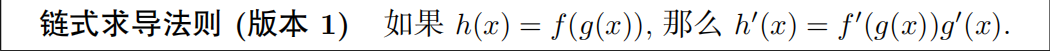

d
y
d
x
\frac{dy}{dx}
dxdy?并不是分数,它们是分数
Δ
y
Δ
x
\frac{\Delta y}{\Delta x}
ΔxΔy?的极限,不能进行约分

例子:

6.2.6 复杂函数求导例子
复杂函数分解为简单函数,然后使用链式法则进行求导

6.2.7 乘积法则和链式求导法则的证明
证明两个函数的乘积法则
两个量
u
,
v
u,v
u,v 都依赖于某个量
x
x
x,如果
x
x
x 有一个小的变化量
Δ
x
\Delta x
Δx,乘积
u
v
uv
uv 将如何变化 ?
u
u
u 变成
u
+
Δ
u
u+\Delta u
u+Δu
v
v
v 变成
v
+
Δ
v
v+\Delta v
v+Δv
u
v
uv
uv 变成
(
u
+
Δ
u
)
(
v
+
Δ
v
)
(u+\Delta u)(v+\Delta v)
(u+Δu)(v+Δv)


面积改变 Δ ( u v ) = u Δ v + v Δ u + Δ u Δ v \Delta(uv)=u\Delta v+v\Delta u+\Delta u\Delta v Δ(uv)=uΔv+vΔu+ΔuΔv
当量 Δ u \Delta u Δu 和 Δ v \Delta v Δv 非常小时, Δ u Δ v \Delta u\Delta v ΔuΔv事实上会非常非常小,基本忽略不计
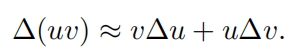
将上式除以
Δ
x
\Delta x
Δx ,然后取极限,近似符号就会变为等号,得到乘积法则
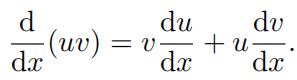
证明三个函数的乘积法则


链式求导法则证明
u = g ( x ) u=g(x) u=g(x) 当 x x x 变化 Δ x \Delta x Δx时, u u u变化可近似看成 g ′ ( x ) g'(x) g′(x) 乘以 x x x 的变化(可将 g ′ ( x ) g'(x) g′(x) 看作是一种拉伸因子)【Chapter5 中 5.2.7 作为极限比的导数阐释了这种思想】
当
x
x
x 变化
Δ
x
\Delta x
Δx时,
u
u
u 变化
g
′
(
x
)
Δ
x
g'(x)\Delta x
g′(x)Δx
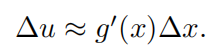
y
=
f
(
u
)
y=f(u)
y=f(u),
u
u
u 变化
Δ
u
\Delta u
Δu,
y
y
y 变化
f
′
(
u
)
Δ
u
f'(u)\Delta u
f′(u)Δu
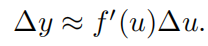
替换
Δ
u
\Delta u
Δu
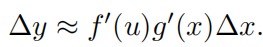
x
x
x 的变化首先被因子
g
′
(
x
)
g'(x)
g′(x) 拉伸了,然后又被因子
f
′
(
u
)
f'(u)
f′(u) 拉伸了
上式左右同除以
Δ
x
\Delta x
Δx 然后取极限
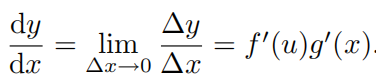
链式求导法则的第一种形式
u
=
g
(
x
)
,
y
=
f
(
u
)
u=g(x),y=f(u)
u=g(x),y=f(u),得到
y
=
h
(
x
)
=
f
(
g
(
x
)
)
y=h(x)=f(g(x))
y=h(x)=f(g(x))

链式求导法则的第二种形式
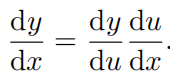
6.3 求切线方程

6.4 速度和加速度
时刻
t
t
t 的位置
x
x
x
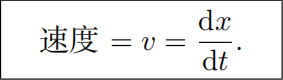

6.5 导数伪装的极限
给出的极限在形式上与导数定义类似
如果使用洛必达法则,甚至不需要去识别一个极限是否是一个伪装的导数
例子:

例子:

6.6 分段函数的导数

例子1:
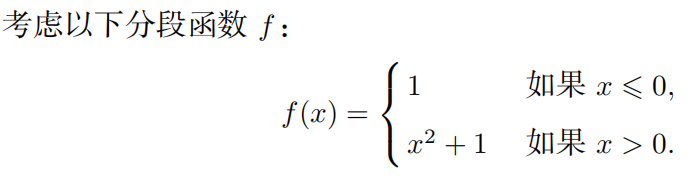

检验连接点上的连续性
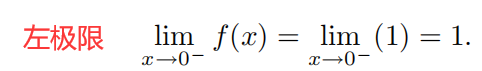

左极限
=
=
= 右极限,则双侧极限存在且等于
1
1
1,双侧极限与
f
(
0
)
f(0)
f(0)处的值相等,故函数在连接点
x
=
0
x=0
x=0 上连续
检验连接点上的可导性
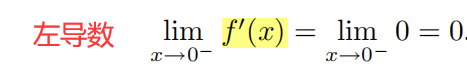
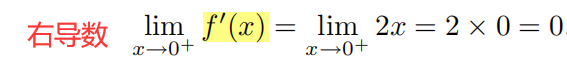
左导数
=
=
= 右导数,所以函数在连接点
x
=
0
x=0
x=0 处可导
例子2:

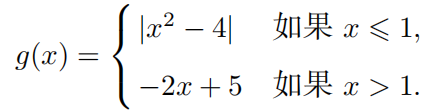


检验函数在连接点
x
=
?
2
x=-2
x=?2 上的情况
检验连接点上的连续性
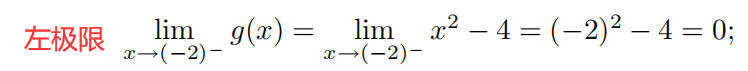
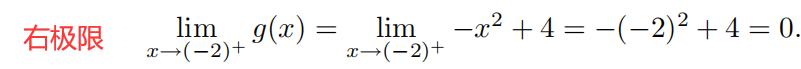
左极限
=
=
= 右极限,则双侧极限存在且等于
0
0
0,双侧极限与
f
(
?
2
)
f(-2)
f(?2)处的值相等,故函数在连接点
x
=
?
2
x=-2
x=?2 上连续
检验连接点上的可导性
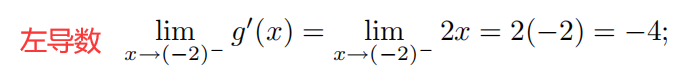
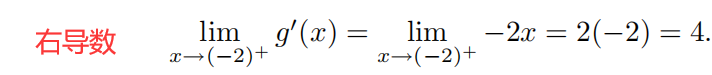
左导数 ≠ \neq ?= 右导数,函数在连接点 x = ? 2 x=-2 x=?2 处不可导
检验函数在连接点
x
=
1
x=1
x=1 上的情况
检验连接点上的连续性
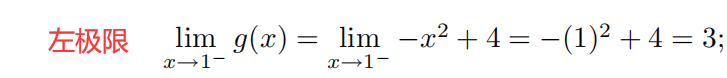
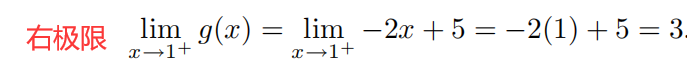
左极限
=
=
= 右极限,则双侧极限存在且等于
3
3
3,双侧极限与
f
(
1
)
f(1)
f(1)处的值相等,故函数在连接点
x
=
1
x=1
x=1 上连续
检验连接点上的可导性
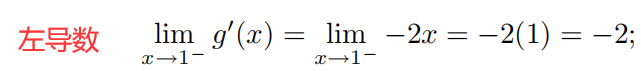
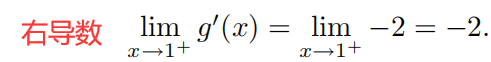
左导数 = = = 右导数,函数在连接点 x = 1 x=1 x=1 处可导
6.7 直接画出导函数的图像




