[人工智能]使用Python代码实现一个简单的分子动力学模拟程序

1. 前言

理解分子动力学模拟最好的方法是编写一个分子动力学程序，换句话说，教会计算机去理解并做执行，自己才算理解会了。因此本文将从常用于描述分子间的非键相互作用中的Lennard-Jones potential讲起，最后将其应用到一个简单的分子动力程序中，来模拟二维空间下流体的分子动力学行为，为了更加直观的理解和展示这一过程，本文主要是Python代码实现相关的代码和程序，并使用jupyter notebook来进行编码展示和描述，会尽可能的解释出每一行代码的含义，让分子动力学模拟的初学者和爱好者能从0到1编写出一个初级的分子动力学小程序，以加深对分子动力学模拟过程的理解。

2. 分子间相互作用力

2.1 简介

根据现代物理力学理论可知，力的本质其实就是宇宙中存在的四种相互作用，按照从强到弱的顺序，排在第一的是强相互作用，其可以使原子核里面的质子，中子稳定地存在。排在第二的是电磁相互作用，它贡献了化学键，分子间相互作用力，以及各种宏观世界的的力，比如表面张力，静电力，磁力等等。 排在第三的是弱相互作用，其也只有在原子核内有效，而且强度非常弱，虽然没有什么存在感，但是很重要，排在最后就是万有引力了，其强度极弱，对物质的性质没有可观察的影响，可以忽略不计了。

在这里主要介绍由电磁相互作用引起的分子间相互作用力，亦称分子间引力，是介导分子间相互作用的力，包括作用于原子和其他类型的相邻粒子（例如原子或离子）之间的吸引力或排斥力。分子间相互作用力(非键相互作用) 相对于分子内相互作用力（键相互作用） 来说是微弱的。例如，涉及原子之间共享电子对的共价键比相邻分子之间存在的力强得多。这两组力都是分子力学中常用力场的重要组成部分。

分子间相互作用力，它主要包括：

范德华力（Van der Waals force）：起初为了修正范德华方程而提出。普遍存在于固、液、气态任何微粒之间，与距离六次方成反比。
次级键（secondary bond）： 键长长于共价键、离子键、金属键，但短于范德华相互作用的微观粒子相互作用。

1. 氢键（Hydrogen bonding）：氢与氮、氧、氟所键结产生的作用力。
2. 非金属原子间次级键：存在于碘单质晶体中。
3. 金属原子与非金属原子间次级键：存在于金属配合物中。
4. 亲金作用。
5. 亲银作用。
   此外科学家也不断研究新的分子间作用力，包括双氢键和金键等。

2.2 范德华力

范德华力（英语：van der Waals’ Forces；又名:范德瓦耳斯力）在化学中指分子或非极性原子（稀有气体）之间非定向的、无饱和性的、较弱的相互作用力，包括排斥力和吸引力。根据荷兰物理学家van der Waals（约翰内斯·范德瓦耳斯）命名，其于1910获得Noble物理奖。范德华力是分别来自两个分子中的一种中性原子之间通过瞬间静电相互作用产生的一种弱的分子之间的力，这是由于附近粒子波动极化的相关性引起的（量子动力学的结构），具体而言，电子密度可能会暂时更大地转移到原子核的一侧。这会产生一个瞬态电荷，附近的原子可以被吸引或排斥。但它比化学键或共价键弱得多，通常其能量小于5kJ/mol（0.4~4kJ/mol）。当两个原子之间的距离为它们的范德华半径之和时，范德华引力最强。强的范德华排斥作用可以防止原子相互靠近。范德华力的大小和分子的大小成正比。

在介绍范德华力的来源前，先简单了解几个概念：

固有偶极：极性分子中由于组成元素不同，其吸引电子的能力各有差异（元素周期律），这就使得分子中有电子偏移的现象，这样就产生了极性，并且偶极持续存在，称为固有偶极。

诱导偶极：是指非极性分子在电场中或者有其他极性分子在较近距离的情况下，由于电子带负电，核带正电，它们会发生偏移，这种现象称为诱导偶极。

瞬时偶极：一切分子中，不管是极性分子还是非极性分子，原子核时刻在震动，电子时刻在运动、跃迁，在它们运动的时候，偶尔离开平衡位置而产生极性，只不过这个过程持续时间很短，故称瞬时偶极。

根据范德华力的来源可分为以下几个部分：

1.取向力（1912-Keesom force）：固有偶极之间的电性引力；(热平均固有偶极——固有偶极相互作用)

范德华力中吸引力的第一个贡献项是由于固有偶极子、四极子（所有对称性低于立方的分子）和多极子之间的静电相互作用。它被称为Keesom相互作用，以Willem Hendrik Keesom 的名字命名。这些力源于固有偶极子（偶极分子）之间的吸引力，并且与温度有关。
Fig 1.取向力示意图

它们由集合的偶极子之间的吸引力相互作用组成对偶极子的不同旋转方向进行平均。假设分子不断旋转并且永远不会被锁定到位。这是一个很好的假设，但在某些时候分子确实会被锁定到位。Keesom 相互作用的能量取决于距离的倒数六次方，而两个空间固定偶极子的相互作用能量取决于距离的倒数三次方。Keesom 相互作用只能发生在具有固有偶极矩的分子之间，即两个极性分子之间。Keesom 相互作用也是非常弱的范德华相互作用，不会发生在含有电解质的水溶液中。具有固有偶极矩${\mu }_i$和${\mu }_j$的分子i和j，其相互作用势能为：

$$E_e=?\frac{2}{3}\left[\frac{{\mu }_i^2{\mu }_j^2}{(4\pi {\epsilon }_0{)}^2{K}_{B}T}\frac{1}{r^6}\right]\text{\hspace{1em}(1)}$$
$E_e$表示随机取向的偶极相互作用的平均作用能

${\epsilon }_0$ :自由空间的介电常数

$T$: 温度

$K_B$:玻尔兹曼常数，

$r$:分子间距离。

2.诱导力（1921 Debye force）：诱导偶极与固有偶极之间的电性引力，如离子诱导偶极力和偶极诱导偶极力。(热平均固有偶极——诱导偶极相互作用)

第二个贡献为项称为感应力（极化）力或德拜力，这些力以荷裔美国物理化学家彼得德拜的名字命名。为具有极化率$\alpha$???的分子在周围分子固有偶极矩电场的作用下产生诱导偶极矩，诱导偶极矩与周围分子固有偶极矩的相互作用。当一个具有固有偶极子的分子排斥另一个分子的电子时，就会发生这些诱导偶极子。具有永久偶极子的分子可以在相似的相邻分子中诱导偶极子并引起相互吸引。原子之间不会发生德拜力。因为一般单原子并非分子，无极化率，而特殊当原子分子如惰性气体等，为非极性分子无固有偶极，它们之间没法互相诱导，故德拜力不会产生与原子之间。诱导偶极子和固有偶极子之间的力不像 Keesom 相互作用那样依赖于温度，因为诱导偶极子可以围绕极性分子自由移动和旋转。其相互作用的势能表示为：

$$E_p=?\frac{{\alpha }_i{\mu }_j^2+{\alpha }_j{\mu }_i^2}{4\pi {\epsilon }_0}\frac{1}{r^6}\text{\hspace{1em}(2)}$$

当具有永久偶极子的分子（例如 HCN）与没有分子偶极子的分子碰撞时，碰撞本身会通过分子内电子密度的变化导致偶极子出现。HCN 中的氮原子富含电子，分子偶极子指向该原子的方向。碰撞时，第二个原子的电子云会被氮上多余的电子密度排斥，因此带正电的原子核会更靠近 N 并与其相互作用。

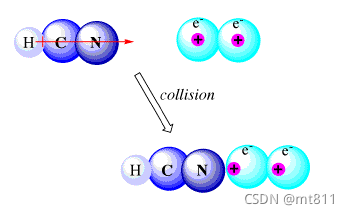
Fig 2.诱导力力示意图

3.色散力（London force）：瞬时偶极之间的电性引力；(诱导偶极——诱导偶极相互作用)

第三个也是主要的贡献是色散或伦敦力（波动偶极诱导偶极），由于分子中电子和原子核不停地运动,非极性分子的电子云的分布呈现有涨有落的状态,从而使它与原子核之间出现瞬时相对位移,产生了瞬时偶极,分子也因而发生变形。分子中电子数愈多、原子数愈多、原子半径愈大,分子愈易变形.瞬时偶极可使其相邻的另一非极性分子产生瞬时诱导偶极,且两个瞬时偶极总采取异极相邻状态,这种随时产生的分子瞬时偶极间的作用力为色散力(因其作用能表达式与光的色散公式相似而得名)。瞬间偶极距随时间不断变化，统计平均为0，因此实验测量得到的分子偶极距离任然为0，色散力作为一种相互吸引力，可以使得体系能量降低，一般地，极化的体积分别为${\alpha }_i$和${\alpha }_j$的两个分子或离子间色散能可以写成：

$$E_d=?\frac{3}{2}\left[\frac{I_i{I}_j}{I_i+I_j}\right]\left[\frac{{\alpha }_i{\alpha }_j}{(4\pi {\epsilon }_0{)}^2}\frac{1}{r^6}\right]\text{\hspace{1em}(3)}$$

虽然瞬时偶极存在暂短,但异极相邻状态却此起彼伏,不断重复,因此分子间始终存在着色散力.无疑,色散力不仅存在于非极性分子间,也存在于极性分子间以及极性与非极性分子间。色散力存在于一切分子之间.色散力与分子的变形性有关,变形性越强越易被极化,色散力也越强。稀有气体分子间并不生成化学键,但当它们相互接近时,可以液化并放出能量,就是色散力存在的证明.

所有分子通过伦敦色散力或诱导偶极相互作用。在下图中，一个2个原子的分子与一个3个原子的分子碰撞。第一个分子的电子云排斥它撞击的分子的电子云，导致一些电子密度远离原子核。原子核然后被它自己的电子屏蔽得很差，并吸引了第一个分子的电子云。

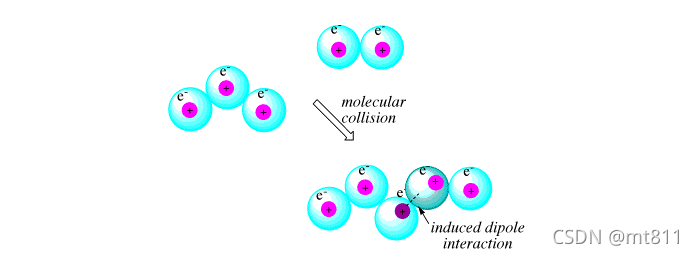
Fig 3.色散力示意图

4.由泡利不相容原理产生的排斥成分，可防止分子坍塌。
上面讨论的分子间相互作用均为吸引作用,并且势能随分子间距离的减小而降低。但是,这些关系并不适合分子相互靠得特别近的情况。当两个分子相互靠近,达到或接近电子云相互重叠的距离时,分子间的排斥作用将显著增加,引起体系势能的迅速升高。此外,原子核间的静电排斥作用,也引起体系的势能升高。完整的分子间相互作用函数必须同时考虑排斥作用的贡献。理论分析表明, 排斥作用对体系势函数的贡献与分子间的距离呈指数关系：
$$u(r)=Aexp(?\beta r)\text{\hspace{1em}(4)}$$

为了计算方便和效率，常把排斥能表示为幂函数的形式：

$$u(r)=A/r^n$$

式中，A为参数;n则在8~16中变化。同时排斥力也是一会走近程相互作用。随分子间距离增大而迅速衰减。当原子间距离低于0.4 nm 时，此时的对范德华力的贡献主要来自泡利不相容原理，让物质内部有所排斥，表现为排斥力。

Fig 4. 各分子范德华力吸引力的分配情况

可以说范德华力属于库伦相互作用（静电相互作用），但是我们经常看到分子间相互作用大体分为两种：静电相互作用和范德华力相互作用（广义的）。前面说到的范德华力属于静电相互作用，其为狭义的范德华力它通常指伦敦色散力（London dispersion force），它的相互作用能$E_d$与分子间距（r）是$\frac{1}{r^6}$的关系，而广义的范德华力，是因为Keesom force和Debye force在热平均后都与London force一样具有$\frac{1}{r^6}$的关系。如果没有热平均，偶极-偶极相互作用是$\frac{1}{r^3}$的关系也就是说Keesom force要更加短程，而相对短程也是范德华力（短程相互作用）区别于静电相互作用（长程相互作用）的特征。因此可以看出非键相互作用分类依据为两者相互作用随距离变化的衰减特点不同。

范德华力的主要特点是：

• 它们比普通的共价键和离子键弱。

• 范德华力是可加的，不能饱和。

• 它们没有方向特性。

• 它们都是短程力，因此只需要考虑最近粒子（而不是所有粒子）之间的相互作用。分子距离越近，范德华引力越大。

• 除了偶极-偶极相互作用之外，范德华力与温度无关。

• 在低分子量醇中，其极性羟基的氢键性质支配了其他较弱的范德华相互作用。在较高分子量的醇中，非极性烃链的性质占主导地位并决定了它们的溶解度。

2.2.1 Lennard-Jones potential 模型

Lennard-Jones potential,它以John Lennard-Jones.（约翰·伦纳德-琼斯）的名字命名被称为LJ势或者12-6势。它描述了简单原子和分子之间相互作用的基本特征：两个相互作用的粒子在非常近的距离相互排斥，在中等距离相互吸引，在无限距离上不相互作用，LJ势是一对势，即该势不包含三体或多体相互作用。LJ势是研究最广泛和最彻底的势，被认为是简单而现实的分子键相互作用的半经验模型。LJ势的常用表达式为：

$$E_{LJ}=4\epsilon \left[(\frac{\sigma }{r_{ij}}{)}^{12}?(\frac{\sigma }{r_{ij}}{)}^6\right]\text{\hspace{1em}(5)}$$

$E_{LJ}$:为两体之间的势能大小。

$\varepsilon $ :为控制相互作用的强度（以 eV 为单位）,从本质上讲，它衡量两体相互吸引的强度,通常称为势阱深度（也叫“色散能”）;

$\sigma$:为相互作用的势能正好为零时的两原子间的距离，$\sigma$给出了两个非键合粒子的接近程度的度量，因此被称为范德瓦尔斯半径。它等于非成键粒子之间核间距离的二分之一。

$r_{ij}$: 为i,j两体之间的距离。

在实际应用中，$\epsilon$,$\sigma$参数往往通过拟合已知实验数据或精确量子计算结果而确定。 另一种写法是：

$$E_{LJ}(r_{ij})=?\left[(\frac{r_{min}}{r_{i}j}{)}^{12}?2(\frac{r_{min}}{r_{ij}}{)}^6\right]（amber用的这个）\text{\hspace{1em}(6)}$$

$r_{min}=2^{\frac{1}{6}}\sigma =1.122\sigma$：为势阱底部时，两体间的距离。

物理背景

有很多方程能描述范德华相互作用，其中最常见的为LJ势函数。Lennard-Jones 势模拟了两个最重要和最基本的分子相互作用：其中排斥项($\frac{1}{r_{ij}^{12}}$)描述了在相互作用粒子的短距离上由于重叠电子轨道而产生的泡利斥力，吸引项($\frac{1}{r_{ij}^6}$)描述了长距离相互作用（主要为色散力）的吸引力，在两个粒子之间的无限距离处消失。短距离的陡峭排斥相互作用导致固相和液相的低压缩性；有吸引力的分散相互作用对凝聚相起到稳定作用，尤其是汽液平衡。

吸引项的函数形式，即指数“6”，具有物理上的合理性，对于具有指数“12”的排斥项并不严格。简单原子和分子之间有吸引力的色散相互作用是部分电荷波动的结果。量子化学计算表明，这种色散贡献必须以($\frac{1}{r_{ij}^6}$)的速度衰减。

($\frac{1}{r_{ij}^{12}}$) 项被使用，主要是因为它在计算上可以非常有效的实现为($\frac{1}{r_{ij}^6}$)的平方，这对于’12’以外的值不成立。此外，($\frac{1}{r_{ij}^{12}}$) 合理地接近了泡利斥力，可以使用任意指数而不是12和6来推广Lennard-Jones势能，在这里我们仅讨论LJ 6-12.

下面以单原子分子氩为例，应用LJ势能函数描述氩-氩间的相互作用，使用以下Python代码定义了LJ势的每个组成部分和相互作用的总能量。然后将氩-氩间LJ势能的变化绘制在一张图上。$?$和$\sigma$?的值是与氩-氩相互作用有关的值。

#内嵌绘图
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

#1.LJ势能函数主要代码：...............................................................

#定义吸引力项
def attractiveEnergy (r,epsilon,sigma):
   return  -4 * epsilon * np.power(sigma/r,6)

#定义排斥项
def repulsiveEenergy(r,epsilon,sigma):
   return 4 * epsilon * np.power(sigma/r,12)

#定义LJ 6-12 势能函数
def ljEenergy(r,epsilon,sigma):
   return attractiveEnergy(r,epsilon,sigma) + repulsiveEenergy(r,epsilon,sigma)

#.....................................................................................


#2.图像绘制....................................................
#画氩-氩原子间的LJ相互作用图像（参数：a=epsilon; b=sigma）
a=0.0103  
b=3.4
#预设氩-氩原子为3到8埃，产生以下100个系列数据
r=np.linspace(3.0,10,100)

#绘制吸引相互作用图像
plt.plot(r,attractiveEnergy(r,a,b),label="Attractive")

#绘制排斥相互作用图像
plt.plot(r,repulsiveEenergy(r,a,b),label="Repulsiver")

#绘制
plt.plot(r, ljEenergy(r, a, b), 
         label='Lennard-Jones')

#横纵坐标名称
plt.xlabel(r'$r$(?)')
plt.ylabel(r'$E$(eV)')
plt.legend(frameon=False)

#选区X,Yz轴一些显示范围，一更好展示两原子间的作用变化趋势
plt.xlim([2.9, 8])
plt.ylim([-0.018, 0.034])

#以下为图表中的注释信息............................................................
#在（0,0）处绘制水平虚线
plt.hlines(0, 0, 8, colors = "black", linestyles = "dashed")

# 绘制势阱深度espsilon,此时两原子键距离为：r=1.122*\sigma=3.8148
plt.annotate(s='$r_{min}=1.122 \sigma$', weight='heavy',xy=(3.8148, -0.0103), xytext=(5, -0.0103),
arrowprops=dict(arrowstyle='<-',))

plt.annotate(s='',xy=(3.8148, -0.0103), xytext=(3.8148, 0), 
             arrowprops=dict(arrowstyle='<->',color='red'))
plt.annotate(s='',xy=(2.91, 0), xytext=(3.4, 0), 
             arrowprops=dict(arrowstyle='<->',color='red'))

plt.text(3.9, -0.006, r'$\varepsilon$', fontsize=20)
plt.text(3, 0.003, r'$\sigma$', fontsize=20)

# 绘制图像
#plt.show() # 有了%matplotlib inline 就可以省掉plt.show()了

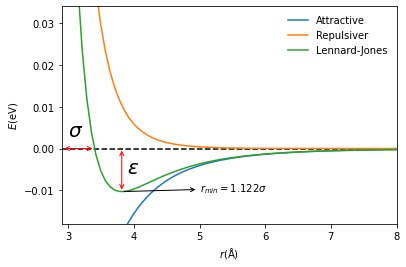
***Fig 5.以上Python代码生成了氩原子分子间LJ势能随两者之间变化的函数图像***

数学表示

除了以上的等式之外，还有几种不同的形式来表示LJ势能函数。

AB型：

AB形式经常被用于仿真软件的实现，因为它方便计算，其表示的就是LJ势

$$E_{LJ}=\frac{A}{r_{ij}^{1}2}?\frac{B}{r_{ij}^5}\text{\hspace{1em}(7)}$$

其中：

$A=4\epsilon {\sigma }^{12}$

$B=4\epsilon {\sigma }^6$

$\sigma =\sqrt[6]{\frac{A}{B}}$

$\epsilon =\frac{B^2}{4A}$

LJ势 n-m型：

在LJ势函数中，指数12和6分别与排斥力的硬度的和吸引力的作用范围有关。对多数有机分子来说，用$(\frac{1}{r_{ij}^6})$近似吸引势函数，效果良好，但是用$(\frac{1}{r_{ij}^{12}})$近似排斥部分，则排斥势太陡了，不如用$\frac{1}{r_{ij}^9}$和$\frac{1}{r_{ij}^{10}}$更适合实际分子。这个时候如果只是调整参数A和B（或者$\epsilon$和$\sigma$?）,就无法达到更好的效果，因此可以用通式表示势函数：

$$E_{LJ}=\frac{{\epsilon }_{ij}}{n?m}(\frac{n^n}{m^m}{)}^{\frac{1}{n?m}}\left[(\frac{\sigma }{r_{ij}}{)}^n?(\frac{\sigma }{r_{ij}}{)}^m\right]\text{\hspace{1em}(8)}$$

第一项为原子实的排斥力，n越大原子实越硬；第二项为吸引的作用范围，m越小吸引力的作用范围越大,在实际应用时，常用的LJ 12-10势函数近似氢键，LJ 12-3势函数近似金属原子键的相互作用，效果较好。

在分子模拟中的应用

LJ势不仅在在计算化学和软物质物理学中至关重要，而且对于真实物质的建模也是如此。使用LJ势计算出的宏观特性，一方面与氩气等简单物质的实验数据有很好的一致性，另一方面势函数$E_{ij}$与量子化学的结果有相当的一致性。同样的，LJ势对液相中的分子相互作用有很好的描述，而对固相中的分子相互作用则只有大致的描述。这主要是由于多体相互作用在固相中起着重要作用，而LJ势中不包括这些作用。因此，LJ势被广泛用于软物质物理学和相关领域，而在固体物理学中却不常使用。由于其简单性，经常被用来描述气体和简单流体的特性，并在分子模型中建立色散和排斥相互作用的模型。它对惰性气体原子和甲烷特别准确。此外，对于中性原子和分子的长距离和短距离的分子相互作用计算，它也能产生一个很好的近似值。因此，LJ势经常被用作复杂分子（如烷烃或水）的分子模型的构建模块（力场中的非键相互作用势能项）。大量的力场都是基于LJ势，例如TraPPE力场,OPLS力场,和MolMod力场,（对分子力场的概述不在本文讨论范围之内）对于最先进的固态材料建模，使用了更复杂的多体势（如EAM势）。此外LJ势还可用于模拟固-液界面上的吸附作用，即物理吸附或化学吸附。

3. 分子动力学模拟程序

3.1 简介

分子动力学方法的基本思想是根据分子的势能函数（力场），得到作用在每个原子上的力，利用牛顿第二定律求解运动方程，得到原子在势能面上的运动轨迹，从而达到构象搜索的目的。

从经典力学角度分析，分子体系是由一组具有分子内和分子间相互作用的原子组成的力学体系。由原子核集中了原子的主要质量，分子中个原子可以近似地看成位于相应原子核位置的一组质点，因此分子体系可以近似为质心力学体系：

分子内和分子间的相互作用通常由分子体系的势能函数所描述（力场），根据经典力学，系统中的作用在原子i上的力为势能的梯度，如下：

$$\begin{array}{rl}{F}_i& =?{▽}_{i}E\\ & =?\left(i\frac{?}{?x_i}+j\frac{?}{?y_i}+k\frac{?}{?z_i}\right)E\end{array}\text{\hspace{1em}(9)}$$

由牛顿定律，可得到i原子的加速度为：
$$a_i=\frac{F_i}{m_i}\text{\hspace{1em}(10)}$$

将牛顿定律方程式对时间积分，可以预测i原子经过时间t后的速度和位置

KaTeX parse error: No such environment: align* at position 8: \begin{?a?l?i?g?n?*?}? \begin{aligned…

式中 $r$和$v$分别为粒子的位置与速度，上标“0”表示为各物理量的初始值。?

分子动力学模拟可以用于研究LJ势能和获得“伦纳德-琼斯物质” 的热物理特性。LJ势通常是发展物质（特别是软物质）理论的标准选择，也是发展和测试计算方法以及算法的选择，根据实际物质的特性调整参数模型$\epsilon$和$\sigma$后,LJ势便可很准确地的描述简单物质（惰性气体）。

使用分子动力学模拟研究由LJ势能模型所组成的氩原子分子体系时，其分子体系为仅包含分子间相互作用组成的力学体系(即力场仅使用LJ势构建)，分子间相互作用LJ势能函数来描述，根据经典力学，分子体系之间的相互作用力可以用LJ势导出，如下：

$$\begin{array}{rl}F(r_{ij})& =?▽E_{LJ}\\ & =?\frac{d{E}_{LJ}}{dr}\hat{r}\\ & =4?\left[12\frac{{\sigma }^{12}}{r_{ij}^{13}}?6\frac{{\sigma }^6}{r_{ij}^7}\right]\hat{r}\\ & =48?\left[\frac{{\sigma }^{12}}{r_{ij}^{13}}?24?\frac{{\sigma }^6}{r_{ij}^7}\right]\end{array}\text{\hspace{1em}(12)}$$

到目前为止，我们已经基本了解了分子动力学模拟和LJ势的基本原理，接下来让我开始为二维空间的氩原子分子体系模拟创建一个分子模拟小程序，在这里所创建的程序遵循最少必要知识原则，会尽可能的简单以便阐明分子动力学模拟的一些重要的特征。

程序按以下方式构成：

（1）读入指定运算条件的参数（初始温度，粒子数，密度，步长（时间），步数等）。

（2）体系初始化（初始化粒子的位置坐标的速度）。

（3）计算作用于所有粒子上的力。

（4）解牛顿运动方程。这一步和上一步构成了模拟的核心。重复这两步直至我们计算体系的演化到指定的时间长度。

（5）中心循环完成之后，计算并打印指定体系热力学测定量的平均值，标准差，模拟结束。

这里主要是使用python代码实现，虽然Python相较于C语言执行速度较慢，但是对于以学习为目的而并非以计算模拟实验目的而言编写程序，使用Python进行编码对于初学者来说更为直观，简易，上手起来更快，也更方便在jupyter notebook这样的在线python IDE进行无缝衔接的编码和测试以及运行。

在开始编码前，让我们简单介绍下该程序的基本模型，如下图所示：可视化的展示了分子动学模拟是如何运行的，

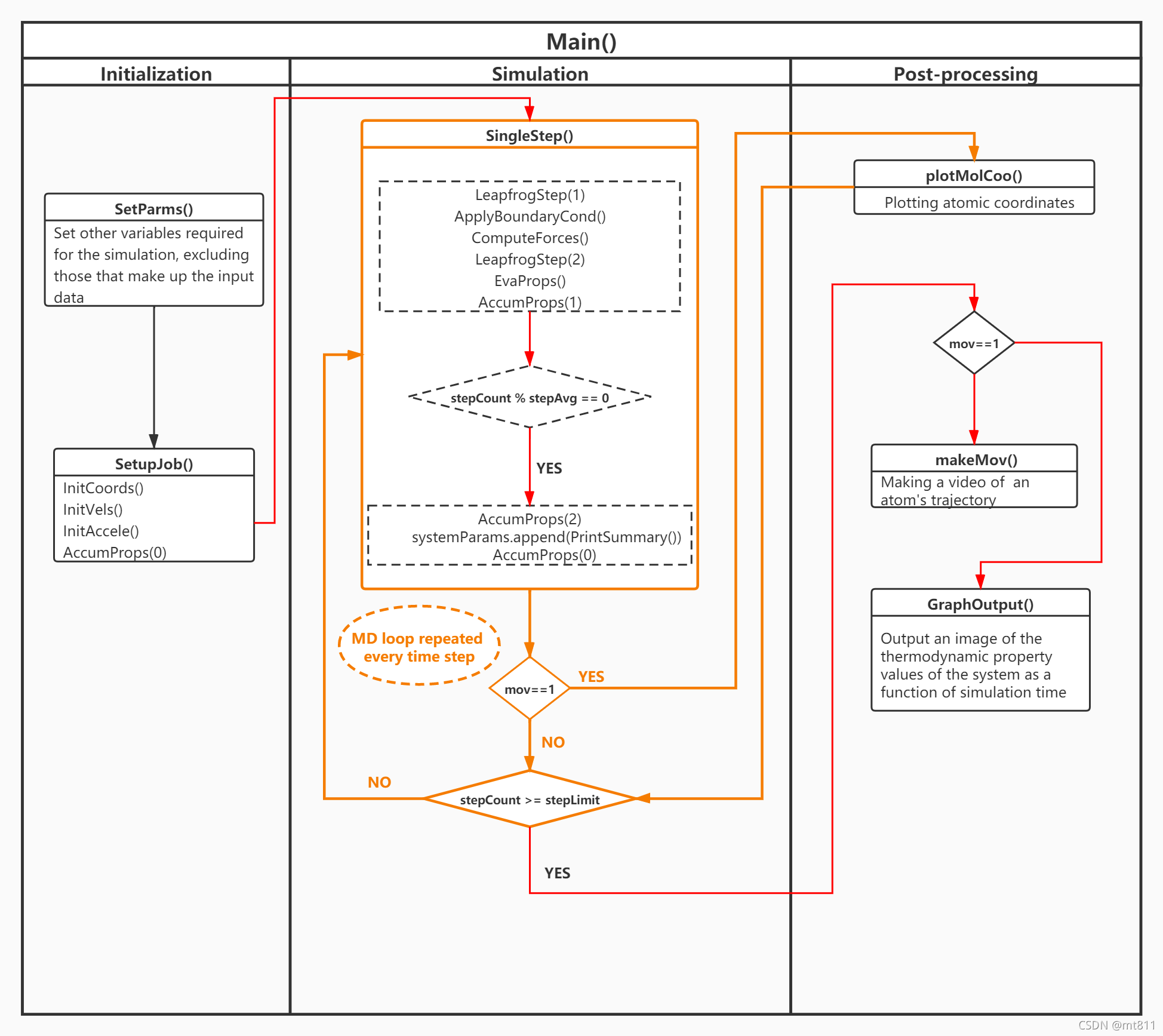
由上图可以知，该主程序（main）主要由三部分组成：Initialzation(位置和速度初始化),Simulation(解粒子运动的方程),Post-processing(后处理，计算测定量)。

这些代有两行方框均代表一个单独的功能函数，其里面由包含了其他的函数（会在接下的编码过程中解释）。该程序的运行的过程如下：

首先,调用SetParams()和SetupJob()函数进行初始化。SetParams()用于设置分子模拟所需的全局变量，而SetupJob()执行InitCoords()，InitVels()和InitAccels()等函数，这分别初始化粒子的坐标，速度和加速度。

其次,进入Simulation,该过程为分子动力学模拟的核心部分，其中SingleStep（）为处理单个时间步长的动力学模拟的行为的函数，其主要功能就是根据粒子的位置、速度和受力计$ \Delta t $?时刻之后粒子的新位置和新速度。它首先调用了LeapFrogStep（）来执行运动方程的积分，再通过ComputeForces（）实现了LJ势和力的计算，并在力的计算中应用了周期性边界条件-ApplyBoundaryCond() ，最后执行两用于属性测量的函数：EvalProps（）和AccumProps（）。反复执行SingleStep（）该过程到直到stepCount变量超过stepLimit。即可结束整个Simulation部分。

最后,Post-processing,其中plotMolCoo（）的功能绘制单个时间步长的模拟体系中粒子的位置分布坐标图像，其数据来源为Simuluation部分通过解牛顿运动方程得到的粒子最新的坐标。而makeMov()为多个时间步长的粒子运动轨迹视频。GraphOutput()为输出模拟体系属性测量值（速度，总能量，动能，压强的均值和标准差）的数据和图像。

下面开始编码，以下每一段代码都会尽可能给出详细解释，部分需要深入了解的前置知识会给出处和参考资料。

3.2 输入文件内容

#输入文件(可自定义):Rap_2_LJP.in
deltaT	0.005      #时间步长
density	0.8       #流体密度
initUcell_x	20   #方格的x大小
initUcell_y	20   #y大小
stepAvg	100       #用来抽样统计步数
stepEquil	0     #平衡步数
stepLimit	500   #模拟循环数
temperature	1.   #温度设置

3.3 代码1 ：运行模拟程序需要导入的依赖包

import pandas as pd
import math
import os
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
from PIL import Image
import glob
import moviepy.editor as mp
from datetime import datetime
import time
import os.path
from os import path
import shutil
from IPython.display import display

“”“
以下这两行是一个魔法函数（Magic Functions）。官方给出的定义是：IPython有一组预先定义好的所谓的魔法函数（Magic Functions），你可以通过命令行的语法形式来访问它们。可见“%matplotlib inline”就是模仿命令行来访问magic函数的在IPython中独有的形式。既然是IPython的内置magic函数，那么在Pycharm中是不会支持的，仅在juypter中有有效，使用.py代码运行则需注释掉。
“”“


#为jupyter notebook中内嵌绘制图像，在代码15中
%matplotlib inline  

#为jupyter notebook中显示pd.DateFrame()显示数据列表，找代码1
from IPython.display import display

3.4 代码2 ：分子类和体系属性类的定义

# 分子类的定义
class Mol():
   def __init__(self,r,rv,ra):
        """
        每一分子对象（mol）所具有的属性如下：
        r:原子坐标
        rv:原子速度
        ra:原子加速度向量
        """
        #初始化以上属性的值
        self.r=np.asarray([0.0,0.0])
        self.rv=np.asarray([0.0,0.0])
        self.ra=np.asarray([0.0,0.0])
        
# 体系属性类，主要用来求体系属性（测定量）的平均值和标准差        
class Prop():
   def __init__(self, val, sum1, sum2 ):
        self.val=val                       #体系测定量的值
        self.sum1=sum1                     #体系测定量的值的和
        self.sum2=sum2                     #体系测定量的值的平方和

3.5 代码3：工具函数

# 返回平方和立方值的函数：
def Sqr(x):
    return (x * x)


def Cube(x):
    return ((x) * (x) * (x))



# 用于生成 (0,1) 范围内的均匀分布的随机数，见18.4
def RandR():
    global randSeedP
    randSeedP=(randSeedP * IMUL + IADD) & MASK
    return (randSeedP*SCALE)

# 用于在二维空间产生具有均匀分布的随机方向的单位向量
def VRand(p):
    s: float
    s = 2. * math.pi * RandR()
    p[0] = math.cos(s)
    p[1] = math.sin(s)
    return p



# 周期性边界（PBC）算法：
"""
第一部分如下：
体系内粒子的坐标的约束：
  二维体系中，一个方形元胞四周有相同的元胞(称为"镜像")，
  若一个粒子从右边边界穿出，操作上左边边界对应位置有相同粒子进入，
  由此保证了元胞中粒子数目即物理量如动量与能量的守恒。
  因此有以下结论：
  region[0]为x方向元胞的边长，则粒子在x方向的坐标区间为：[-0.5*region[0],0.5*region[0]]
  regino[1]为y方向的元胞的边长,则粒子在x方向的坐标区间为：[-0.5*region[1],0.5*region[1]]
  
  以x方向元胞为例：假设边长为1x1的正方形元胞 
  当粒子坐标为x>=0.5时，为了确保当前粒子在一个1x1元胞中，有关系：x-新位置=1，
  故有：新位置=x-1
  同理得： x<-0.5时，有关系：新位置-（x）=1  故有:新位置=1+x，
  
第二部分：对粒子间距离计算使用最小镜像法则，见：ComputerForces()函数
"""
#PBC算法第一部分：对体系内粒子坐标的约束
def VWrapAll(v):
    #对元胞x方向的坐标约束
    if v[0]>=0.5*region[0]:    
        v[0]-=region[0]
    elif v[0]<-0.5*region[0]:
         v[0] +=region[0]
    
    #对元胞y方向的坐标约束
    if v[1] >= 0.5 * region[1]:
        v[1] -= region[1]
    elif v[1] < -0.5 * region[1]:
        v[1] += region[1]
                

3.6 代码4: main()主程序

mov = 1                                      # 如果你想做一个视频的话，设置 mov=1
workdir = str(os.getcwd()+'/')              # 为所有png和视频设置一个工作目录

# 如果/coo目录不存在，就建立它，否则就删除/coo（和它的内容）
# 创建一个新的/coo目录。
if path.exists(str(workdir+'coo'))==False:
    os.makedirs(str(workdir+'coo'))
else:
    shutil.rmtree(str(workdir+'coo'))
    os.makedirs(str(workdir+'coo'))

# 加载输入参数文件
df_params = pd.read_csv('Rap_2_LJP.in', sep='\t', header=None, names=['parameter', 'value'])

#初始该模拟系统热力学属性值
NDIM = 2                        #二维度设置
vSum = np.asarray([0.0, 0.0])   #速度之和
kinEnergy =Prop(0.0, 0.0, 0.0)  #动能
totEnergy =Prop(0.0, 0.0, 0.0)  #势能
pressure  =Prop(0.0, 0.0, 0.0)  #压强

systemParams = []              #初始化系统参数列表

#用于产生随机数算法函数的变量
IADD = 453806245
IMUL = 314159269
MASK = 2147483647
SCALE = 0.4656612873e-9
randSeedP = 17

#初始化参数：把Rap_2_LJP.文件中的参数值传递给MD模拟所需要的相关变量
deltaT = float(df_params.values[0][1])              #模拟步长
density = float(df_params.values[1][1])             #体系密度


initUcell = np.asarray([0.0, 0.0])                 #初始化元胞，具体大小由输入文件密度决定
initUcell[0] = int(df_params.values[2][1])         #元胞X方向长度=20
initUcell[1] = int(df_params.values[3][1])         #元胞X方向长度=20
 
stepAvg = int(df_params.values[4][1])              #抽样平均数
stepEquil = float(df_params.values[5][1])          #平衡步长
stepLimit = float(df_params.values[6][1])          #限制的步数
temperature = float(df_params.values[7][1])        #体系温度

#定义了一个Mol类对象的数组，大小为20*20=400. mol[0]~mol[399]，共400个氩原子分子
mol = [Mol(np.asarray([0.0, 0.0]), \
           np.asarray([0.0, 0.0]), \
           np.asarray([0.0, 0.0])) for i in range(int(initUcell[0]*initUcell[1]))]

global nMol        #定义分子的数量变量
nMol = len(mol)    #为mol数组的长度为400

# 氩-氩相互作用的LJ势参数:
epsilon =  1
sigma = 1

# 执行体系初始化相关功能函数
SetParams()                                   #设置主程序内部模拟所需参数
SetupJob()                                    #初始化粒子的坐标，速度，加速
moreCycles = 1                                #MD循环控制开关变量1：run; 0:stop

n = 0                                        #记录步数，用来给每一步输出的坐标图命名                
while moreCycles:                            #MD循环
    SingleStep()                             #求解每一步的运动方程
    if mov==1:
        plotMolCoo(mol, workdir, n)          #制作单个步长的粒子坐标图
    n += 1
    if stepCount >= stepLimit:
        moreCycles = 0
        
#输出模拟过程中生成的参数
columns = ['timestep','timeNow', '$\Sigma v$', 'E', '$\sigma E$', 'Ek', '$\sigma Ek$', 'P_1', 'P_2']
df_systemParams = pd.DataFrame(systemParams, columns=columns)   

#绘制表格，仅在jupyter notebook使用，打印出数据列表
display(df_systemParams) 

if mov==1:                     
    makeMov()                 # 制作视频
GraphOutput()                 #输出体系测定量随模拟时间变化的图像

3.7 Initilaztion 部分的功能

3.7.1 代码5：steParms()函数

"""
模拟所需的其他变量，不包括那些构成输入数据的变量，
由函数SetParams设置。
"""
def SetParams():
    global rCut    #截断距离
    global region  #区域
    global velMag  #速度变化幅度
    
    #截断值为势阱底部时的原子间距离,即rmin=rCut=2^1/6 *sigma
    rCut=math.pow(2.,1./6. * sigma)
    
    #计算在预设密度条件下，粒子所在区域的大小
    """
    二维空间下的：
    desity=粒子数目/面积，
    平衡体系模拟，密度保持不变，粒子数目不变则需要根据密度来更新粒子活动区域的大小，如下:
    """
    region=np.multiply(1./math.sqrt(density),initUcell) 
    nMol=len(mol)
    
    #速度的变化幅度取决于温度的高低
    velMag = math.sqrt(NDIM * (1. -1. /nMol) * temperature)

3.7.2 代码6：SetupJob()函数

"""
所有初始化计算的工作都集中在以下的函数。
"""
def SetupJob(): 
    global stepCount   #步长计数
    
    stepCount = 0  #初始化步长计数变量的值
    InitCoords()   #初始化坐标
    InitVels()     #初始化速度
    InitAccels()   #初始化加速速度
    AccumProps(0)  #初始化系统属性值（总能量，动能，压强）

代码7 ：InitCoords()，InitVels()，InitAccels()

这里主要是初始化体系粒子的坐标，速度，加速度的函数

# 初始化坐标。
# 这里使用了一个简单的正方形晶格（可以选择不等长的边）,
# 因此，每个元胞只包含一个原子，系统以原点为中心，
def InitCoords():
    c=np.asarray([0.0,0.0])                           #初始坐标值
    gap=np.divide(region,initUcell)                   #单个粒子所在元胞的大小
    n=0                                               #给粒子计数
    
    #将400个原子分别放到元胞中（这些元胞向x,y方向扩胞成了region区域）
    for ny in range(0, int(initUcell[1])):
        for nx in range(0, int(initUcell[0])):
            c = np.asarray([nx+0.5, ny+0.5])
            c = np.multiply(c, gap)
            c = np.add(c, np.multiply(-0.5, region))
            mol[n].r = c
            n=n+1

            
# 初始化速度。
# 初始速度被设置为固定幅度（velMag）,
# 这取决于温度。在分配了随机速度方向后
# 调整速度方向，以确保质心是静止的，因为系统在不受净合外力作用下，其质心速度应该保持不变,
# 函数vRand作为均匀分布的径向单位向量的来源。
def InitVels():
    global vSum
    vSum=np.zeros(vSum.shape)   #返回特定大小，以0填充新的数组:[0,0]，这里是形状
    
    for n in range(nMol):
        VRand(mol[n].rv)                               #产生随机随机速度向量[x,y]
        mol[n].rv=np.multiply(mol[n].rv,velMag)        #根据温度，生成新的速度
        vSum=np.add(vSum,mol[n].rv)                    #质心的速度，系统总速度各质点速度的总和
    
    #调整度方向，以确保质心是静止的,这里取400个粒子在,x,y方向的平均速度1/400*Vsum+每一个原子的速度
    for n in range (nMol):
        mol[n].rv=np.add(mol[n].rv,np.multiply((- 1.0 / nMol),vSum))

        
#初始化加速度。
# 加速度被初始化为零[0,0]
def InitAccels():
    for n in range(nMol):
        mol[n].ra=np.zeros(mol[n].ra.shape)

代码8：AccumProps()

#初始化值
def PropZero(v):
    v.sum1 = v.sum2 = 0.
    return v    
#求和与平方和    
def PropAccum(v):
    v.sum1 += v.val
    v.sum2 += Sqr(v.val)
    return v    

#求平均值和标准差
def PropAvg(v, n):
    v.sum1 /= n
    v.sum2 = math.sqrt(max(v.sum2 / n - Sqr(v.sum1), 0.)) 
    return v 


# AccumProps：收集测定量的结果，并根据要求计算平均值和标准偏差。
def AccumProps(icode):
    
    if icode == 0:             # 0：初始化                                            
        PropZero(totEnergy)
        PropZero(kinEnergy)
        PropZero(pressure) 
    if icode == 1:            # 1：求和                    
        PropAccum(totEnergy)
        PropAccum(kinEnergy)
        PropAccum(pressure)    
    if icode == 2:           # 2：求平均值和标准差
        PropAvg(totEnergy, stepAvg)
        PropAvg(kinEnergy, stepAvg)
        PropAvg(pressure, stepAvg) 

3.8 Simulation 部分功能

该部分有一些关于解分子质心力学体系的运动方程的数值计算方法，还有统计力学中表征体系平衡态热力学属性（能量，压强，温度等）公式和处理方法，均在《The Art of Molecular Dynamics Simulation》第二章，有较为详细的说明，这里在代码中就不在赘述了。

3.8.1 代码9：SingleStep()

def SingleStep():
    
    global stepCount # 步长计数
    global timeNow   #  模拟运行时间

    stepCount +=1                   
    timeNow = stepCount * deltaT    #模拟运行的时间=步数x步长
    LeapfrogStep(1)                #求解运动方程积分
    ApplyBoundaryCond()           #应用周期性边界条件
    ComputeForces()              # 计算原间相互作用力
    LeapfrogStep(2)             # 坐标和速度的积分
    EvalProps()                #计算系统属性值（速度，，速度平方和，总能量，动能，压力）
    AccumProps(1)             #系统属性值求和
    
    #每一百步统计系统的属性值（0,100,200,300,400,500），可以设置stepAvg的值进行自定义
    if (stepCount % stepAvg == 0):
        AccumProps(2)                         #求系统的属性值的平均值和标准差
        systemParams.append(PrintSummary())   #将结果加入到 systemParams列表中
        AccumProps(0)                         # 重置系统属性值用来下一次的统计
          
    

代码10：LeapfrogStep( )

"""
所谓积分方法就是根据粒子的位置，速度和受力计算deltT时刻之后的新位置和新速度算法。
运动方程的积分使用一种简单的数值技术：跃迁法。该方法具有良好的能量守恒特性，
LeapfrogStep整合了坐标和速度。其参数部分决定了两步跃迁过程的哪一部分需要执行。
vix(t + h/2) = vix(t) + (h/2)aix(t)
rix(t + h) = rix(t) + hvix (t + h/2)
"""

def LeapfrogStep(part):
    if part == 1:
        for n in range (nMol):
            mol[n].rv=np.add(mol[n].rv,np.multiply(0.5 * deltaT,mol[n].ra))
            mol[n].r=np.add(mol[n].r,np.multiply(deltaT,mol[n].rv))
    else :
        for n in range(nMol):
            mol[n].rv=np.add(mol[n].rv,np.multiply(0.5 * deltaT,mol[n].ra))

代码11：ApplyBoundaryCond()

# 应用周期性边界，约束粒子坐标位置，保持元胞粒子数恒定 
def ApplyBoundaryCond():
    for n in range(nMol):
        VWrapAll(mol[n].r)

代码12：ComputeForces()

"""
#计算原子间相互作用力函数
ComputeForce函数数：负责根据粒子（原子）的位置计算计算每一个粒子的受力，
由受力情况进而求得加速度。

该函数实现了LJ_force，并计算了位于ri和rj的每一对原子i和j的加速度和力。

rCut=极限分离临界值（rc），它是：rCut=math.pow(2., 1./6.)
当r向rCut增加时，力下降到0。

牛顿第三定律意味着fji=-fij，所以每个原子对只需要检查一次。
"""

def ComputeForces():
    global virSum                    #用于计算压强的中间变量（fij*rij）和
    global uSum                      #LJ势能和
    fcVal=0                          # 原子j对原子i施加的力
    rrCut=Sqr(rCut)                  # rCut:Rc,截断半径的平方
    
    #初始化分子加速度
    for n in range (nMol):
        mol[n].ra=np.zeros(mol[n].ra.shape)
        
    uSum=0.                        #初始化LJ势能和值
    virSum=0.
    n=0
    for j1 in range(nMol-1):
        for j2 in range(j1+1,nMol):
            
            # 使Delta Rij。(RJ1-RJ2的平方之和)
            dr=np.subtract(mol[j1].r,mol[j2].r) # dr包含Rj1和Rj2之间的x,y坐标差值
            VWrapAll(dr)                        #应用PBC约束原子在元胞内,更新了dr[0],dr[1]
            rr=(dr[0] * dr[0] + dr[1] * dr[1]) #两原子距离的平方，这里并未求两原子间距离的绝对值，没必要，因为与截断半径只是比大小，省去了平方根的计算
            r=np.sqrt(rr)                      #r两为原子间的距离     
            
            # 这里是使用原子距离的平方来 dr2 < Rc^2 来判断两原子键相互作用力，
            if(rr < rrCut):
                """
                在原文中：作者认为LJ势尾部的吸引项对该体系模型特征不敏感，所以为了简化计算去掉了
                所以原文有以下代码：
                rri = sigma / rr                 
                rri3 = Cube(rri)
                fcVal = 48. * rri3 * (rri3 - 0.5) * rri
                """
                #本例实现了完整的LJ势能计算，加入了尾部吸引项的描述，所以后续的测定量的计算结果会与原文存在差异
                fcVal = 48 * epsilon * np.power(sigma, 12) / np.power(r, 13) - 24 * epsilon * np.power(sigma, 6) / np.power(r, 7)
               
                # 更新加速度
                mol[j1].ra = np.add(mol[j1].ra, np.multiply(fcVal, dr))
                mol[j2].ra = np.add(mol[j2].ra, np.multiply(-fcVal, dr))
                
                #LJ势能计算
                uSum += 4 * epsilon * np.power(sigma/r, 12)/r - np.power(sigma/r, 6)    
                virSum += fcVal * rr

代码13：EvalProps()

# 计算体系热力学属性值（测定值）
def EvalProps():
    global vSum
    vvSum = 0.                    #系统速度平方的总和
    vSum = np.zeros(vSum.shape)   #质心速度，为系统速度=各质点速度总和，初始化为[0,0]
    
    global kinEnergy                 #动能
    global totEenergy                #总能量
    global pressure                  #压强
    
    #求得质心速度
    for n in range(nMol):
        vSum =np.add(vSum,mol[n].rv)                                        
        vv = (mol[n].rv[0] * mol[n].rv[0] + mol[n].rv[1] * mol[n].rv[1])   #xv^2+yv^2
        vvSum += vv
        
        # 在二维分子体系中，热力学属性值的数值计算方法（见参考书籍第二章）
        kinEnergy.val = (0.5 * vvSum) / nMol                         #单个原子动能，nMol代表原子数
        totEnergy.val = kinEnergy.val + (uSum / nMol)                #总能量：单个原子的动能+单个原子的势能
        pressure.val = density * (vvSum + virSum) / (nMol * NDIM)    #体系压强
        

代码14：PrintSummary( )

# 打印输出体系的测定量
def PrintSummary():
    #打印测定量，保留小数点后四位
    print(stepCount, \
          "{0:.4f}".format(timeNow), \
          "{0:.4f}".format(vSum[0] / nMol) ,\
          "{0:.4f}".format(totEnergy.sum1),\
          "{0:.4f}".format(totEnergy.sum2), \
          "{0:.4f}".format(kinEnergy.sum1), \
          "{0:.4f}".format(kinEnergy.sum2),\
          "{0:.4f}".format(pressure.sum1),\
          "{0:.4f}".format(pressure.sum2))
    
    #返回精确的测定量值
    return (stepCount, \
          timeNow, \
          (vSum[0] / nMol) ,\
          totEnergy.sum1,\
          totEnergy.sum2, \
          kinEnergy.sum1, \
          kinEnergy.sum2,\
          pressure.sum1,\
          pressure.sum2)    

3.9 Post-processing 部分功能

3.9.1 代码15：plotMolCoo( )

# 绘制粒子坐标图
def plotMolCoo(mol,workdir,n):
    import matplotlib.patches as mpatches
    import matplotlib.pyplot as plt
    
    Time=timeNow                                 #模拟时长
    Sigma_v = "{0:.4f}".format(vSum[0] / nMol)
    E = "{0:.4f}".format(totEnergy.sum1)
    Sigma_E = "{0:.4f}".format(totEnergy.sum2)
    Ek = "{0:.4f}".format(kinEnergy.sum1)
    Sigma_Ek = "{0:.4f}".format(kinEnergy.sum2)
    P_1 = "{0:.4f}".format(pressure.sum1)
    P_2 = "{0:.4f}".format(pressure.sum2)  
    
    #该代码能使图表在jupyter notebook中直接显示，在.py代码中不需要
    %matplotlib inline  
    
    TileName = (workdir+'coo/'+str(n)+'.png')      #传入的n表示n步，这里用来给生成的图像命名
    x = []                                         #新建列表保存粒子x的坐标
    y = []                                         #新建列表保存粒子y的坐标
    
    # 遍历0-400号原子的坐标，加入到列表中去
    for n in range(len(mol)):
        x.append(mol[n].r[0])
        y.append(mol[n].r[1])
   
    # 标记400个原子中两个位置较为居中的两相邻原子mol[250]和mol[251],用于观察
    mark_1 = int(len(mol)/2 + len(mol)/8)
    mark_2 = int(len(mol)/2 + len(mol)/8 + 1)
    
    # 根据原子坐标绘制图形
    plt.plot(x, y, 'o', color='blue')                   #每个原子均为蓝色圆形
    plt.plot(x[mark_1], y[mark_1], 'o', color='red')    #标记mark_1为红色
    plt.plot(x[mark_2], y[mark_2], 'o', color='cyan')   #标记mark_2为青色
    
    # 绘制图标的标题
    plt.title('timestep:'+"{0:.4f}".format(timeNow)+'; '+\
              '$\Sigma v$:'+Sigma_v+'; '+\
              'E:'+E+'; '+\
              '$\sigma E$:'+Sigma_E+';\n'+\
              'Ek:'+Ek+'; ' +\
              '$\sigma Ek$:'+Sigma_Ek+'; '+\
              'P.sum1:'+P_1+'; '+\
              'P.sum2:'+P_2+'; ', loc='left')
    
   
    plt.savefig(TileName, dpi=100)                       #保存为坐标图为.png图片

3.9.2 代码16：makeMov ( )

# 制作粒子运动轨迹视频
def makeMov():
    
    # 将多张.png图像转为gif图的片段
    frames = []
    imgs = sorted(glob.glob('coo/*.png'), key=os.path.getmtime)
    for i in imgs:
        temp = Image.open(i)
        keep = temp.copy()
        frames.append(keep)
        temp.close()
        
    # 删除全部的.png图
    for i in imgs:
        os.remove(i)        

    # 片段合并保存为GIF文件，永远循环播放
    frames[0].save('coo/coordinates.gif', format='GIF',
                   append_images=frames[1:],
                   save_all=True,
                   duration=30, loop=0)

    # 将GIF图转换成MP4视频文件
    clip = mp.VideoFileClip("coo/coordinates.gif")
    clip.write_videofile("coo/"+"coordinates"+".mp4")
    
    # 删除gif图
    os.remove("coo/coordinates.gif")

3.9.3 代码17：GraphOutput()

#绘制和系统属性之相关的图像
def GraphOutput():
   
    ax = \
    df_systemParams.plot(x="timestep", y='$\Sigma v$', kind="line")
    df_systemParams.plot(x="timestep", y='E', kind="line", ax=ax, color="C1")
    df_systemParams.plot(x="timestep", y='$\sigma E$', kind="line", ax=ax, color="C2")
    df_systemParams.plot(x="timestep",  y='Ek', kind="line", ax=ax, color="C3")
    df_systemParams.plot(x="timestep", y='$\sigma Ek$', kind="line", ax=ax, color="C4")
    df_systemParams.plot(x="timestep", y='P_1', kind="line", ax=ax, color="C9")
    df_systemParams.plot(x="timestep", y='P_2', kind="line", ax=ax, color="C9")
    
    plt.savefig('plot.jpg', dpi=300)

3.10 完整程序

# 代码1：..........................................................................................
import pandas as pd
import math
import os
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
from PIL import Image
import glob
import moviepy.editor as mp
from datetime import datetime
import time
import os.path
from os import path
import shutil


# 代码2：..........................................................................................
class Mol():
   def __init__(self,r,rv,ra):
        """
        每一分子对象（mol）所具有的属性如下：
        r:原子坐标
        rv:原子速度
        ra:原子加速度向量
        """
        #初始化以上属性的值
        self.r=np.asarray([0.0,0.0])
        self.rv=np.asarray([0.0,0.0])
        self.ra=np.asarray([0.0,0.0])
        
# 体系属性类，主要用来求体系属性（测定量）的平均值和标准差        
class Prop():
   def __init__(self, val, sum1, sum2 ):
        self.val=val                       #体系测定量的值
        self.sum1=sum1                     #体系测定量的值的和
        self.sum2=sum2                     #体系测定量的值的平方和

        
# 代码3：..........................................................................................
def Sqr(x):
    return (x * x)

def Cube(x):
    return ((x) * (x) * (x))

# 用于生成 (0,1) 范围内的均匀分布的随机数，见18.4
def RandR():
    global randSeedP
    randSeedP=(randSeedP * IMUL + IADD) & MASK
    return (randSeedP*SCALE)

# 用于在二维空间产生具有均匀分布的随机方向的单位向量
def VRand(p):
    s: float
    s = 2. * math.pi * RandR()
    p[0] = math.cos(s)
    p[1] = math.sin(s)
    return p

# 周期性边界（PBC）算法：
# PBC算法第一部分：对体系内粒子坐标的约束
def VWrapAll(v):
    #对元胞x方向的坐标约束
    if v[0]>=0.5*region[0]:    
        v[0]-=region[0]
    elif v[0]<-0.5*region[0]:
         v[0] +=region[0]
    
    #对元胞y方向的坐标约束
    if v[1] >= 0.5 * region[1]:
        v[1] -= region[1]
    elif v[1] < -0.5 * region[1]:
        v[1] += region[1]
        
        
# 代码5：..........................................................................................      
def SetParams():
    global rCut    #截断距离
    global region  #区域
    global velMag  #速度幅度
    
    #截断值为势阱底部时的原子间距离,即rmin=rCut=2^1/6 *sigma
    rCut=math.pow(2.,1./6. * sigma)
    region=np.multiply(1./math.sqrt(density),initUcell) 
    nMol=len(mol)
    
    #速度的变化幅度取决于温度的高低
    velMag = math.sqrt(NDIM * (1. -1. /nMol) * temperature)
    
    
# 代码7：..........................................................................................
def InitCoords():
    c=np.asarray([0.0,0.0])                           #初始坐标值
    gap=np.divide(region,initUcell)                   #单个粒子所在元胞的大小
    n=0                                               #给粒子计数
    
    #将400个原子分别放到元胞中（这些元胞向x,y方向扩胞成了region区域）
    for ny in range(0, int(initUcell[1])):
        for nx in range(0, int(initUcell[0])):
            c = np.asarray([nx+0.5, ny+0.5])
            c = np.multiply(c, gap)
            c = np.add(c, np.multiply(-0.5, region))
            mol[n].r = c
            n=n+1
            
            
def InitVels():
    global vSum
    vSum=np.zeros(vSum.shape)   #返回特定大小，以0填充新的数组:[0,0]，这里是形状
    
    for n in range(nMol):
        VRand(mol[n].rv)                               #产生随机随机速度向量[x,y]
        mol[n].rv=np.multiply(mol[n].rv,velMag)        #根据温度，生成新的速度
        vSum=np.add(vSum,mol[n].rv)                    #质心的速度，系统总速度各质点速度的总和
    
    #调整度方向，以确保质心是静止的,这里取400个粒子在,x,y方向的平均速度1/400*Vsum+每一个原子的速度
    for n in range (nMol):
        mol[n].rv=np.add(mol[n].rv,np.multiply((- 1.0 / nMol),vSum))
        
        
def InitAccels():
    for n in range(nMol):
        mol[n].ra=np.zeros(mol[n].ra.shape)
 

# 代码8：..........................................................................................
def PropZero(v):
    v.sum1 = v.sum2 = 0.
    return v    
    
def PropAccum(v):
    v.sum1 += v.val
    v.sum2 += Sqr(v.val)
    return v    

def PropAvg(v, n):
    v.sum1 /= n
    v.sum2 = math.sqrt(max(v.sum2 / n - Sqr(v.sum1), 0.)) 
    return v 


def AccumProps(icode):
    
    if icode == 0:             # 0：初始化                                            
        PropZero(totEnergy)
        PropZero(kinEnergy)
        PropZero(pressure) 
    if icode == 1:            # 1：求和                    
        PropAccum(totEnergy)
        PropAccum(kinEnergy)
        PropAccum(pressure)    
    if icode == 2:           # 2：求平均值和标准差
        PropAvg(totEnergy, stepAvg)
        PropAvg(kinEnergy, stepAvg)
        PropAvg(pressure, stepAvg) 
        
        
# 代码6：..........................................................................................
def SetupJob(): 
    global stepCount   #步长计数
    
    stepCount = 0  #初始化步长计数变量的值
    InitCoords()   #初始化坐标
    InitVels()     #初始化速度
    InitAccels()   #初始化加速度
    AccumProps(0)  #初始化系统属性值（总能量，动能，压强）
    

# 代码10：.........................................................................................
def LeapfrogStep(part):
    if part == 1:
        for n in range (nMol):
            mol[n].rv=np.add(mol[n].rv,np.multiply(0.5 * deltaT,mol[n].ra))
            mol[n].r=np.add(mol[n].r,np.multiply(deltaT,mol[n].rv))
    else :
        for n in range(nMol):
            mol[n].rv=np.add(mol[n].rv,np.multiply(0.5 * deltaT,mol[n].ra))

            
# 代码11：...................................................................................
def ApplyBoundaryCond():
    for n in range(nMol):
        VWrapAll(mol[n].r)
        
# 代码12：...................................................................................
def ComputeForces():
    global virSum                    #用于计算压强的中间变量（fij*rij）和
    global uSum                      #LJ势能和
    fcVal=0                          # 原子j对原子i施加的力
    rrCut=Sqr(rCut)                  # rCut:Rc,截断半径的平方
    
    #初始化分子加速度
    for n in range (nMol):
        mol[n].ra=np.zeros(mol[n].ra.shape)
        
    uSum=0.                        #初始化LJ势能和值
    virSum=0.
    n=0
    for j1 in range(nMol-1):
        for j2 in range(j1+1,nMol):
            
            # 使Delta Rij。(RJ1-RJ2的平方之和)
            dr=np.subtract(mol[j1].r,mol[j2].r) # dr包含Rj1和Rj2之间的x,y坐标差值
            VWrapAll(dr)                        #应用PBC约束原子在元胞内,更新了dr[0],dr[1]
            rr=(dr[0] * dr[0] + dr[1] * dr[1]) #两原子距离的平方，这里并未求两原子间距离的绝对值，没必要，因为与截断半径只是比大小，省去了平方根的计算
            r=np.sqrt(rr)                      #r两为原子间的距离     
            
            # 这里是使用原子距离的平方来 dr2 < Rc^2 来判断两原子键相互作用力，
            if(rr < rrCut):
                fcVal = 48 * epsilon * np.power(sigma, 12) / np.power(r, 13) - 24 * epsilon * np.power(sigma, 6) / np.power(r, 7)
                
                # 更新加速度
                mol[j1].ra = np.add(mol[j1].ra, np.multiply(fcVal, dr))
                mol[j2].ra = np.add(mol[j2].ra, np.multiply(-fcVal, dr))
                
                #LJ势能计算
                uSum += 4 * epsilon * np.power(sigma/r, 12)/r - np.power(sigma/r, 6)    
                virSum += fcVal * rr
                
# 代码13：...................................................................................
def EvalProps():
    global vSum
    vvSum = 0.                    #系统速度平方的总和
    vSum = np.zeros(vSum.shape)   #质心速度，为系统速度=各质点速度总和，初始化为[0,0]
    
    global kinEnergy                 #动能
    global totEenergy                #总能量
    global pressure                  #压强
    
    #求得质心速度
    for n in range(nMol):
        vSum =np.add(vSum,mol[n].rv)                                        
        vv = (mol[n].rv[0] * mol[n].rv[0] + mol[n].rv[1] * mol[n].rv[1])   #xv^2+yv^2
        vvSum += vv
        
        # 在二维分子体系中，热力学属性值的数值计算方法
        kinEnergy.val = (0.5 * vvSum) / nMol                         #单个原子动能，nMol代表原子数
        totEnergy.val = kinEnergy.val + (uSum / nMol)                #总能量：单个原子的动能+单个原子的势能
        pressure.val = density * (vvSum + virSum) / (nMol * NDIM)    #体系压强
        

# 代码14：...................................................................................
def PrintSummary():

    print(stepCount, \
          "{0:.4f}".format(timeNow), \
          "{0:.4f}".format(vSum[0] / nMol) ,\
          "{0:.4f}".format(totEnergy.sum1),\
          "{0:.4f}".format(totEnergy.sum2), \
          "{0:.4f}".format(kinEnergy.sum1), \
          "{0:.4f}".format(kinEnergy.sum2),\
          "{0:.4f}".format(pressure.sum1),\
          "{0:.4f}".format(pressure.sum2))
    
    return (stepCount, \
          timeNow, \
          (vSum[0] / nMol) ,\
          totEnergy.sum1,\
          totEnergy.sum2, \
          kinEnergy.sum1, \
          kinEnergy.sum2,\
          pressure.sum1,\
          pressure.sum2)    

# 代码9：------------------------------------------------------------------------------------------
def SingleStep():
    
    global stepCount # 步长计数
    global timeNow   #  模拟运行时间

    stepCount +=1                   
    timeNow = stepCount * deltaT    #模拟运行的时间=步数x步长
    LeapfrogStep(1)                #求解运动方程积分
    ApplyBoundaryCond()           #应用周期性边界条件
    ComputeForces()              # 计算原间相互作用力
    LeapfrogStep(2)             # 坐标和速度的积分
    EvalProps()                #计算系统属性值（速度，，速度平方和，总能量，动能，压力）
    AccumProps(1)             #系统属性值求和
    
    #每一百步统计系统的属性值（0,100,200,300,400,500），可以设置stepAvg的值进行自定义
    if (stepCount % stepAvg == 0):
        AccumProps(2)                         #求系统的属性值的平均值和标准差
        systemParams.append(PrintSummary())   #将结果加入到 systemParams列表中
        AccumProps(0)                         # 重置系统属性值用来下一次的统计
     

# 代码15：...................................................................................
def plotMolCoo(mol,workdir,n):
    import matplotlib.patches as mpatches
    import matplotlib.pyplot as plt
    
    Time=timeNow                                 #模拟时长
    Sigma_v = "{0:.4f}".format(vSum[0] / nMol)
    E = "{0:.4f}".format(totEnergy.sum1)
    Sigma_E = "{0:.4f}".format(totEnergy.sum2)
    Ek = "{0:.4f}".format(kinEnergy.sum1)
    Sigma_Ek = "{0:.4f}".format(kinEnergy.sum2)
    P_1 = "{0:.4f}".format(pressure.sum1)
    P_2 = "{0:.4f}".format(pressure.sum2)  
    
    
    %matplotlib inline                             
    TileName = (workdir+'coo/'+str(n)+'.png')      #传入的n表示n步，这里用来给生成的图像命名
    x = []                                         #新建列表保存粒子x的坐标
    y = []                                         #新建列表保存粒子y的坐标
    
    # 遍历0-400号原子的坐标，加入到列表中去
    for n in range(len(mol)):
        x.append(mol[n].r[0])
        y.append(mol[n].r[1])
   
    # 标记400个原子中两个位置较为居中的两相邻原子mol[250]和mol[251],用于观察
    mark_1 = int(len(mol)/2 + len(mol)/8)
    mark_2 = int(len(mol)/2 + len(mol)/8 + 1)
    
    # 根据原子坐标绘制图形
    plt.plot(x, y, 'o', color='blue')                   #每个原子均为蓝色圆形
    plt.plot(x[mark_1], y[mark_1], 'o', color='red')    #标记mark_1为红色
    plt.plot(x[mark_2], y[mark_2], 'o', color='cyan')   #标记mark_2为青色
    
    # 绘制图标的标题
    plt.title('timestep:'+"{0:.4f}".format(timeNow)+'; '+\
              '$\Sigma v$:'+Sigma_v+'; '+\
              'E:'+E+'; '+\
              '$\sigma E$:'+Sigma_E+';\n'+\
              'Ek:'+Ek+'; ' +\
              '$\sigma Ek$:'+Sigma_Ek+'; '+\
              'P.sum1:'+P_1+'; '+\
              'P.sum2:'+P_2+'; ', loc='left')
    
    plt.savefig(TileName, dpi=100)                       #保存为坐标图为.png图片
    

# 代码16：...................................................................................
def makeMov():
    
    # 将多张.png图像转为gif图的片段
    frames = []
    imgs = sorted(glob.glob('coo/*.png'), key=os.path.getmtime)
    for i in imgs:
        temp = Image.open(i)
        keep = temp.copy()
        frames.append(keep)
        temp.close()
        
    # 删除全部的.png图
    for i in imgs:
        os.remove(i)        

    # 片段合并保存为GIF文件，永远循环播放
    frames[0].save('coo/coordinates.gif', format='GIF',
                   append_images=frames[1:],
                   save_all=True,
                   duration=30, loop=0)

    # 将GIF图转换成MP4视频文件
    clip = mp.VideoFileClip("coo/coordinates.gif")
    clip.write_videofile("coo/"+"coordinates"+".mp4")
    
    # 删除gif图
    os.remove("coo/coordinates.gif")
    

# 代码17：...................................................................................
def GraphOutput():
   
    ax = \
    df_systemParams.plot(x="timestep", y='$\Sigma v$', kind="line")
    df_systemParams.plot(x="timestep", y='E', kind="line", ax=ax, color="C1")
    df_systemParams.plot(x="timestep", y='$\sigma E$', kind="line", ax=ax, color="C2")
    df_systemParams.plot(x="timestep",  y='Ek', kind="line", ax=ax, color="C3")
    df_systemParams.plot(x="timestep", y='$\sigma Ek$', kind="line", ax=ax, color="C4")
    df_systemParams.plot(x="timestep", y='P_1', kind="line", ax=ax, color="C9")
    df_systemParams.plot(x="timestep", y='P_2', kind="line", ax=ax, color="C9")
    
    plt.savefig('plot.jpg', dpi=300)
    
    
# 代码3：************************************Main************************************************
mov = 1                                      # 如果你想做一个视频的话，设置 mov=1
workdir = str(os.getcwd()+'/')              # 为所有png和视频设置一个工作目录

if path.exists(str(workdir+'coo'))==False:
    os.makedirs(str(workdir+'coo'))
else:
    shutil.rmtree(str(workdir+'coo'))
    os.makedirs(str(workdir+'coo'))

# 加载输入参数文件
df_params = pd.read_csv('Rap_2_LJP.in', sep='\t', header=None, names=['parameter', 'value'])

#初始该模拟系统热力学属性值
NDIM = 2                        #二维度设置
vSum = np.asarray([0.0, 0.0])   #速度之和
kinEnergy =Prop(0.0, 0.0, 0.0)  #动能
totEnergy =Prop(0.0, 0.0, 0.0)  #势能
pressure  =Prop(0.0, 0.0, 0.0)  #压强

systemParams = []              #初始化系统参数列表

#用于产生随机数算法函数的变量
IADD = 453806245
IMUL = 314159269
MASK = 2147483647
SCALE = 0.4656612873e-9
randSeedP = 17

#初始化参数：把Rap_2_LJP.文件中的参数值传递给MD模拟所需要的相关变量
deltaT = float(df_params.values[0][1])              #模拟步长
density = float(df_params.values[1][1])             #体系密度


initUcell = np.asarray([0.0, 0.0])                 #初始化元胞，具体大小由输入文件密度决定
initUcell[0] = int(df_params.values[2][1])         #元胞X方向长度=20
initUcell[1] = int(df_params.values[3][1])         #元胞X方向长度=20
 
stepAvg = int(df_params.values[4][1])              #抽样平均数
stepEquil = float(df_params.values[5][1])          #平衡步长
stepLimit = float(df_params.values[6][1])          #限制的步数
temperature = float(df_params.values[7][1])        #体系温度

#定义了一个Mol类对象的数组，大小为20*20=400. mol[0]~mol[399]，共400个氩原子分子
mol = [Mol(np.asarray([0.0, 0.0]), \
           np.asarray([0.0, 0.0]), \
           np.asarray([0.0, 0.0])) for i in range(int(initUcell[0]*initUcell[1]))]

global nMol        #定义分子的数量变量
nMol = len(mol)    #为mol数组的长度为400

# 氩-氩相互作用的LJ势参数:
epsilon =  1
sigma = 1

# 执行体系初始化相关功能函数
SetParams()                                   #设置主程序内部模拟所需参数
SetupJob()                                    #初始化粒子的坐标，速度，加速
moreCycles = 1                                #MD循环控制开关变量1：run; 0:stop

n = 0                                        #记录步数，用来给每一步输出的坐标图命名                
while moreCycles:                            #MD循环
    SingleStep()                             #求解每一步的运动方程
    if mov==1:
        plotMolCoo(mol, workdir, n)          #制作单个步长的粒子坐标图
    n += 1
    if stepCount >= stepLimit:
        moreCycles = 0
        
#输出模拟过程中生成的参数
columns = ['timestep','timeNow', '$\Sigma v$', 'E', '$\sigma E$', 'Ek', '$\sigma Ek$', 'P_1', 'P_2']
df_systemParams = pd.DataFrame(systemParams, columns=columns)    

#绘制表格，仅在jupyter notebook使用，打印出数据列表
display(df_systemParams)

if mov==1:                     
    makeMov()                 # 制作视频
GraphOutput()                 #输出体系测定量随模拟时间变化的图像

3.11 运行程序代码步骤：

以下过程均能在搜索引擎中简单解决，这里不再赘述

1. 安装python 3
2. 安装程序运行所需的依赖包（在代码1中已经给出，已存在的无需安装，可自己搜索相关国内镜像资源包安装更块）
3. 在以下文件夹中运行程序：
   （可选）安装装jupyter notebook在线运行，也可以在本地命令行（shell或dos）中运行

├── configura                    :运行该分子动力学模拟配置文件
│   ├── Rap_2_LJP.in            :运行模拟需要输出的参数文件
│   ├── MD_LJP.py               :在shell或dos）中运行的程序
│   └── MD_LJP.ipynb            :jupyter notebook中运行的程序 

4. 开始运行

• 方式1：在命令行中运行,命令如下

python MD_ljp.py

• 方式2：jupyter notebook中运行
  步骤如下：
  • (1).在MD_LJP.ipynb 所在文件夹中启动jupyter notebook
  • (2).打开MD_LJP.ipynb文件，点击“运行”按钮即可

5. 结果：
   例如：在 configura文件夹下运行模拟程序，会新增以下下文件：（整过程大概六分钟左右，我的电脑配置较差了）

├── configura
│   ├── coo                     :保存模拟轨迹视频的文件夹 (新增)
         ├──coordinates.mp4      :MP4格式的模拟轨迹视频 (新增)
│   ├── plot.png                :模拟体系测定量随模拟时间变化的图像。(新增)
│   ├── Rap_2_LJP.in            :运行模拟需要输出的参数文件
│   ├── MD_LJP.py               :在shell或dos）中运行的程序
│   └── MD_LJP.ipynb            :jupyter notebook中运行的程序 

在jupyter notebook中输出以下内容，如图所示：

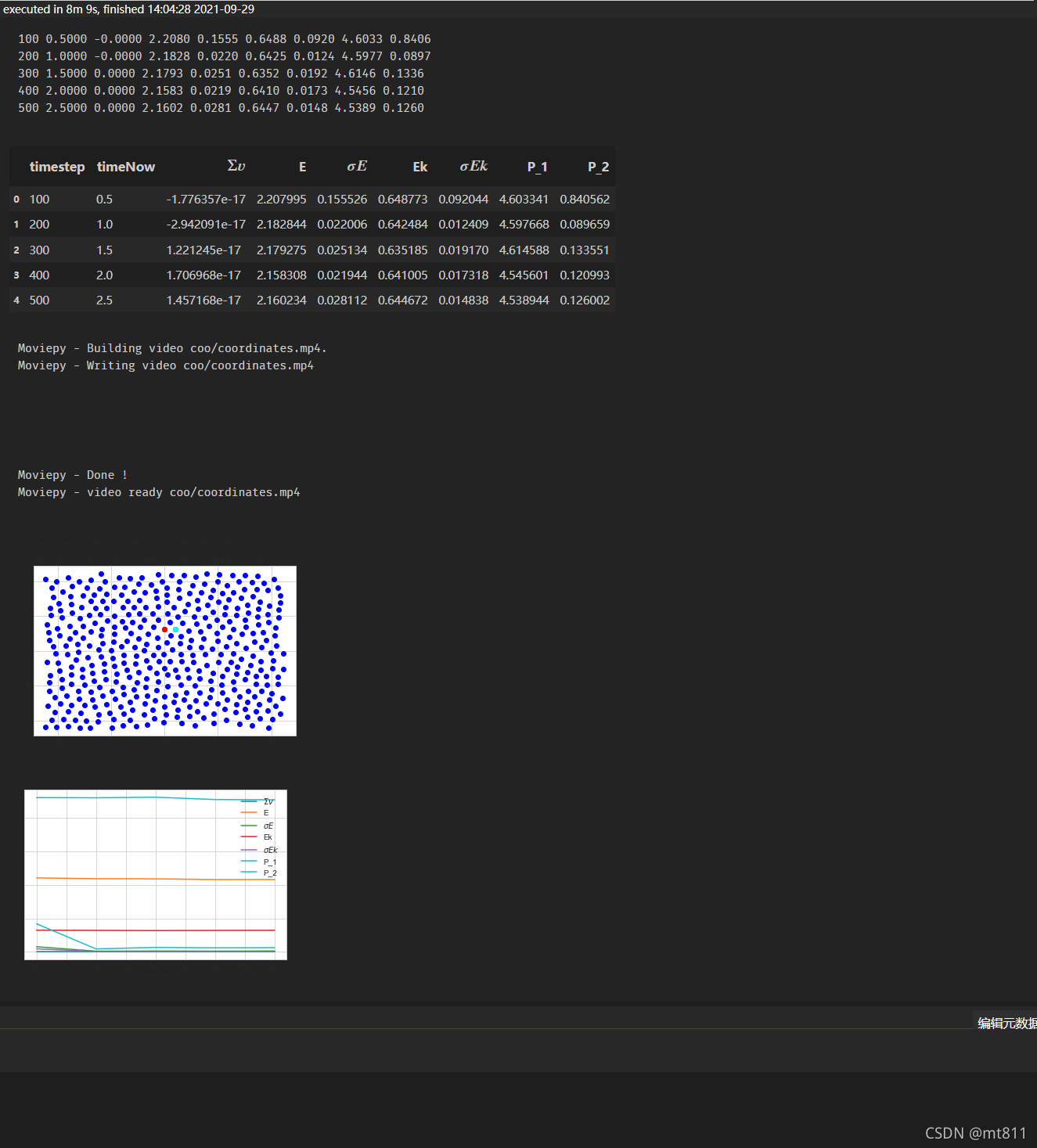
4. reference

1. 分子模拟和物理相关理论

• Daan Frenkel 《Understanding Molecular Simulation：From Algorithms to Applications Second Edition》

• 译版 《分子间相互作用——物理图像，计算方法与模型势能》

2. 分子模拟编程实践

   • D.C RAPAPORT 《The Art of Molecular Dynamics Simulation 2th》 本文程序主要参考本书第二章节

   • 链接：lennard-jones-potential

3. python编程与数据分析

• 《Python编程：从入门到实践》（第二版）

• 《Python数据科学手册》

5. 最后

对于初学者来说无论是分子模拟里面的基础理论和计算方法，还是编程实现，最重要的是从全局入手，建立直觉，至于细节可以实践中去学习，需要再去深入。因此本文对分子模拟相关知识均只是略有介绍，更多系统的细节知识请参考本文以上列出的书籍和文献。关注公众号“理论与计算化学初学者” 回复关键词"MD_LJP" 即可获得相关参考资料，模拟程序以及运行示例文件。