[人工智能]因子分析——附数据下载

因子分析的主要目的是用来描述隐藏在一组测量到的变量中的一些更基本的，但又无法直接测量到的隐性变量 。与主成分分析相似，因子分析也具有降维的功能，但与主成分分析不同之处在于，因子分析是对主成分分析的扩展，提取出的公因子不仅考虑变量之间的相关性，还考虑了变量之间相关性的强弱，因此更容易解释其代表的含义。
本文从网络上搜集了三个案例，对这些案例进行了整理，主要目的是为了说明因子分析的步骤，更容易看懂。数据下载在此（一个工作表是一份数据）
因子分析步骤：
（1）数据导入，进行KMO和Bartlett球形检验，判断是否适合做因子分析
（2）若数据适合做因子分析，若未知因子数目，首先做探索性因子分析，做碎石图，判断提取因子个数；若已知问卷测量的变量数目，则可以先做探索性因子分析，再做验证性因子分析，利用热力图判断变量测量是否准确
（3）若需要利用因子分析计算排序结果，则先计算因子得分，再根据因子得分与样本数据在各因子上的表现，综合计算得出排序结果。

案例1：问卷数据的探索性因子分析和验证性因子分析
这是一份已知有25个测量题目的问卷，测量的变量是5个，认同性agree;勤奋的, 责任感conscientious;外向的extraversion;神经质, 不稳定性neuroticism;开放性openness。
现在我们假设不知道是5个变量，验证其问卷的有效性。
首先导入数据：

import pandas as pd
dt=pd.read_excel(r'因子分析数据.xlsx',sheet_name='问卷数据')
dt.head(2)

数据如下图：

可以看到，在这个数据中，有一些列是我们不需要的，要把它去除：

dt1=dt.drop(['Unnamed: 0','gender','education','age'],axis=1)
dt1.head(2)

去除后的数据如下：

接着，查看数据是否存在缺失值，对缺失数据进行删除：

dt1.isnull().sum()

发现数据是有缺失值的，于是删除存在缺失值的数据，再查看数据量：

dt1.dropna(inplace=True)
dt1.shape

(2436, 25)
还剩余2436条数据，样本量足够大。
下面首先做KMO和Bartlett检验：
引入所需要的包，这个factor_analyzer包得提前去安装

from factor_analyzer import FactorAnalyzer
from factor_analyzer.factor_analyzer import calculate_kmo
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity

计算出相应的KMO和Bartlett检验结果：

kmo_all,kmo_model=calculate_kmo(dt1)
chi_square_value,p_value=calculate_bartlett_sphericity(dt1)
print('kmo_all:',kmo_all)
print('kmo_model',kmo_model)
print('chi_square_value',chi_square_value)
print('p_value',p_value)

结果为：
可以看到，每个问题的KMO统计量都大于0.75，算是不错的结果了，一般最差大于0.5就可以用，而总的KMO达到了0.8485，同时p值为0，表明问卷的基本数据效度不错。
在假定不知道是5个变量的情况下，先做探索性因子分析，看看提取几个公因子比较合适，并计算出特征值

fa=FactorAnalyzer(10,rotation=None)
fa.fit(dt1)
ev,v=fa.get_eigenvalues()

然后绘制碎石图：

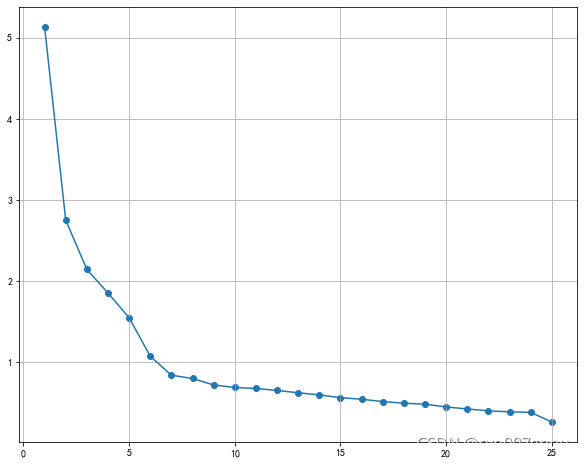
按取特征值大于1的要求来看，确实5个公因子更为合适，但实际操作时并不完全根据图形判断，还需要借助累计方差贡献率，一般达到85%左右即可，但这份数据确实有些问题，累计方差贡献率较低，后面在热力图上也有表现。
输出特征值，方差贡献率和累计方差贡献率：

fa_v = fa.get_factor_variance()
fa_dt = pd.DataFrame(
        {'特征值': fa_v[0], '方差贡献率': fa_v[1], '方差累计贡献率': fa_v[2]})
    #各个因子的方差以及方差贡献率
print("\n",fa_dt)

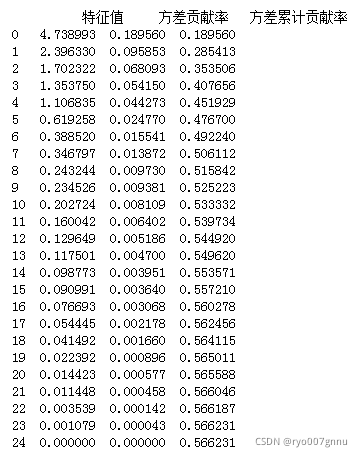
只有5个特征值大于1的，于是按5个公因子，做因子旋转，再次拟合

fa = FactorAnalyzer(rotation='varimax', n_factors=5, method='principal')
fa.fit(dt1)

再次输出结果：

fa_v = fa.get_factor_variance()
fa_dt = pd.DataFrame(
        {'特征值': fa_v[0], '方差贡献率': fa_v[1], '方差累计贡献率': fa_v[2]})
    #各个因子的特征值以及方差贡献率
print("\n",fa_dt)

可以看出，这个方差累计贡献率确实不高。再来进行验证性因子分析，绘制热力图：

import seaborn as sns
dt2=pd.DataFrame(np.abs(fa.loadings_),index=dt1.columns)
plt.figure(figsize=(10,8))
ax=sns.heatmap(dt2,annot=True,cmap='BuPu')#这个cmap是指颜色区间，BuPu是一种颜色的范围，大致是由灰变紫
plt.show()

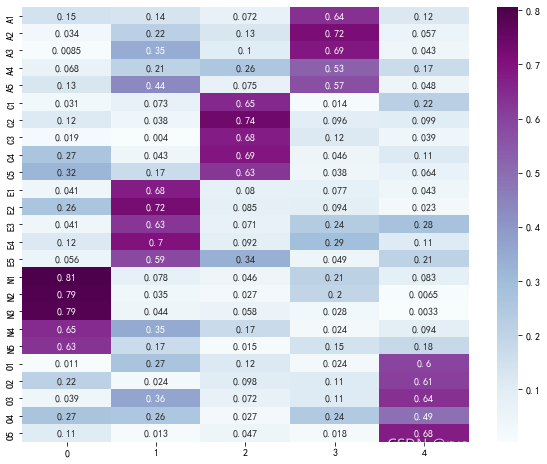
可以看到，基本上所有的载荷较高的在同一编码下（如C1，C2，C3）的基本都在一个因子下（如第3列），表明问卷的效度较好。但这里的数据也可以看到，有的项值并没有大于0.5，按要求至少应该超过0.5的。
至此，我们对该数据探索性因子分析认为应该是5个因子，同时进行验证性因子分析也确定是5个因子，问卷效度基本达标。

案例2：成绩数据的文理偏科情况分析
这是一份包含近600条记录的学生成绩（看上去好像是初中的），对该数据进行因子分析，判断是否存在文理偏科的情况？
还是一样，先导入数据，去除多余列：

dt=pd.read_excel(r'因子分析数据.xlsx',sheet_name='成绩数据')
dt.head(2)

学号，班级和体育（一般没人拿它来分科）是多余列，删去：

dt1=dt.drop(['学号','班级','体育'],axis=1)

经过判断没有缺失值，可以继续下一步了，先进行KMO和Bartlett检验：
代码和上面的例子一样：

from factor_analyzer import FactorAnalyzer
from factor_analyzer.factor_analyzer import calculate_kmo
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
kmo_all,kmo_model=calculate_kmo(dt1)
chi_square_value,p_value=calculate_bartlett_sphericity(dt1)
print('kmo_all:',kmo_all)
print('kmo_model',kmo_model)
print('chi_square_value',chi_square_value)
print('p_value',p_value)

同样，数据的KMO和Bartlett检验均通过，适合做因子分析。
还是先做探索性因子分析，绘制碎石图，并输出特征值等数据：

fa=FactorAnalyzer(9,method='principal',rotation=None)
fa.fit(dt1)
ev,v=fa.get_eigenvalues()

from matplotlib import pyplot as plt
plt.figure(figsize=(10,8))
plt.scatter(range(1,dt1.shape[1]+1),ev)
plt.plot(range(1,dt1.shape[1]+1),ev)
plt.grid(True)
plt.show()

fa_v = fa.get_factor_variance()
fa_dt = pd.DataFrame(
        {'特征值': fa_v[0], '方差贡献率': fa_v[1], '方差累计贡献率': fa_v[2]})
    #各个因子的方差以及方差贡献率
print("\n",fa_dt)

碎石图如下：

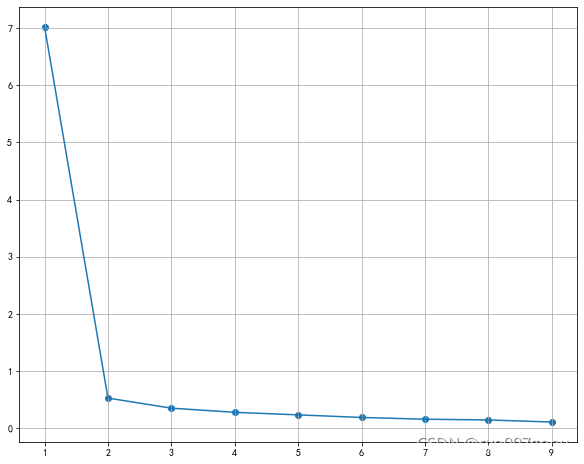
特征值、方差贡献率、累计方差贡献率如下：

看上去1个公因子就差不多了，不过在这个环境下，既然是否偏科，我们就还是按文理科的思路去折腾吧，还是提取2个公因子。
和上面的步骤相同，再次进行因子旋转拟合：

#取方差解释率接近0.85时共2个因子，因子旋转后再次拟合
fa = FactorAnalyzer(rotation='varimax', n_factors=2, method='principal')
fa.fit(dt1)

绘制热力图：

import seaborn as sns
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
dt2=pd.DataFrame(np.abs(fa.loadings_),index=dt1.columns)
plt.figure(figsize=(10,8))
ax=sns.heatmap(dt2,annot=True,cmap='BuPu')
plt.show()

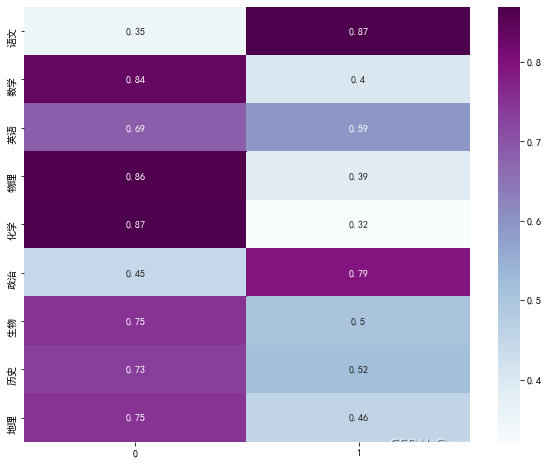
可以看到，只有语文和政治在第2个因子（F2）上较大，而其他科目则在第1个因子（F1）上较大，暂且把第2个因子称为文科因子，第1个因子称为理科因子。语文就可以表示为0.35F1+0.87F2。
根据我的理解，在初中阶段，基本也看不出什么文理科差距，不过有些语文和政治相关，数学和物理、化学相关，这些大家还是能理解的。在英语上，好像理科学得好的，英语也很不错。
然后对所有的学生做热力图：

dt2=fa.transform(dt1)
ax=sns.heatmap(dt2,annot=True,cmap='BuPu')
plt.show()

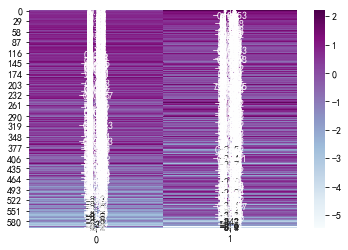
可以看到几乎都是紫色的，也差不多可以认为，大多数的同学都偏理科了。
假设有个学生的分数是[130,108,120,67.2,48.25,50,48.5,47.5,47]
我们将其代入，计算因子系数：

fa.transform(pd.DataFrame([[130,108,120,67.2,48.25,50,48.5,47.5,47]]))

结果为：array([[-0.98165912, 4.00093525]])
可以看出，这个同学在第2个因子上表现更为突出，严重偏文科？？？

案例3：应聘者选择的因子分析
数据是一个单位对48名应聘者的问卷数据的收集，现在该单位想通过这份数据录取其中6名最优者，该如何进行？

依旧是先导入数据，去除多余列：

dt=pd.read_excel(r'因子分析数据.xlsx',sheet_name='应聘者数据')
dt1=dt.drop('ID',axis=1)
dt1.head(2)

数据如下：

老规矩，先做KMO和Bartlett检验：

#做KMO和Bartlett检验
from factor_analyzer.factor_analyzer import calculate_kmo
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
kmo_all,kmo_model=calculate_kmo(dt1)
chi_square_value,p_value=calculate_bartlett_sphericity(dt1)
print(kmo_all)
print(kmo_model)
print(chi_square_value)
print(p_value)

貌似总体还行，有个别的不太好。
做探索性因子分析：
绘制碎石图及计算特征值等：

#做探索性因子分析
fa = FactorAnalyzer(rotation=None, n_factors=15, method='principal')
fa.fit(dt)
ev,v=fa.get_eigenvalues()
plt.figure(figsize=(10,8))
plt.scatter(range(1,dt.shape[1]+1),ev)
plt.plot(range(1,dt.shape[1]+1),ev)
plt.show()

fa_v = fa.get_factor_variance()
fa_dt = pd.DataFrame(
        {'特征值': fa_v[0], '方差贡献率': fa_v[1], '方差累计贡献率': fa_v[2]})
    #各个因子的特征值以及方差贡献率
fa_dt

看上去4个公因子就行，但我们还是按累计贡献率85%以上，选择5个公因子再次做拟合。

#取方差解释率大于0.85时共5个因子，因子旋转后再次拟合
fa = FactorAnalyzer(rotation='varimax', n_factors=5, method='principal')
fa.fit(dt1)

对每位应聘者按因子得分进行计算分值：

#计算得分
def F(factors):  
    return sum(factors*fa.get_factor_variance()[1])
scores = []  
for i in range(len(fa.transform(dt1))):  #这个fa.transform(dt1)就是各应聘者的因子得分，再乘以对应的因子贡献率所占的权重，计算出总得分
    new = F(fa.transform(dt1)[i])  
    scores.append(new)  
print(scores)

对所有应聘者按得分进行排序：

dt['scores']=scores
dt.scores.sort_values(ascending=False)

可以看到，39、38、7、9、6和22号应聘者是该单位要录取的人。
做个图看看：

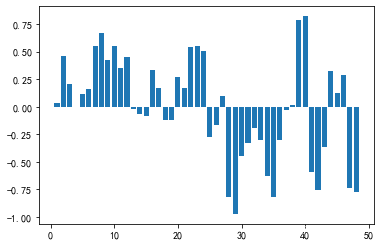
不过这个题我做的结果和网上的不太一样，不知道是数据的问题，还是哪里出了问题，还请大家指出。
好了，3个案例全部说完，收工。