奇异谱分析SSA
这两个月跟着老师做项目,接触了一点时间序列分析和预测的内容,主要是基于矩阵分解的奇异谱分析(Singular Spectrum Analysis,SSA),趁国庆放假,整理一下做个笔记。
SSA (Singular Spectrum Analysis)
奇异谱分析(SSA)是一种处理非线性时间序列数据的方法,可以对时间序列进行分析和预测。它基于构造在时间序列上的特定矩阵的奇异值分解(SVD),可以从一个时间序列中分解出趋势、振荡分量和噪声。SSA具有非常广泛的适用性,对于时间序列,既不需要假设参数模型,也不需要假设平稳性条件。
SSA算法的基本流程
考虑一个长度为N的时间序列
X
?
=
X
N
?
=
(
x
1
,
…
,
x
N
)
X^·=X^·_N=(x_1,…,x_N)
X?=XN??=(x1?,…,xN?)。
N
>
2
N> 2
N>2,且
X
X
X是一个非零序列,即,至少存在一个
i
i
i使得
x
i
≠
0
x_i \neq0
xi??=0。令整数
L
(
1
<
L
<
N
)
L(1<L<N)
L(1<L<N)为窗口长度,且
K
=
N
L
+
1
K=N_L+1
K=NL?+1
SSA算法的过程由分解和重构两个互补的阶段组成。
分解
- 第一步 嵌入
我们将原始时间序列映射成一个长度为 L L L的向量序列,形成 K = N ? L + 1 K =N?L+1 K=N?L+1个长度为 L L L的向量:
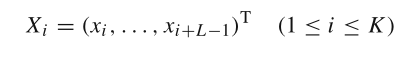
这些向量组成轨迹矩阵:

- 第二步:奇异值分解
在这一步,对轨迹矩阵 X X X进行奇异值分解(SVD)。令 S = X X T S=XX^T S=XXT, λ 1 , . . . , λ L λ_1,...,λ_L λ1?,...,λL?为 S S S的特征值,且 λ 1 ≥ . . . ≥ λ L ≥ 0 λ_1≥...≥λ_L≥0 λ1?≥...≥λL?≥0;而 U 1 , . . . , U L U_1,...,U_L U1?,...,UL?是矩阵 S S S对应于这些特征值的标准正交向量。
令 d = r a n k ( X ) = m a x { i , λ i > 0 } d=rank(X)=max\{i,λ_i>0\} d=rank(X)=max{i,λi?>0}(注意,在实际序列中,我们通常有 d = L ? , L ? = m i n { L , K } d=L^?,L^?=min\{L,K\} d=L?,L?=min{L,K})。 V i = X T U i / λ i ( i = 1 , … , d ) V_i =X^TU_i/\sqrt{ λ_i}(i=1,…,d) Vi?=XTUi?/λi??(i=1,…,d)
这种情况下,轨迹矩阵 X X X的SVD可以写成:
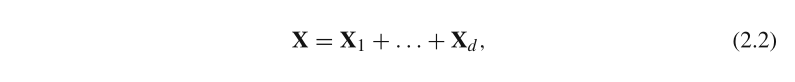
其中, X i = λ i U i V i T X_i =\sqrt{ λ_i}U_iV_i^T Xi?=λi??Ui?ViT?
重构
-
第三步 分组(grouping)
先将下标集合 { 1 , . . . , d } \{1,...,d\} {1,...,d}划分成 m m m个互不相交的子集 I 1 , . . . I m I_1,...I_m I1?,...Im?,令 I = { i 1 , . . . , i p } I=\{i_1,...,i_p\} I={i1?,...,ip?},则对应于 I I I的合成矩阵 X I = X i 1 + . . . + X i p X_I=X_{i_1}+...+X_{i_p} XI?=Xi1??+...+Xip??。则有:
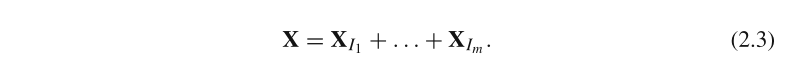
-
第四步:对角线平均
在这一步中,我们将(2.3)中的每个矩阵 X I j X_{I_j} XIj??变换为一个长度为N的新序列,即得到分解后的序列。令 Y Y Y为一个 L ? K L*K L?K的矩阵,元素为 y i j , 1 ≤ i ≤ L , 1 ≤ j ≤ K . y_{ij},1≤i≤L, 1≤j≤K. yij?,1≤i≤L,1≤j≤K.令 L ? = m i n ( L , K ) , K ? = m a x ( L , K ) , N = L + K ? 1 L^?=min(L,K),K^?=max(L,K),N=L+K?1 L?=min(L,K),K?=max(L,K),N=L+K?1.如果 L < K L< K L<K, y i j ? = y i j y^?_{ij} = y_{ij} yij??=yij?,否则, y i j ? = y j i y^*_{ij} = y_{ji} yij??=yji?
我们利用下面的公式2.4进行对角线求平均,将矩阵 Y Y Y转换为序列 y 1 , … , y N y_1,…, y_N y1?,…,yN?

即根据下图所示对角线求平均,将二维矩阵转换为一维序列:

SSA预测
SSA的预测,可以简单理解为一种线性递归过程,即:
y N + 1 = a 1 y N + a 2 y N ? 1 + . . . + a L ? 1 y N ? L + 1 y_{N+1}=a_1y_{N}+a_2y_{N-1}+...+a_{L-1}y_{N-L+1} yN+1?=a1?yN?+a2?yN?1?+...+aL?1?yN?L+1?
其中,系数 a 1 , . . . a L ? 1 a_1,...a_{L-1} a1?,...aL?1?根据SVD获得的特征值计算得到。
SSA的预测方法有递归(recurrent)和矩阵(vector)两种。
Recurrent Forecast
时间序列
Y
N
+
M
=
(
y
1
,
.
.
.
,
y
N
+
M
)
Y_{N+M}=(y_1,...,y_{N+M})
YN+M?=(y1?,...,yN+M?)的递归预测公式如下:
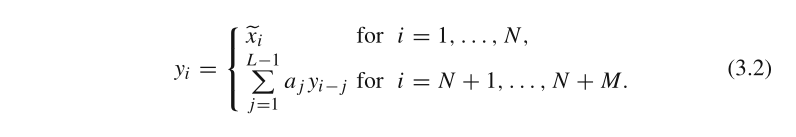
其中,
x
i
~
为
根
据
公
式
2.4
重
构
出
来
的
时
间
序
列
值
。
\tilde{x_i}为根据公式2.4重构出来的时间序列值。
xi?~?为根据公式2.4重构出来的时间序列值。
y
N
+
1
,
.
.
.
,
y
N
+
M
y_{N+1},...,y_{N+M}
yN+1?,...,yN+M?为M个预测值。
则,我们只需要求出系数
a
1
,
.
.
.
a
L
?
1
a_1,...a_{L-1}
a1?,...aL?1?即可。计算方法如下:
记向量
R
=
(
a
L
?
1
,
.
.
.
,
a
1
)
T
R=(a_{L?1},...,a_1)^T
R=(aL?1?,...,a1?)T,且有
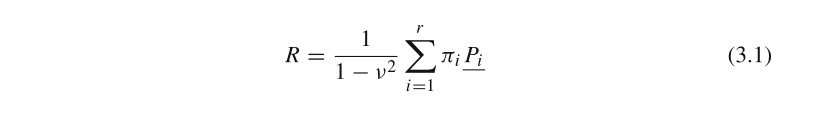
式3.1中,
ν
2
=
π
1
2
+
.
.
.
+
π
r
2
\nu^2=\pi_1^2+...+\pi_r^2
ν2=π12?+...+πr2?;
π
i
\pi_i
πi?是向量
P
i
(
i
=
1
,
.
.
.
,
r
)
P_i(i=1,...,r)
Pi?(i=1,...,r)的最后一个分量,
P
i
P_i
Pi?则是在SVD分解过程中得到的标准正交向量。
Vector Forecast
SSA预测的另一种方法是向量预测法。总的来说,向量预测比递归预测更稳定,特别是当序列中异常值较多的时候。考虑下面的矩阵:
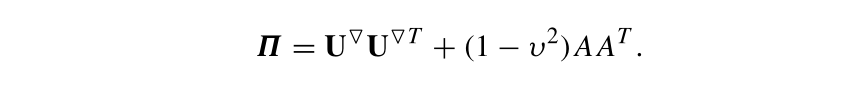
定义线性算子如下:

其中,
Y
Δ
Y_\Delta
YΔ?是
Y
Y
Y的后
L
?
1
L-1
L?1个元素构成的向量。定义向量
Z
j
Z_j
Zj?如下:
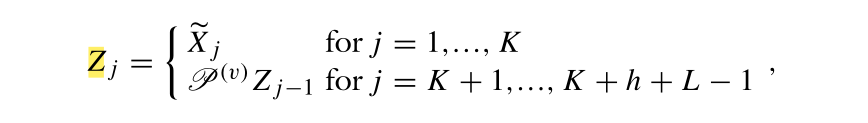
其中,
X
j
~
\tilde{X_j}
Xj?~?为轨迹矩阵经过分组并剔除噪声分量后重构的第
j
j
j列。现在,通过构造矩阵
Z
=
[
Z
1
,
.
.
.
,
Z
K
+
h
+
L
?
1
]
Z=[Z_1,...,Z_{K+h+L-1}]
Z=[Z1?,...,ZK+h+L?1?],并进行对角线平均,可以得到一个新的序列
y
^
1
,
.
.
.
,
y
^
K
+
h
+
L
?
1
\hat{y}_1,...,\hat{y}_{K+h+L-1}
y^?1?,...,y^?K+h+L?1?,其中,
y
^
N
+
1
,
.
.
.
,
y
^
N
+
h
\hat{y}_{N+1},...,\hat{y}_{N+h}
y^?N+1?,...,y^?N+h?则是通过Vector方法获得预测值。
Vector方法预测过程如下图所示:

python实现
SSA的代码实现,还是比较多的,基本上都是实现了分解和重构,预测一般也都是recurrent方法,如
pyts中的SSA
GitHub上也有比较多:
pssa
ssa-py
我基于GitHub上面的pssa,修改了一下,粗略实现了vector预测方法,有空的时候再整理传到GitHub吧。