代码实现西瓜分类,我们先上数据:
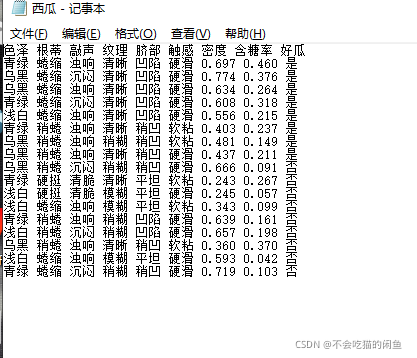
我的编程实现过程非常杂糅,没有系统,而且我的python也没学多久,所以用的都是简单的循环、函数。在编程过程中,我把色泽变量记为x1,根蒂记为x2,敲声记为x3,纹理记为x4,脐部记为x5,触感记为x6,密度记为x7,含糖率记为x8,是否为好瓜这一名义变量记好瓜为0,坏瓜为1。
接下来,我们引入一些有关朴素贝叶斯算法的基础知识:
首先是计算先验概率:
在实际编程过程中我直接使用拉普拉斯平滑,取
λ
=
1
\lambda=1
λ=1
则先验概率为
P λ ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) + λ N + K λ \\P_\lambda(Y=c_k) = \frac{\sum_{i=1}^NI(y_i=c_k)+\lambda} {N+K\lambda} Pλ?(Y=ck?)=N+Kλ∑i=1N?I(yi?=ck?)+λ?
P λ ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) + λ ∑ i = 1 N I ( y i = c k ) + S j λ P_\lambda(X^{(j)}=a_{jl}|Y=c_k)= \frac{\sum_{i=1}^NI(x_i^{(j)}=a_{jl},y_i=c_k)+\lambda} {\sum_{i=1}^NI(y_i=c_k)+S_j\lambda} Pλ?(X(j)=ajl?∣Y=ck?)=∑i=1N?I(yi?=ck?)+Sj?λ∑i=1N?I(xi(j)?=ajl?,yi?=ck?)+λ?
机器学习西瓜书上要求给出测1数据的结果是好瓜还是坏瓜,我们来看测1数据:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 测1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.697 | 0.460 | ? |
在实际代码编写过程中,我们不可能用青绿、蜷缩这些词,所以,我首先对每个变量重复出现做了计数,并把每一个变量的类别进行标号:
x1色泽 0:青绿,1:乌黑,2:浅白
x2根蒂 0:蜷缩,1:稍蜷,2:硬挺
x3敲声 0:浊响,1:沉闷,2:清脆
x4纹理 0:清晰,1:稍糊,2:模糊
x5脐部 0:凹陷,1:稍凹,2:平坦
x6触感 0:硬滑,1:软粘
所以,测1数据等价于:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 测1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.697 | 0.460 | ? |
对于变量x7和x8,我们可以考虑正态分布的概率密度函数,对条件概率:
P
密
度
:
x
7
∣
是
=
p
(
密
度
=
x
7
∣
好
瓜
=
0
)
=
1
2
π
σ
c
,
j
e
x
p
(
?
(
x
i
?
μ
c
,
j
)
2
2
σ
c
,
j
2
)
\\P_{密度:x7|是} =p(密度=x7|好瓜=0)= \frac{1} {\sqrt{2\pi}\sigma_{c,j}}exp(-\frac{(x_i-\mu_{c,j})^2} {2\sigma_{c,j}^2})
P密度:x7∣是?=p(密度=x7∣好瓜=0)=2π?σc,j?1?exp(?2σc,j2?(xi??μc,j?)2?)
P 含 糖 率 = x 8 ∣ 是 = p ( 含 糖 率 = x 8 ∣ 好 瓜 = 0 ) = 1 2 π σ c , j e x p ( ? ( x i ? μ c , j ) 2 2 σ c , j 2 ) \\P_{含糖率=x8|是} =p(含糖率=x8|好瓜=0)= \frac{1} {\sqrt{2\pi}\sigma_{c,j}}exp(-\frac{(x_i-\mu_{c,j})^2} {2\sigma_{c,j}^2}) P含糖率=x8∣是?=p(含糖率=x8∣好瓜=0)=2π?σc,j?1?exp(?2σc,j2?(xi??μc,j?)2?)
P 密 度 : x 7 ∣ 是 = p ( 密 度 = x 7 ∣ 好 瓜 = 1 ) = 1 2 π σ c , j e x p ( ? ( x i ? μ c , j ) 2 2 σ c , j 2 ) \\P_{密度:x7|是} =p(密度=x7|好瓜=1)= \frac{1} {\sqrt{2\pi}\sigma_{c,j}}exp(-\frac{(x_i-\mu_{c,j})^2} {2\sigma_{c,j}^2}) P密度:x7∣是?=p(密度=x7∣好瓜=1)=2π?σc,j?1?exp(?2σc,j2?(xi??μc,j?)2?)
P 含 糖 率 = x 8 ∣ 是 = p ( 含 糖 率 = x 8 ∣ 好 瓜 = 1 ) = 1 2 π σ c , j e x p ( ? ( x i ? μ c , j ) 2 2 σ c , j 2 ) \\P_{含糖率=x8|是} =p(含糖率=x8|好瓜=1)= \frac{1} {\sqrt{2\pi}\sigma_{c,j}}exp(-\frac{(x_i-\mu_{c,j})^2} {2\sigma_{c,j}^2}) P含糖率=x8∣是?=p(含糖率=x8∣好瓜=1)=2π?σc,j?1?exp(?2σc,j2?(xi??μc,j?)2?)
最后来看看代码:
import pandas as pd
import numpy as np
import math
lemon=pd.read_csv(r'C:\Users\Administrator\Desktop\研究生杂项\机器学习\西瓜.txt')
weidu=[]
shuju=[]
lamda=1
yes=0
for i,j in lemon.items():
weidu.append(i.split(' '))
for k in j:
shuju.append(k.split(' '))
for i in range(len(shuju)):
if shuju[i][8]=='是':
yes+=1
No=17-yes
Pyes=(yes+lamda)/(len(shuju)+2*lamda)
Pno=1-Pyes
def condi_p(shuju):
X=[]
sj=[]
for j in range(len(shuju[0])):
for i in range(len(shuju)):
X.append(shuju[i][j])
for k in range(len(shuju[0])):
sj.append(X[(17*k):17*(k+1)])
return sj
def change(list):
re=[]
for i in list:
if list.count(i)>1:
if i not in re:
re.append(i)
for k in range(len(list)):
for j in range(len(re)):
if list[k]==re[j]:
list[k]=j
return list
x1=change(condi_p(shuju)[0])
x2=change(condi_p(shuju)[1])
x3=change(condi_p(shuju)[2])
x4=change(condi_p(shuju)[3])
x5=change(condi_p(shuju)[4])
x6=change(condi_p(shuju)[5])
y=change(condi_p(shuju)[8])
###注意,这里好瓜记为0,坏瓜记为1
##x1色泽 0:青绿,1:乌黑,2:浅白
p10=[]
p11=[]
cnt_1=0
for j in range(3):
for i in range(len(y)):
if (x1[i]==j) and (y[i]==0):
cnt_1+=1
p10.append(cnt_1)
cnt_1=0
for j in range(3):
for i in range(len(y)):
if (x1[i]==j) and (y[i]==1):
cnt_1+=1
p11.append(cnt_1)
cnt_1=0
##x2根蒂 0:蜷缩,1:稍蜷,2:硬挺
p20=[]
p21=[]
cnt_2=0
for j in range(3):
for i in range(len(y)):
if (x2[i]==j) and (y[i]==0):
cnt_2+=1
p20.append(cnt_2)
cnt_2=0
for j in range(3):
for i in range(len(y)):
if (x2[i]==j) and (y[i]==1):
cnt_2+=1
p21.append(cnt_2)
cnt_2=0
##x3 敲声 0:浊响,1:沉闷,2:清脆
p30=[]
p31=[]
cnt_3=0
for j in range(3):
for i in range(len(y)):
if (x3[i]==j) and (y[i]==0):
cnt_3+=1
p30.append(cnt_3)
cnt_3=0
for j in range(3):
for i in range(len(y)):
if (x3[i]==j) and (y[i]==1):
cnt_3+=1
p31.append(cnt_3)
cnt_3=0
##x4 纹理 0:清晰,1:稍糊,2:模糊
p40=[]
p41=[]
cnt_4=0
for j in range(3):
for i in range(len(y)):
if (x4[i]==j) and (y[i]==0):
cnt_4+=1
p40.append(cnt_4)
cnt_4=0
for j in range(3):
for i in range(len(y)):
if (x4[i]==j) and (y[i]==1):
cnt_4+=1
p41.append(cnt_4)
cnt_4=0
##x5 脐部 0:凹陷,1:稍凹,2:平坦
p50=[]
p51=[]
cnt_5=0
for j in range(3):
for i in range(len(y)):
if (x5[i]==j) and (y[i]==0):
cnt_5+=1
p50.append(cnt_5)
cnt_5=0
for j in range(3):
for i in range(len(y)):
if (x5[i]==j) and (y[i]==1):
cnt_5+=1
p51.append(cnt_5)
cnt_5=0
##x6 触感 0:硬滑,1:软粘
p60=[]
p61=[]
cnt_6=0
for j in range(2):
for i in range(len(y)):
if (x6[i]==j) and (y[i]==0):
cnt_6+=1
p60.append(cnt_6)
cnt_6=0
for j in range(2):
for i in range(len(y)):
if (x6[i]==j) and (y[i]==1):
cnt_6+=1
p61.append(cnt_6)
cnt_6=0
##计算拉普拉斯平滑后的条件概率
##色泽
p1_0=[]
p1_1=[]
for i in range(len(p10)):
p1_0.append((p10[i]+lamda)/(yes+len(p10)*lamda))
# print(p1_0)
for i in range(len(p11)):
p1_1.append((p11[i]+lamda)/(No+len(p11)*lamda))
# print(p1_1)
##根蒂
p2_0=[]
p2_1=[]
for i in range(len(p20)):
p2_0.append((p20[i]+lamda)/(yes+len(p20)*lamda))
# print(p1_0)
for i in range(len(p21)):
p2_1.append((p21[i]+lamda)/(No+len(p21)*lamda))
# print(p1_1)
##敲声
p3_0=[]
p3_1=[]
for i in range(len(p30)):
p3_0.append((p30[i]+lamda)/(yes+len(p30)*lamda))
# print(p1_0)
for i in range(len(p31)):
p3_1.append((p31[i]+lamda)/(No+len(p31)*lamda))
# print(p1_1)
##纹理
p4_0=[]
p4_1=[]
for i in range(len(p40)):
p4_0.append((p40[i]+lamda)/(yes+len(p40)*lamda))
# print(p1_0)
for i in range(len(p41)):
p4_1.append((p41[i]+lamda)/(No+len(p41)*lamda))
# print(p1_1)
##脐部
p5_0=[]
p5_1=[]
for i in range(len(p50)):
p5_0.append((p50[i]+lamda)/(yes+len(p50)*lamda))
# print(p1_0)
for i in range(len(p51)):
p5_1.append((p51[i]+lamda)/(No+len(p51)*lamda))
# print(p1_1)
##触感
p6_0=[]
p6_1=[]
for i in range(len(p60)):
p6_0.append((p60[i]+lamda)/(yes+len(p60)*lamda))
# print(p1_0)
for i in range(len(p61)):
p6_1.append((p61[i]+lamda)/(No+len(p61)*lamda))
# print(p1_1)
##处理数值型数据
x7=np.array([float(x) for x in condi_p(shuju)[6]])
x7_0=x7[:8]
x7_1=x7[8:]
x8=np.array([float(x) for x in condi_p(shuju)[7]])
x8_0=x8[:8]
x8_1=x8[8:]
def P_dens_sugar(i,j):
global x7_0,x7_1,x8_0,x8_1
pi0=1/(math.sqrt(2*np.pi)*np.var(x7_0)**0.5)*math.exp(-(i-np.mean(x7_0))**2/(2*np.var(x7_0)))
pi1=1/(math.sqrt(2*np.pi)*np.var(x7_1)**0.5)*math.exp(-(i-np.mean(x7_1))**2/(2*np.var(x7_1)))
pj0=1/(math.sqrt(2*np.pi)*np.var(x8_0)**0.5)*math.exp(-(j-np.mean(x8_0))**2/(2*np.var(x8_0)))
pj1=1/(math.sqrt(2*np.pi)*np.var(x8_1)**0.5)*math.exp(-(j-np.mean(x8_1))**2/(2*np.var(x8_1)))
return pi0,pi1,pj0,pj1
##判断是否为好瓜
test1=[0,0,0,0,0,0,0.697,0.460]
p_good=p1_0[test1[0]]*p2_0[test1[1]]*p3_0[test1[2]]*p4_0[test1[3]]*p5_0[test1[4]]*p6_0[test1[5]]*P_dens_sugar(test1[6],test1[7])[0]*P_dens_sugar(test1[6],test1[7])[2]
p_bad=p1_1[test1[0]]*p2_1[test1[1]]*p3_1[test1[2]]*p4_1[test1[3]]*p5_1[test1[4]]*p6_1[test1[5]]*P_dens_sugar(test1[6],test1[7])[1]*P_dens_sugar(test1[6],test1[7])[3]
if p_good>p_bad:
print('将测1判断为好瓜')
else:
print('将测1判断为坏瓜')
print(p_good,p_bad)
代码运行结果:
