论文:用一阶攻击方法重新思考对抗鲁棒性的经验评估
论文地址:https://arxiv.org/pdf/2006.01304.pdf
有界一阶攻击方法:如快速梯度符号法&投影梯度下降法
论文中作者发现三种情况会导致有界一阶攻击方法使得对抗精度估计过高,而有界一阶攻击方法可以提高鲁棒性。对于每种情况,可以采取解决梯度计算不准确的原因比如数值计算不准确和不可微性,或者通过近似二阶信息迭代攻击的反向传播总数来改善这些三种情况。将补偿策略和攻击方法相结合可以得到更加准确的经验评估指标,通过对模型容量和正则化技术做实验来判断这三种情况的影响,最后发现,即使是传统训练的深度神经网络,也普遍存在不表示鲁棒性的高估对抗准确性,并强调了在没有保证界限的情况下使用经验评估的注意事项。
1.Introduction
对抗性样本的鲁棒性成为了设计深层神经网络的一个重要因素,使得人们更多的投入对基准体系结构和正则化技术鲁棒性的研究。理解对抗性攻击鲁棒性的一个重要而且具有挑战的方法是精准评估对抗性实验的鲁棒性。
对于一个样本x在经过Lp范数后其数值在一个球的范围内,对抗性样本的鲁棒性在于r的存在。深度神经网络对x和x+r的预测是不一样的,在高维度上很难解释。总的来说,目前使用有界一阶攻击方法生成的r对预测进行经验测试成为一种流行的方法,这两种算法(快速梯度符号法&投影梯度下降法)能够有效地生成r,且反向传播很少。但是这些方法只是生成了鲁棒性的上界,攻击方法无法找到对抗性示例可能并不意味着真正的健壮性。
为了获得更加精确的对抗鲁棒性经验指标,了解攻击方法的失败何时不代表鲁棒性是很重要的,像梯度遮掩是使攻击方法使用的梯度不准确而削弱了对抗准确性。
在这些情况下有界一阶攻击方法失败找不到对抗性示例不算失败
我们确定了三种因为某些原因导致的有界一阶攻击方法不成功的情况(也普遍存在于各种传统训练的深度神经网络中,跨越不同的体系结构和数据集,而不仅仅局限于专门设计用于造成梯度掩蔽的特定防御):
- 交叉熵损失接近于零,导致梯度计算不准确
- 不可微的激活、池化引起梯度消失
- 某些训练条件导致深层神经网络不太适合一阶近似,从而增加迭代攻击的迭代次数
2.符号和定义
贯穿全文的符号
x: clearn的输入
f(·): 神经网络
z = f(x): 输出
y =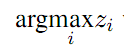
导数: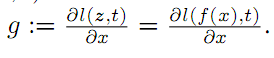
加了轻微扰动如果函数值还是等于自身说明鲁棒性很好
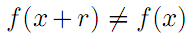
2.1实验用的数据介绍
2.2实验用的网络架构介绍
2.3对抗性攻击方法
有界一阶攻击方法通常用来研究L1、L2正则的对抗性稳健性,对于未标记的对抗性样本主要用于白盒测试。
2.4用的框架
3.分析三种导致的有界一阶攻击方法不成功原因并提出改进策略
3.1zero loss
loss=0出现梯度消失导致反向传播不提供任何信息;loss--->0也会出现zero loss的情况

在CIFAR-10上未经显式正则化训练的简单模型的实验中,我们还观察到梯度掩蔽的症状,特别是黑盒攻击比白盒攻击更强,意味着模型的对抗准确度可能被高估。但我们也发现许多攻击(如FGSM)失败的样本(接近)零损失(<10。
解决措施:确保损耗值足够大,以便能够准确计算梯度。
- 通过缩放,f(x)除以一个常数T>1,可以得到较大的交叉熵损失。
- 改变t(从ground_truth的label换成别的类别标签)交叉熵损失也增加。
对比上面两钟办法发现,后一种方法会使得白盒攻击更有效,使得FGSM攻击方法的成功率高达11%,PGD攻击方法的成功率高达4.5%。但观察表一发现由zero loss引起梯度掩盖现象可能普遍存在。
3.2不可微性(不可微的激活、池化引起)

因为函数的不可微性导致的梯度破碎是一种梯度掩蔽。作者分析了ReLU和最大池引起的固有不可微性如何微妙地影响攻击方法,以及如何改进并使用后向传播攻击。
- ReLU操作原本<0的部分在受到r干扰之后会大于0,这时候梯度不再继续,因为最终预测的有效神经元发生了变化。
- 当扰动改变每个池窗口的最大神经元时,最大池化也存在类似问题。
解决办法:用类似但可微的函数替换不可微函数
利用BPDA在其不可微点周围平滑地近似ReLU和max池的行为,用softplus替换ReLU,用Lp norm pooling替换max pooling,用P5替换Lp norm pooling,可以作为BPDA的默认设置,特别是在补偿此现象和零损失现象时。
不可微性通常会产生细微的差异(1%),尤其是对于R-FGSM和PGD。尽管如此,仍有一些模型受到不可微性的显著影响,例如在SVHN上训练的aWRN 28,其显示FGSM的差异超过10%。此外,FGSM似乎比其他攻击方法受到的影响更大,这可以通过R-FGSM和PGD的有效步长较小来解释,因为较小的步长会导致神经元切换频率较低。例如,PGD对每次迭代使用小步距,而R-FGSM通常采用2步距,而不是由于增加了随机扰动。我们还报告了当攻击同时补偿了零损失和不可微性时的对抗准确性。
3.3某些训练条件导致深层神经网络不太适合一阶近似,从而增加迭代攻击的迭代次数

解决方法:加入二阶信息以减少反向传播的总数
对在CIFAR-10上训练的aWRN 28过度应用重量衰减(随着训练的进行,重量衰减的强度不断增加)可以通过少量迭代提高对抗PGD的对抗精度,补偿了零损失和不可微性,但与没有针对大量迭代进行显式正则化的模型相比,最终并没有表现出明显的优势,但简单地过度应用权重衰减可以提供优势。
大量迭代是防止高估对抗精度的简单方法。当攻击方法具有随机性时使用多个随机启动的众所周知的原因:PGD的随机初始化会影响后续一阶迭代的成功,并且成功初始化(一阶迭代从中发现对抗性示例)每次迭代会导致更大的损失增加和梯度大小(L2范数)。尽管观察结果本身可能微不足道,但它们暗示,初始化到梯度变化迅速的点(因此具有高曲率),可能有助于后续一阶迭代轻松找到对立的示例。
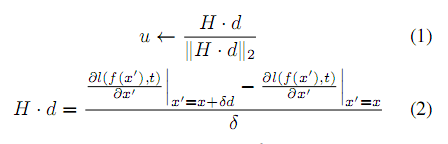
d: 从N(0;I)中随机采样,并归一化为单位向量
该方法使用两个额外的反向传播来计算u,我们使用u作为PGD(PGD特征值)的
初始化方向,而不是随机向量

4.通过对模型容量和正则化技术的案例研究来证明三种现象的影响
4.1模型容量
4.1.1模型容量

通过对比不同深度的相同网络结构,发现宽度较大的模型确实显示出更好的对抗准确性,但它们相对于较小模型的优势可能被夸大了;深度为1和16的对抗精度差为10.14%,但补偿零损失和不可微性只会导致0.41%的差异。宽度较大的模型的对抗精度往往被高估,尤其是由于零损失现象。
4.1.2权重修剪
我们可以通过利用补偿策略,找到是哪些问题导致出现这三种现象的原因,以防止产
生误导性结论。

我们迭代删减大型WRN 28的权重,以及微调,包括固定权重衰减和不固定权重衰减,并测量对抗精度。在训练和微调过程中没有重量衰减,随着更多重量被削减,对抗基线攻击的准确度显著下降。
然而,应用补偿方法表明,对抗性准确度实际上下降不到1%,与清洁准确度类似。差异的主要来源是零损失现象,因为原始密集模型的对抗精度因该现象而被高估,而修剪过的 稀疏模型实际上对该现象的依赖程度较低。
一方面,通过迭代剪枝和权重衰减,对抗基线攻击的准确度增加了3.5%,但补偿后的准确度增加不到0.4%。而且微调时使用权重衰减会增加大量的时间段,作用类似于3.3节中说得过度权重衰减
4.2正则化技术
