高斯分布

正态分布公式
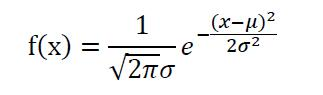
在这里插入图片描述
正态分布函数密度曲线可以表示为：称x服从正态分布，记为X~N(μ,σ2)，
其中μ为均数，σ为标准差。μ决定了正态分布的位置，与μ越近，被取到的概率就越大，反之越小。σ描述的是正态分布的离散程度。σ越大，数据分布越分散曲线越扁平；σ越小，数据分布越集中曲线越陡峭。X∈（-∞，+ ∞ )。标准正态分布另正态分布的μ为0，σ为1。
高斯函数

import numpy as np
import matplotlib.pyplot as plt
import math

x = np.arange(-10, 10, 0.1)
mu= 0
sigma = 1
y = 1/(math.sqrt(2 * np.pi) * sigma) * np.exp(-((x - mu) ** 2)/(2 * sigma**2))
plt.plot(x, y, 'r')
plt.show()

在这里插入图片描述

3D高斯函数

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x,y = np.mgrid[-10:10:200j,-10:10:200j]
sigma = 3
z = 1/(2 * np.pi * (sigma**2)) * np.exp(-(x**2+y**2)/(2 * sigma**2))

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow',alpha = 0.9)

plt.show()

在这里插入图片描述

高斯拟合

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy import stats

# yourlist = [0,1,2,3,4,1,3,4,3,5,4,3,2,1]
# x = np.array(yourlist)
x=pd.DataFrame(np.random.randn(100)+10,columns = ['value'])

mu = np.mean(x)  # 计算均值
sigma = np.std(x)
num_bins = 30  # 直方图柱子的数量
n, bins, patches = plt.hist(x, num_bins, density=1, alpha=0.75)
# 直方图函数，x为x轴的值，normed=1表示为概率密度，即和为一，绿色方块，色深参数0.5.返回n个概率，直方块左边线的x值，及各个方块对象
y = stats.norm.pdf(bins, mu, sigma)  # 拟合一条最佳正态分布曲线y

# plt.grid(True)
plt.plot(bins, y, 'r--')  # 绘制y的曲线
plt.show()

在这里插入图片描述

高斯判断

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy import stats

# yourlist = [0,1,2,3,4,1,3,4,3,5,4,3,2,1]
# x = np.array(yourlist)
x= pd.DataFrame(np.random.randn(100)+10, columns =['value'])

mu = np.mean(x)  # 计算均值
sigma = np.std(x) # 计算标准差
num_bins = 30  # 直方图柱子的数量
n, bins, patches = plt.hist(x, num_bins, density=1, alpha=0.75)
# 直方图函数，x为x轴的值，normed=1表示为概率密度，即和为一，绿色方块，色深参数0.5.返回n个概率，直方块左边线的x值，及各个方块对象
y = stats.norm.pdf(bins, mu, sigma)  # 拟合一条最佳正态分布曲线y

plt.grid(True)
plt.plot(bins, y, 'r--')  # 绘制y的曲线
print(stats.kstest(x['value'], 'norm', (mu, sigma))[1])
if(stats.kstest(x['value'], 'norm', (mu, sigma))[1]> 0.05):
    plt.title('Normal distribution')
plt.show()