[人工智能]机器学习——树回归

CART算法

什么是CART？

CART是英文Classification And Regression Tree的简写，又称为分类回归树。从它的名字我们就可
以看出，它是一个很强大的算法，既可以用于分类还可以用于回归，所以非常值得我们来学习。

CART算法使用的就是二元切分法，这种方法可以通过调整树的构建过程，使其能够处理连续型变量。

具体的处理方法是：如果特征值大于给定值就走左子树，否则就走右子树。

CART算法有两步：

1. 决策树生成：递归地构建二叉决策树的过程，基于训练数据集生成决策树，生成的决策树要尽量大；自上而下从根开始建立节点，在每个节点处要选择一个最好的属性来分裂，使得子节点中的训 练集尽量的纯。
2. 决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这时损失函数最小作为剪枝的 标准。

CART树的构建过程：

首先找到最佳的列来切分数据集，每次都执行二元切分法，如果特征值大于给定值就走左子树，否则就走右子树，当节点不能再分时就将该节点保存为叶节点。

这里我们介绍回归树和模型树。

区别：

回归树：叶子结点为特征值的平均值。
模型树：叶子结点为线性方程。

一：回归树

自定义回归树的数据为整条数据，即特征列后面紧跟目标列。
主要函数：

binSplitDataSet(dataSet, feature, value)#根据特征切分数据集合 
errType(dataSet)#计算总方差：均方差*样本数
leafType(dataSet)#生成叶节点
chooseBestSplit(dataSet, leafType=leafType, errType=errType, ops = (1,4))#找到数据的最佳二元切分方式函数
createTree(dataSet, leafType = leafType, errType = errType, ops = (1, 4))#树构建函数 

手动实现回归树code：

""" 
函数说明:根据特征切分数据集合 
参数说明: 
	dataSet：原始数据集 
	feature：待切分的特征索引 
	value：该特征的值 
返回:
	mat0：切分的数据集合0 
	mat1：切分的数据集合1 
"""
def binSplitDataSet(dataSet, feature, value):
    mat0 = dataSet.loc[dataSet.iloc[:,feature] > value,:]
    mat0.index = range(mat0.shape[0])
    mat1 = dataSet.loc[dataSet.iloc[:,feature] <= value,:]
    mat1.index = range(mat1.shape[0])
    return mat0, mat1

#计算总方差：均方差*样本数
def errType(dataSet):
    var= dataSet.iloc[:,-1].var() *dataSet.shape[0]
    return var

#生成叶节点
def leafType(dataSet):
    leaf = dataSet.iloc[:,-1].mean()
    return leaf

""" 
    函数说明:找到数据的最佳二元切分方式函数 
    参数说明: 
        dataSet：原始数据集 
        leafType：生成叶结点函数 
        errType：误差估计函数 
        ops：用户定义的参数构成的元组 
    返回:
        bestIndex：最佳切分特征 
        bestValue：最佳特征值 
"""
def chooseBestSplit(dataSet, leafType=leafType, errType=errType, ops = (1,4)):
    #tolS允许的误差下降值,tolN切分的最少样本数
    tolS = ops[0]; tolN = ops[1]
    #如果当前所有值相等,则退出。(根据set的特性)
    if len(set(dataSet.iloc[:,-1].values)) == 1:
        return None, leafType(dataSet)
    #统计数据集合的行m和列n
    m, n = dataSet.shape
    #默认最后一个特征为最佳切分特征,计算其误差估计
    S = errType(dataSet)
    #分别为最佳误差,最佳特征切分的索引值,最佳特征值
    bestS = np.inf; bestIndex = 0; bestValue = 0
    #遍历所有特征列
    for featIndex in range(n - 1):  #原始数据集是带标签的，特征个数就是n-1
        colval= set(dataSet.iloc[:,featIndex].values) #提取出当前切分列的所有取值
        #遍历所有特征值
        for splitVal in colval:
            #根据特征和特征值切分数据集
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            #如果数据少于tolN,则退出
            if (mat0.shape[0] < tolN) or (mat1.shape[0] < tolN): continue
            #计算误差估计
            newS = errType(mat0) + errType(mat1)
            #如果误差估计更小,则更新特征索引值和特征值
            if newS < bestS:
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    #如果误差减少不大则退出
    if (S - bestS) < tolS:
        return None, leafType(dataSet)
    #根据最佳的切分特征和特征值切分数据集合
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    #如果切分出的数据集很小则退出
    if (mat0.shape[0] < tolN) or (mat1.shape[0] < tolN):
        return None, leafType(dataSet)
    #返回最佳切分特征和特征值
    return bestIndex, bestValue

""" 
    函数功能:树构建函数 
    参数说明: 
        dataSet：原始数据集 
        leafType：建立叶结点的函数 
        errType：误差计算函数 
        ops：包含树构建所有其他参数的元组 
    返回:
        retTree：构建的回归树 
"""
def createTree(dataSet, leafType = leafType, errType = errType, ops = (1, 4)):
    #选择最佳切分特征和特征值
    col, value = chooseBestSplit(dataSet, leafType, errType, ops)
    #如果没有特征,则返回特征值
    if col == None: return value
    #回归树
    retTree = {}  #储存树的信息
    retTree['spInd'] = col
    retTree['spVal'] = value
    #分成左数据集和右数据集
    lSet, rSet = binSplitDataSet(dataSet, col, value)
    #创建左子树和右子树
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree  

回归树的SKlearn实现：

数据集：

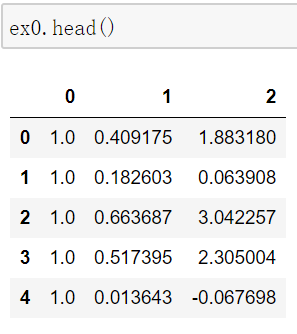
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model

#用来训练的数据
x = (ex0.iloc[:,1].values).reshape(-1,1)
y = (ex0.iloc[:,-1].values).reshape(-1,1)

# 训练模型
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = linear_model.LinearRegression()
model1.fit(x, y)
model2.fit(x, y)
model3.fit(x, y)

# 预测
X_test = np.arange(0, 1, 0.01).reshape(-1,1)
y_1 = model1.predict(X_test)
y_2 = model2.predict(X_test)
y_3 = model3.predict(X_test)

# 可视化结果
plt.figure() #创建画布
plt.scatter(x, y, s=20, edgecolor="black",c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",label="max_depth=1", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=3", linewidth=2)
plt.plot(X_test, y_3, color='red', label='liner regression', linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

效果：

二：模型树

用树来对数据进行建模，除了把叶节点简单地设定成常数值之外，还有一种方法是把叶节点设定为分段线性函数，这里的分段线性函数（piecewise linear）指的是模型由多个线性片段组成。

在前面讲的回归树中，每个叶节点中包含的是单个值；下面我们要讲的这种模型树，每个叶节点中包含的就是一个线性方程。

手动实现模型树code：

""" 函数功能：测试输入变量是否是字典类型，返回布尔类型的结果 """
def isTree(obj):
    return type(obj).__name__=='dict'

""" 
    函数功能：计算特征矩阵、标签矩阵、回归系数 
    参数说明： 
        dataSet：原始数据集 
    返回：
        ws：回归系数 
        X：特征矩阵（第一列增加x0=1） 
        Y：标签矩阵 
"""
def linearSolve(dataSet):
    m,n = dataSet.shape
    con = pd.DataFrame(np.ones((m,1)))#在第一列增加一列常数值X0=1
    conX = pd.concat([con,dataSet.iloc[:,:-1]],axis=1,ignore_index=True)
    X = np.mat(conX)
    Y = np.mat(dataSet.iloc[:,-1].values).T
    xTx = X.T*X
    if np.linalg.det(xTx) == 0:
        raise NameError('奇异矩阵无法求逆，请尝试增大tolN,即ops第二个值')
    ws = xTx.I*(X.T*Y)
    return ws,X,Y

"""生成模型树的叶节点（即线性方程），这里返回的是回归系数"""
def modelLeaf(dataSet):
    ws,X,Y = linearSolve(dataSet)
    return ws

"""计算给定数据集的误差（误差平方和）"""
def modelErr(dataSet):
    ws,X,Y = linearSolve(dataSet)
    yHat = X*ws
    err = sum(np.power(Y-yHat,2))
    return err

#利用回归树的createTree函数构建模型树
createTree(exp2,modelLeaf,modelErr,(1, 10))

三：构建预测函数的辅助函数

回归树和模型树的预测函数：

#回归树叶节点预测函数
def regTreeEval(model,inData):
    return model

#模型树叶节点预测函数
def modelTreeEval(model,inData):
    n = len(inData)
    X = np.mat(np.ones((1,n+1)))  #增加一列常数项x0=1,放在第一列
    X[:,1:n+1] = inData
    return X*model

预测结果：

"""
    函数功能：返回单个测试数据的预测结果 
    参数说明： 
        tree：字典形式的树 
        inData：单条测试数据 
        modelEval：叶节点预测函数
"""
def treeForeCast(tree,inData,modelEval = regTreeEval):
    #先判断是不是叶节点，如果是叶节点直接返回预测结果
    if not isTree(tree):
        return modelEval(tree,inData)
    #根据索引找到左右子树
    if inData[tree['spInd']] > tree['spVal']: 
        #如果左子树不是叶节点，则递归找到叶节点
        if isTree(tree['left']):
            return treeForeCast(tree['left'],inData,modelEval)
        else:
            return modelEval(tree['left'],inData)
    else:
        if isTree(tree['right']):
            return treeForeCast(tree['right'],inData,modelEval)
        else:
            return modelEval(tree['right'],inData)

""" 
    函数功能：返回整个测试集的预测结果 
    参数说明： 
        tree:字典形式的树 
        testData:测试集 
        modelEval：叶节点预测函数 
    返回：
        yHat:每条数据的预测结果 
"""
def createForeCast(tree, testData, modelEval = regTreeEval):
    m = testData.shape[0]
    yHat = np.mat(np.zeros((m,1)))
    for i in range(m):
        inData = testData.iloc[i,:-1].values
        yHat[i,0]= treeForeCast(tree,inData,modelEval)
    return yHat

回归树的预测代码：

#创建回归树
regTree = createTree(biketrain,ops=(1,20))
#回归树预测结果
yHat = createForeCast(regTree,biketest, regTreeEval)
#计算相关系数R2
np.corrcoef(yHat.T,biketest.iloc[:,-1].values)[0,1]
#计算均方误差SSE
sum((yHat.A.flatten()-biketest.iloc[:,-1].values)**2)

模型树的预测代码：

#创建模型树
modelTree = createTree(biketrain, modelLeaf, modelErr, ops=(1,20))
#模型树预测结果
yHat1 = createForeCast( modelTree, biketest, modelTreeEval)
#计算相关系数R2
np.corrcoef(yHat1.T,biketest.iloc[:,-1].values)[0,1]
#计算均方误差SSE
sum((yHat1.A.flatten()-biketest.iloc[:,-1].values)**2)

标准线性回归：

#标准线性回归
ws,X,Y = linearSolve(biketrain)
#在第一列增加常数项1,构建特征矩阵
testX = pd.concat([pd.DataFrame(np.ones((biketest.shape[0],1))),biketest.iloc[:,:-1]],
                  axis=1,ignore_index = True)
testMat = np.mat(testX)
#标准线性回归预测结果
yHat_2 = testMat*ws
#相关系数R2
R2_2 = np.corrcoef(yHat_2.T,biketest.iloc[:,-1].values)[0,1]
#均方误差SSE
SSE_2 = sum((yHat_2.A.flatten()-biketest.iloc[:,-1].values)**2)