结论

过滤法更快速，但更粗糙。包装法和嵌入法更精确，比较适合具体到算法去调整，但计算量比较大，运行时间长。当数据量很大的时候，优先使用方差过滤和互信息法调整，再上其他特征选择方法。使用逻辑回归时，优先使用嵌入法。使用支持向量机时，优先使用递归消除特征。

1、读数据，定义测试函数

import pandas as pd
data = pd.read_csv(r'F:\教师培训\ppd7\df_Master_merge_clean.csv',encoding='gb18030')
pd_x = data[data.target.notnull()].drop(columns=['Idx', 'target', 'sample_status', 'ListingInfo'])
pd_y = data[data.target.notnull()]['target']

#定义画图auc函数
def get_auc(x, y):
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import roc_auc_score, roc_curve
    import lightgbm as lgb
    
    #画出auc图的函数     
    def roc_auc_plot(clf,x_train,y_train,x_test, y_test):
        train_auc = roc_auc_score(y_train,clf.predict_proba(x_train)[:,1])
        train_fpr, train_tpr, _ = roc_curve(y_train,clf.predict_proba(x_train)[:,1])
        train_ks = abs(train_fpr-train_tpr).max()
        print('train_ks = ', train_ks)
        print('train_auc = ', train_auc)

        test_auc = roc_auc_score(y_test,clf.predict_proba(x_test)[:,1])
        test_fpr, test_tpr, _ = roc_curve(y_test,clf.predict_proba(x_test)[:,1])
        test_ks = abs(test_fpr-test_tpr).max()
        print('test_ks = ', test_ks)
        print('test_auc = ', test_auc)

        from matplotlib import pyplot as plt
        plt.plot(train_fpr,train_tpr,label = 'train_roc')
        plt.plot(test_fpr,test_tpr,label = 'test_roc')
        plt.plot([0,1],[0,1],'k--', c='r')
        plt.xlabel('False positive rate')
        plt.ylabel('True positive rate')
        plt.title('ROC Curve')
        plt.legend(loc = 'best')
        plt.show()

    x_train,x_test, y_train, y_test = train_test_split(x,y,random_state=2,test_size=0.2)

    lgb_model = lgb.LGBMClassifier(n_estimators=800,
                                    boosting_type='gbdt',
                                   learning_rate=0.04,
                                   min_child_samples=68,
                                   min_child_weight=0.01,
                                      max_depth=4,
                                  num_leaves=16,
                                  colsample_bytree=0.8,
                                  subsample=0.8,
                                  reg_alpha=0.7777777777777778,
                                  reg_lambda=0.3,
                                   objective='binary')

    clf = lgb_model.fit(x_train, y_train,
                  eval_set=[(x_train, y_train),(x_test,y_test)],
                  eval_metric='auc',early_stopping_rounds=100)
    roc_auc_plot(clf,x_train,y_train,x_test, y_test)


#定义基分类器
clf1 = lgb.LGBMClassifier(n_estimators=800,
                          boosting_type='gbdt',
                          learning_rate=0.04,
                          min_child_samples=68,
                          min_child_weight=0.01,
                             max_depth=4,
                         num_leaves=16,
                         colsample_bytree=0.8,
                         subsample=0.8,
                         reg_alpha=0.7777777777777778,
                         reg_lambda=0.3,
                          objective='binary')

2、各种方法如下

1.递归消除特征

递归特征消除法（Recursive feature elimination, 简写为RFE），使用很少的特征达到很优秀的效果。
它反复创建模型，并在每次迭代时保留最佳特征或剔除最差特征，下一次迭代时，它会使用上一次建模中没有被选中的特征来构建下一个模型，直到所有特征都耗尽为止。然后，它根据自己保留或
剔除特征的顺序来对特征进行排名，最终选出一个最佳子集。

代码如下（示例）：

from sklearn.feature_selection import RFE

#只有fit,表示这是一个选择器，可以有属性
#n_features_to_select：是想要选择的特征个数
#support_：返回所有的特征的是否最后被选中的布尔矩阵
#ranking_:返回特征的按数次迭代中综合重要性的排名
#step表示每次迭代中希望移除的特征个数
c = RFE(clf1, n_features_to_select=i, step=50).fit(pd_x, pd_y)
c.support_.sum()
c.ranking_

#fit_transform返回筛选后的数据集
c = RFE(clf1, n_features_to_select=i, step=50).fit_transform(pd_x, pd_y)

##########################################################################


#利用交叉验证选择最优的特征个数，运行速度太长了，此结果没有出来，所以无法展示验证
axisx = range(1,250,10)
scores = []
for i in axisx:
    x_wrapper = RFE(clf1, n_features_to_select=i, step=50).fit_transform(pd_x, pd_y)
    score = cross_val_score(clf1,x_wrapper, pd_y, cv=5).mean()
    scores.append(score)

plt.figure(figsize=(20,5))
plt.plot(axisx,scores, label='n_features_to_select-score')
plt.xticks(axisx)
plt.legend()
plt.show()
#如图筛选出最优特征个数113

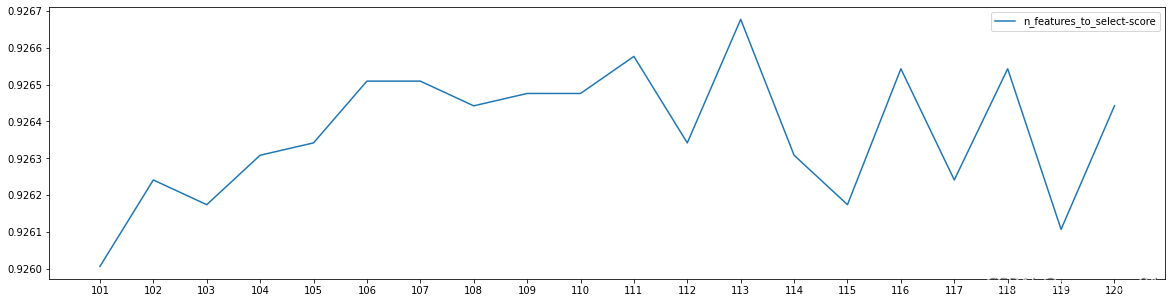
在这里插入图片描述


x_rfe = RFE(clf1, n_features_to_select=113, step=50).fit_transform(pd_x, pd_y)
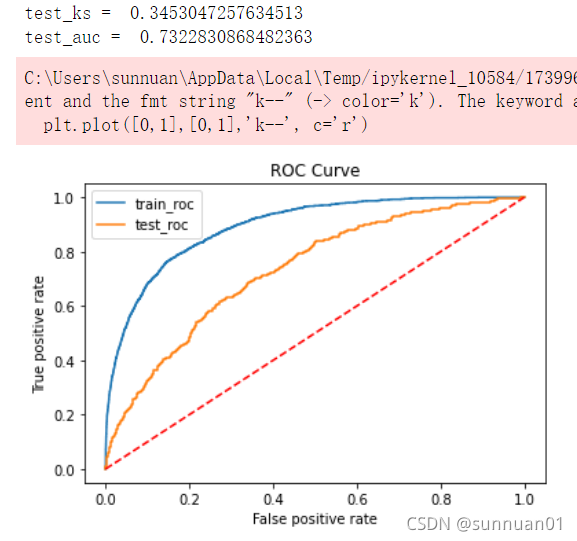
#画出auc曲线
get_auc(x_rfe, pd_y)
#416个特征降到113个特征，效果从test_auc =  0.74109449149997降到0.7322830868482363

在这里插入图片描述

2.Embedded嵌入法

代码如下（示例）：
1.先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据权值系数从大到小选择特征,这些权值系数往往代表了特征对于模型的某种贡献或某种重要性，比如决策树和树的集成模型中的feature_importances_属性，可以列出各个特征对树的建立的贡献，我们就可以基于这种贡献的评估，找出对模型建立最有用的特征。

from sklearn.feature_selection import SelectFromModel
from sklearn.model_selection import cross_val_score 

#estimator：使用的模型评估器，只要是带feature_importances_或者coef_属性，或带有l1和l2惩罚项的模型都可以使用
#threshold：特征重要性的阈值，重要性低于这个阈值的特征都将被删除

# 选取重要性的最大值,目的是为了构造axisx,选择最优的threshold
m = clf1.fit(pd_x, pd_y).feature_importances_.max()
axisx = range(0,m+1,10)

#寻找最优threshold函数
def get_opt_thre(axisx):
    scores = []
    for i in axisx:
        #threshold特征重要性的阈值，重要性低于这个阈值的特征都将被删除
        embedded_x = SelectFromModel(clf1, threshold=i).fit_transform(pd_x, pd_y)
        score = cross_val_score(clf1, embedded_x,pd_y, cv=5).mean()
        scores.append(score)

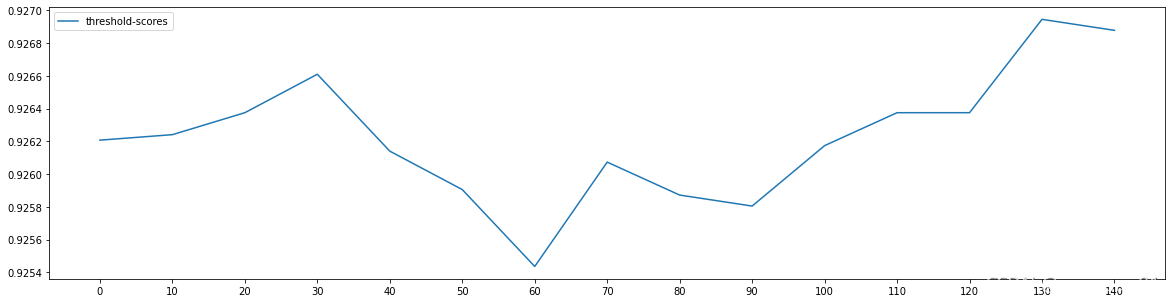
    plt.figure(figsize=(20,5))
    plt.plot(axisx, scores, label='threshold-scores')
    plt.xticks(axisx)
    plt.legend()
    plt.show()
get_opt_thre(axisx)
#观察下图，最优值在130左右，最大的特征重要分数是140，这样选择选到的特征极度少，所以不选取此值，推断可能是评价指标的问题。
选择30

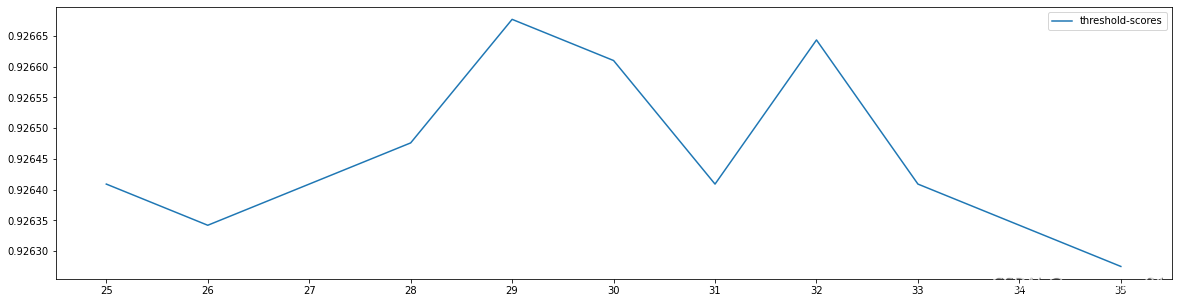
在这里插入图片描述

axisx = range(25,36,1)
get_opt_thre(axisx)
#从图像上来看，随着阈值越来越高，模型的效果逐渐变差，被删除的特征越来越多，信息损失也逐渐变大

embedded_x = SelectFromModel(clf1, threshold=29).fit_transform(pd_x, pd_y)
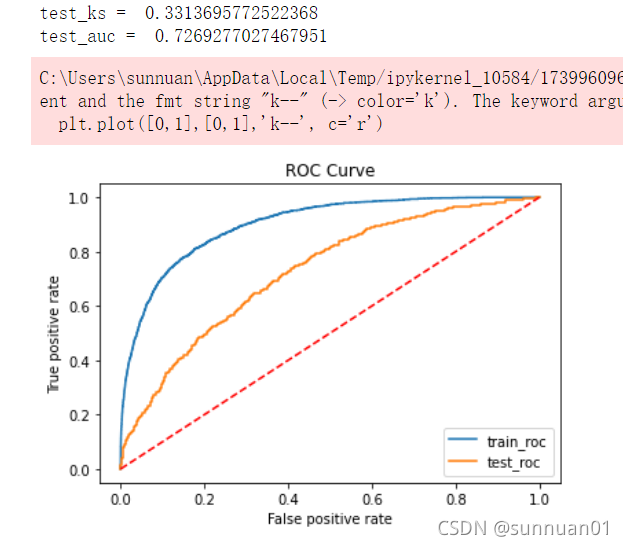
get_auc(embedded_x, pd_y)

#416个特征降到120个特征，效果从test_auc =  0.74109449149997降到0.7269277027467951

在这里插入图片描述

3.相关性过滤之互信息法

互信息法是用来捕捉每个特征与标签之间的任意关系（包括线性和非线性关系）的过滤方法
feature_selection.mutual_info_classif（互信息分类）和feature_selection.mutual_info_regression（互信息回归）。互信息法比F检验更加强大，F检验只能够找出线性关系，而互信息法可以找出任意关系。互信息法不返回p值或F值类似的统计量，它返回“每个特征与目标之间的互信息量的估计”，这个估计量在[0,1]之间取值，为0则表示两个变量独立，为1则表示两个变量完全相关。以互信息分类为例的代码如下：

from sklearn.feature_selection import mutual_info_classif

res = mutual_info_classif(pd_x, pd_y)
mc = pd.DataFrame({'fname':pd_x.columns, 'micv':res})
f = mc[mc.micv>0]['fname']
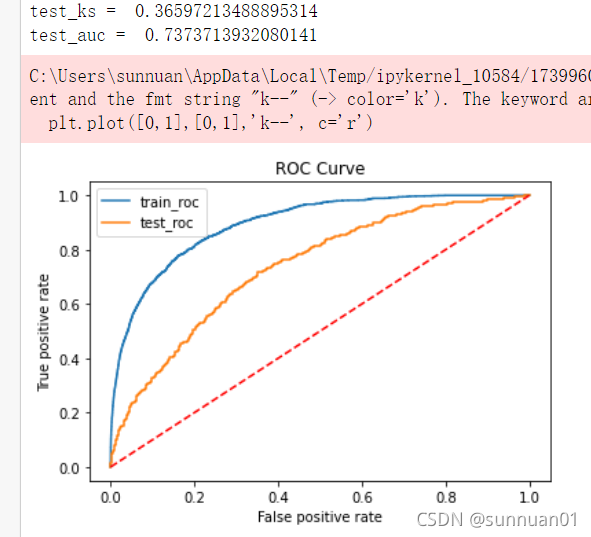
get_auc(pd_x[f], pd_y)
#416个特征降到271个特征，效果从test_auc =  0.74109449149997降到0.7373713932080141

在这里插入图片描述

4.相关性过滤之F检验

# F检验，又称ANOVA，方差齐性检验，是用来捕捉每个特征与标签之间的线性关系的过滤方法,
# F检验分类用于标签是离散型变量的数据，而F检验回归用于标签是连续型变量的数据。
#原假设是”数据不存在显著的线性关系“。它返回F值和p值两个统计量。和卡方过滤一样，我们希望选取p值小于#0.05或0.01的特征，
#这些特征与标签时显著线性相关的，而p值大于0.05或0.01的特征则被我们认为是和标签没有显著线性关系的特征，应该被删除。

from sklearn.feature_selection import f_classif

F, p = f_classif(x,y)
sf = pd.DataFrame({'fname':x.columns, 'p':p})
fname = sf[sf.p<0.05]['fname']
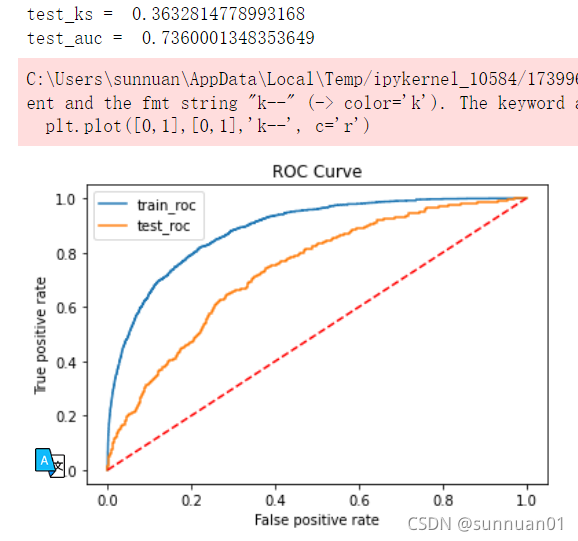
get_auc(x[fname], y)
#416个特征降到201个特征，效果从test_auc =  0.74109449149997降到0.7360001348353649

在这里插入图片描述

5.相关性过滤之F检验

#卡方过滤是专门针对离散型标签（即分类问题）的相关性过滤。卡方检验类feature_selection.chi2计算每个非负特征和标签之间的卡方统计量，并依照卡方统计量由高到低为特征排名。由于数据集中含有负值，故不采用这种方式.

from sklearn.feature_selection import chi2, SelectKBest

#假设在这里我一直我需要300个特征
x_chi = SelectKBest(chi2, k=300).fit_transform(pd_x, y)
et_auc(x_chi, y)

6.方差过滤

通过特征本身的方差来筛选特征的类。比如一个特征本身的方差很小，就表示样本在这个特征上基本没有差异，可能特征中的大多数值都一样，甚至整个特征的取值都相同，那这个特征对于样本区分没有什么作用。所以无论接下来的特征工程要做什么，都要优先消除方差为0的特征。VarianceThreshold有重要参数threshold，表示方差的阈值，表示舍弃所有方差小于threshold的特征，不填默认为0，即删除所有的记录都相同的特征。

from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold() #实例化，不填参数默认方差为0
X_var0 = selector.fit_transform(X) #获取删除不合格特征之后的新特征矩阵
#发现没有方差为0的特征

最近邻算法KNN，单棵决策树，支持向量机SVM，神经网络，回归算法，都需要遍历特征或升维来进
行运算，所以他们本身的运算量就很大，需要的时间就很长，因此方差过滤这样的特征选择对他们来说就尤为重要。
但对于不需要遍历特征的算法，比如随机森林，它随机选取特征进行分枝，本身运算就非常快速，因此特征选择对它来说效果平平。