[人工智能]论文笔记--Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting

Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting (AAAI 19)

Summary

作者提出ASTGCN的主要由三个独立组件组成，分别对交通流的三种节奏特性(近期依赖、日周期依赖和周周期依赖)进行建模。每个组件包含两个主要部分：1)有效捕获交通数据中动态时空相关性的时空注意机制；2)时空卷积，即同时使用图卷积来捕获空间模式和通用标准卷积来捕获时间特征。三个组件的结果相融合得到最终预测结果。

Problem Definition

交通预测问题最大挑战还是如何有效提取数据的时空相关性。如下图

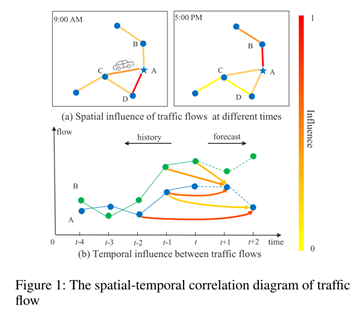
线条颜色越深，影响越大。从图(a)表示的是空间依赖的关系，不同的地点对A的影响是不同的，即使是同一个地点随着时间的推移对A的影响也是不同的。在时间维度下图（b），不同位置的历史观测结果对A未来不同时段的交通状态有不同的影响。综上所述，公路网交通数据相关性在空间维度和时间维度上均表现出较强的动态性。

问题定义

将交通网络定义为一个无向图表示为$G=(V,E,A)$，V表示节点列表，E是边集，$A\in {\mathbb{R}}^{N\times N}$是邻接矩阵。定义$\mathcal{X}={\left({\mathbf{X}}_1,{\mathbf{X}}_2,\dots ,{\mathbf{X}}_{\tau }\right)}^T\in {\mathbb{R}}^{N\times F\times \tau }$表示τ时间内所有节点的所有特征值。利用交通网络中所有节点在过去$\tau$时间内的各种历史测度，预测未来交通流序列$(y^1,y^2,...,y^N{)}^t\in {\mathbb{R}}^{N\times T_p}$。

Method

ASTGCN算法框架

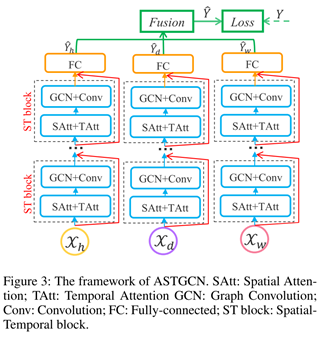
输入

①${\mathcal{X}}_h=\left({\mathbf{X}}_{t_0?T_h+1},{\mathbf{X}}_{t_0?T_h+2},\dots ,{\mathbf{X}}_{t_0}\right)\in {\mathbb{R}}^{N\times F\times T_h}$表示的是最近时间段交通信息，长度为Th。从直观上看，交通拥挤的形成和扩散是渐进的。因此，过去的交通流必然会对未来的交通流产生影响。

②
$$\begin{array}{rl}& {\mathcal{X}}_d=({\mathbf{X}}_{t_0?\left(T_d/T_p\right)?q+1},\dots ,{\mathbf{X}}_{t_0?\left(T_d/T_p\right)?q+T_p}\\ & {\mathbf{X}}_{t_0?\left(T_d/T_p?1\right)?q+1},\dots ,{\mathbf{X}}_{t_0?\left(T_d/T_p?1\right)?q+T_p},?\\ & {\mathbf{X}}_{t_0?q+1},\dots ,{\mathbf{X}}_{t_0?q+T_p})\in {\mathbb{R}}^{N\times F\times T_d}\end{array}$$
表示日周期时间段交通信息，长度为Td。公式中q表示一天采集的时间步长度。由于人的日常规律，交通数据可能会呈现重复的模式，例如每天的早晨高峰。日周期数据的目的是对交通数据的日周期性进行建模。

③
$$\begin{array}{rl}& {\mathcal{X}}_w=({\mathbf{X}}_{t_0?7?\left(T_w/T_p\right)?q+1},\dots ,{\mathbf{X}}_{t_0?7?\left(T_w/T_p\right)?q+T_p}\\ & {\mathbf{X}}_{t_0?7?\left(T_w/T_p?1\right)?q+1},\dots ,{\mathbf{X}}_{t_0?7?\left(T_w/T_p?1\right)?q+T_p},\dots \\ & {\mathbf{X}}_{t_0?7?q+1},\dots ,{\mathbf{X}}_{t_0?7?q+T_p})\in {\mathbb{R}}^{F\times N\times T_w}\end{array}$$
表示周周期时间段交通信息，长度为Tw，其中7表示一周7天。通常情况下，周一的交通模式与历史上周一的交通模式有一定的相似性，但可能与周末的交通模式有很大的不同。所以每周周期数据被设计用来捕获流量数据中的每周周期特征。

输入数据可视化表示如下

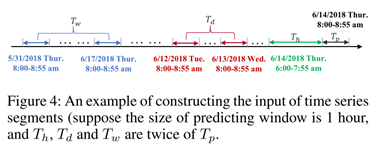
时空注意力模块

①空间注意力

首先通过${\mathbf{X}}_h^{(r?1)}=\left({\mathbf{X}}_1,{\mathbf{X}}_2,\dots {\mathbf{X}}_{T_{r?1}}\right)\in {\mathbb{R}}^{N\times C_{r?1}\times T_{r?1}}$计算出注意力矩阵S，$S_{i,j}$表示节点i与节点j的相关强度。然后通过softmax使节点注意权值之和为1。
$$\begin{array}{c}\mathbf{S}={\mathbf{V}}_s?\sigma \left(\left({\mathbf{X}}_h^{(r?1)}{\mathbf{W}}_1\right){\mathbf{W}}_2{\left({\mathbf{W}}_3{\mathcal{X}}_h^{(r?1)}\right)}^T+{\mathbf{b}}_s\right)\\ {\mathbf{S}}_{i,j}^{\prime }=\frac{\exp \left({\mathbf{S}}_{i,j}\right)}{{\sum }_{j=1}^N\exp \left({\mathbf{S}}_{i,j}\right)}\end{array}$$
其中${\mathbf{V}}_s,{\mathbf{b}}_s\in {\mathbb{R}}^{N\times N},{\mathbf{W}}_1\in {\mathbb{R}}^{T_{r?1}},{\mathbf{W}}_2\in {\mathbb{R}}^{C_{r?1}\times T_{r?1}},{\mathbf{W}}_3\in {\mathbb{R}}^{C_{r?1}}$使可学习参数。

然后注意力矩阵S’在图卷积部分将与邻接矩阵A共同调节节点间的影响权重。

②时间注意力

计算时间维度的注意力系数

$$\begin{array}{c}\mathbf{E}={\mathbf{V}}_e?\sigma \left(\left({\left({\mathcal{X}}_h^{(r?1)}\right)}^T{\mathbf{U}}_1\right){\mathbf{U}}_2\left({\mathbf{U}}_3{\mathcal{X}}_h^{(r?1)}\right)+{\mathbf{b}}_e\right)\\ {\mathbf{E}}_{i,j}^{\prime }=\frac{\exp \left({\mathbf{E}}_{i,j}\right)}{{\sum }_{j=1}^{T_{r?1}}\exp \left({\mathbf{E}}_{i,j}\right)}\end{array}$$
其中$\mathbf{V}{e{2}} \mathbf{b}{e} \in \mathbb{R}^{T{r-1} \times T_{r-1}}, \mathbf{U}{1} \in \mathbb{R}^{N}, \mathbf{U}{2} \in \mathbb{R}^{C_{r-1} \times N}, \mathbf{U}{3} \in \mathbb{R}^{C{r-1}}
$是可学习参数。

对于时间注意力块，作者直接将归一化的时间注意矩阵应用于输入，计算公式如下

$${\hat{\mathbf{X}}}_h^{(r?1)}=\left({\hat{\mathbf{X}}}_1,{\hat{\mathbf{X}}}_2,\dots ,{\hat{\mathbf{X}}}_{T_{r?1}}\right)=\left({\mathbf{X}}_1,{\mathbf{X}}_2,\dots ,{\mathbf{X}}_{T_{r?1}}\right){\mathbf{E}}^{\prime }$$
时空卷积模块

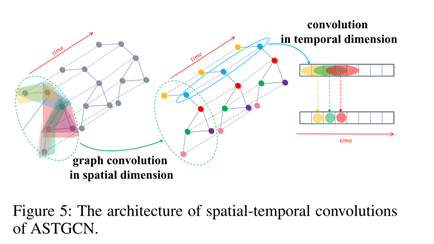
①空间维卷积

采用的是谱域方法（具体是Cheby-conv方法改进得到）。Cheby-conv计算公式如下

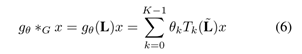
为了动态调整节点之间的相关性，对每一项的$T_k(\tilde{L})$与空间注意力矩阵$S^{\prime }\in {\mathbb{R}}^{N\times N}$进行哈达玛乘积。

具体公式如下

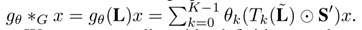
②时间维卷积

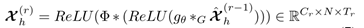
*表示标准卷积，此处应该是1D-conv，将时间点的前后数据也一起融合了一下，得到了整个模块的最终输出。

最后对三种输入得到的三种输出进行融合，公式如下

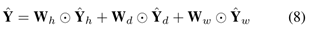
Experiments

数据使用两个加州高速数据PeMSD4和PeMSD8。

参数设置

$T_h=24,T_d=12,T_w=24$切比雪夫多项式K={1，2，3}，预测时间步长$T_p=12$

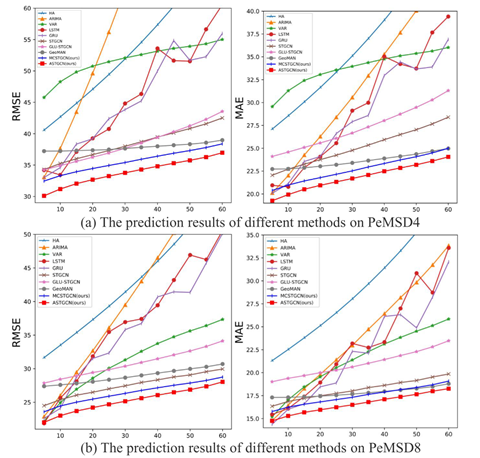
实验结果如下

MSTGCN是未使用注意力机制的模型。

下图是各种方法在预测区间增大下的影响。

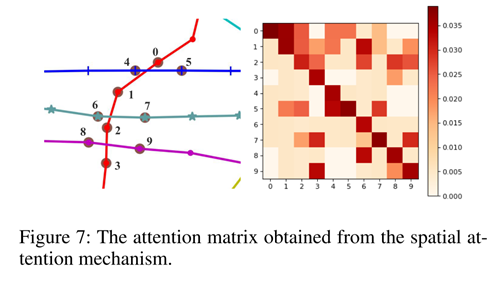
作者挑选了包含10个点的子图，并显示训练集中节点之间的平均空间注意矩阵。如下，最后一行，我们可以知道第9个点的车流与第3个点和第8个点上的车流是密切相关的。他们三个点在空间上也是相互接近的，很合理。

创新点

不仅仅使用相近时间的历史数据来预测，还考虑了同一天的同一时刻，同一周的时刻的影响来辅助预测。还有就是使用注意力直接学习时间空间相关性。