[人工智能]第五周作业：卷积神经网络（Part 3）

MobileNet V1网络

网络结构

Deep-wise卷积

MobileNets将一个标准的卷积分解为为一个深度卷积（depthwise convolutions）和一个点卷积（pointwise convolution）（1 × 1卷积核）。简单理解就是矩阵的因式分解。深度卷积将每个卷积核应用到每一个通道，而1 × 1卷积用来组合通道卷积的输出，这种分解可以有效减少计算量，降低模型大小。
卷积过程说明：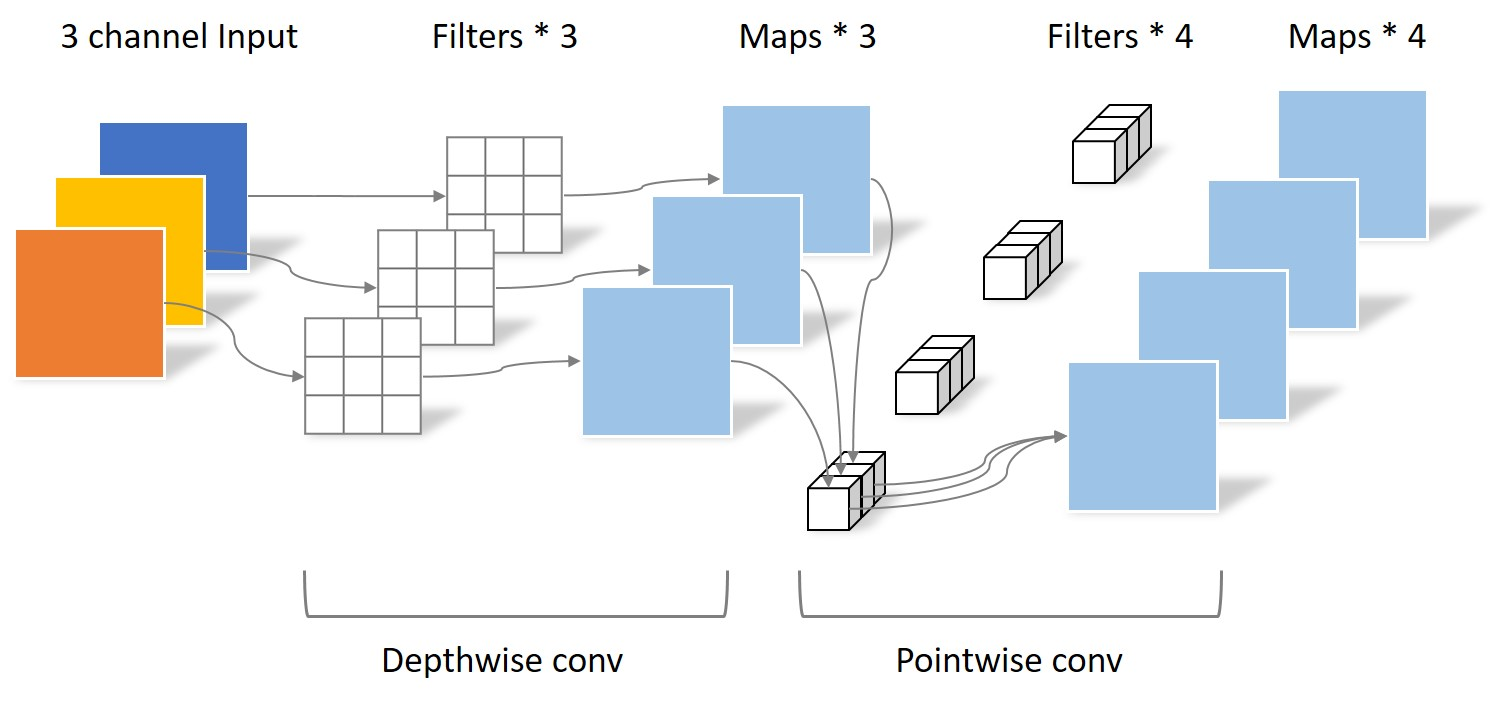

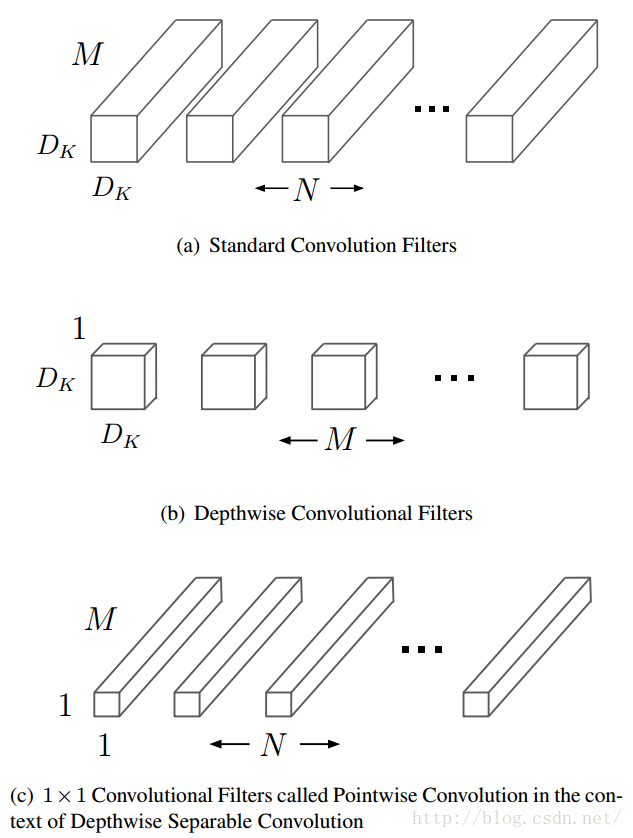
传统的3D卷积使用一个和输入数据通道数相同的卷积核在逐个通道卷积后求和最后得出一个数值作为结果，计算量为$$M\times D_k\times D_k$$其中M为输入的通道数，D_k 为卷积核的宽和高。
一个卷积核处理输入数据时的计算量为（有Padding）：$$D_k\times D_k\times M\times D_F\times D_F$$其中DF为输入的宽和高。
在某一层如果使用N个卷积核，这一个卷积层的计算量为：$$D_k\times D_k\times N\times M\times D_F\times D_F$$
如果使用deep-wise方式的卷积核，我们会首先使用一组二维的卷积核，也就是卷积核的通道数为1，每次只处理一个输入通道的，这一组二维卷积核的数量是和输入通道数相同的。在使用逐个通道卷积处理之后，再使用3D的1×1卷积核来处理之前输出的特征图，将最终输出通道数变为一个指定的数量。
一组和输入通道数相同的2D卷积核的运算量为：$$D_k\times D_k\times M\times D_F\times D_F$$
3D的1×1卷积核的计算量为：$$N\times M\times D_F\times D_F$$
因此这种组合方式的计算量为：$$D_k\times D_k\times M\times D_F\times D_F+N\times M\times D_F\times D_F$$
deep-wise方式的卷积相比于传统3D卷积计算量为：
$$\frac{D_k\times D_k\times M\times D_F\times D_F+N\times M\times D_F\times D_F}{D_k\times D_k\times N\times M\times D_F\times D_F}=\frac{1}{N}+\frac{1}{D_k^2}$$

网络结构

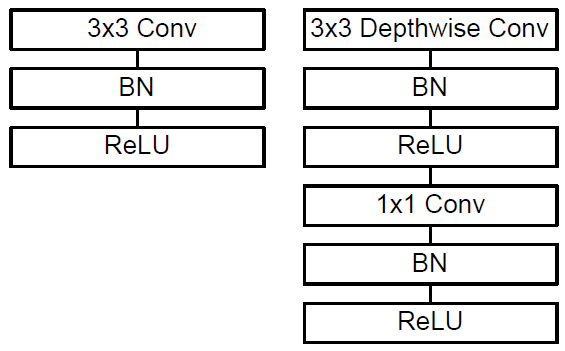
从图中可以看出，deep-wise的卷积和后面的1×1卷积被当成了两个独立的模块，都在输出结果的部分加入了Batch Normalization和非线性激活单元。
Deep-wise结合1×1的卷积方式代替传统卷积不仅在理论上会更高效，而且由于大量使用1×1的卷积，可以直接使用高度优化的数学库来完成这个操作。

MobileNet V2网络

相比V1的两点改进

Linear Bottlenecks

V1中使用width multiplier参数来做模型通道的缩减，使特征信息集中在缩减后的通道中，其后使用非线性激活ReLU，会产生较大的信息丢失。为了减少信息损失，V2使用linear bottleneck，在bottleneck的输出后接线性激活。

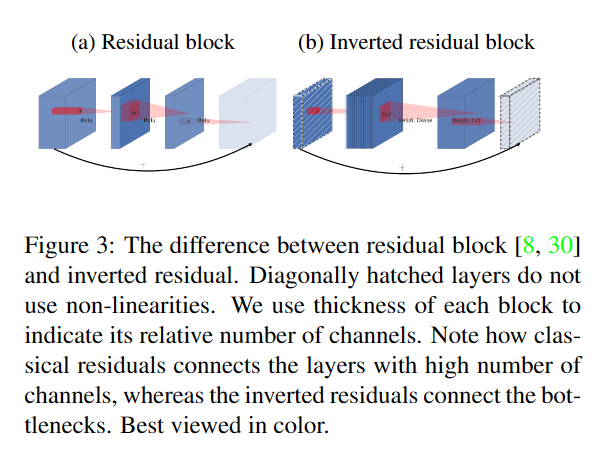
Inverted residuals

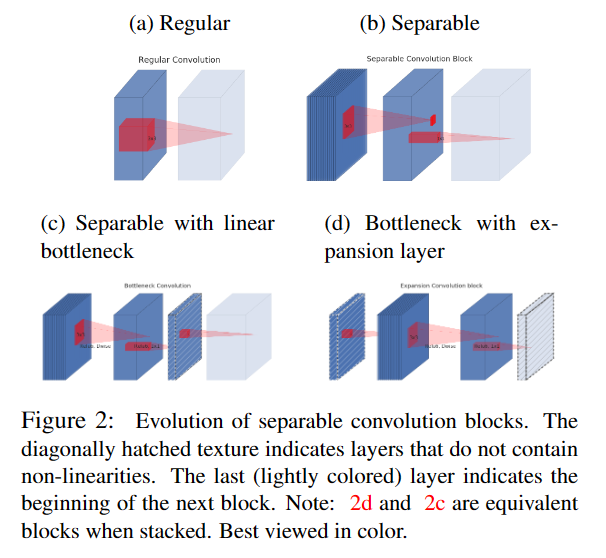
Figure2展示了从standard convolution到depthwise separable convolution再到本文中的inverted residual block的差异。
(a) 标准3×3卷积操作，若输入channel数量为n，则卷积核的维度为3×3×n(图中红色立方体)，将channel和spatial的信息同时进行映射，参数量较大；
(b) V1中采用的depthwise separable convolution，可分离卷积，解耦了channel和spatial，化乘法为加法；
? 在(b)的基础上增加了一个类似bottleneck的操作；
(d) V2 inverted residual block结构，和ResNet中residual block对维度的操作相反。

HybridSN 高光谱分类网络

论文信息

论文：HybridSN: Exploring 3-D–2-DCNN Feature Hierarchy for Hyperspectral Image Classification

网络结构

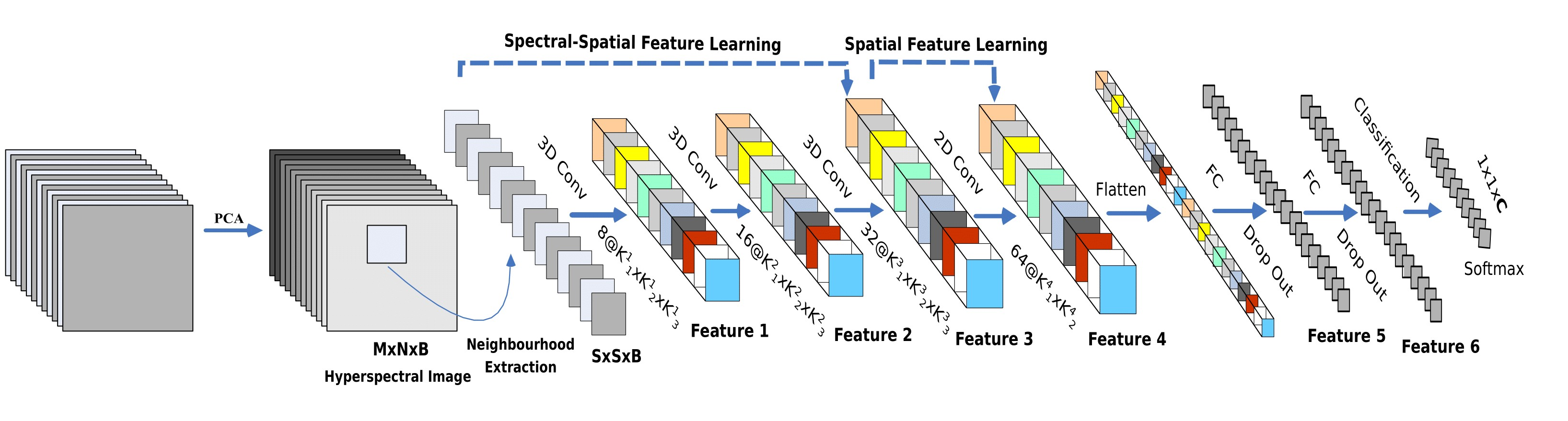
由上图，网络依次由3层三维卷积(3D Conv) → 1层二维卷积(2D Conv) → 2层全连接层(Fc) → 1层softmax分类层组成。
三维卷积：
conv1：（1, 30, 25, 25）， 8个 7x3x3 的卷积核 -->（8, 24, 23, 23）
conv2：（8, 24, 23, 23）， 16个 5x3x3 的卷积核 -->（16, 20, 21, 21）
conv3：（16, 20, 21, 21），32个 3x3x3 的卷积核 -->（32, 18, 19, 19）
二维卷积：
把前面的 32*18 reshape 一下，得到 （576, 19, 19），64个 3x3 的卷积核 --> （64, 17, 17），
接下来是一个 flatten 操作，变为 18496 维的向量，
接下来依次为256，128节点的全连接层，都使用比例为0.4的 Dropout，
最后输出为 16 个节点，是最终的分类类别数。

代码：

class_num = 16
class HybridSN(nn.Module):
  def __init__(self):
    super(HybridSN, self).__init__()
    self.conv3d_1 = nn.Sequential(
        nn.Conv3d(1, 8, kernel_size=(7, 3, 3), stride=1, padding=0),
        nn.BatchNorm3d(8),
        nn.ReLU(inplace = True),
    )
    self.conv3d_2 = nn.Sequential(
        nn.Conv3d(8, 16, kernel_size=(5, 3, 3), stride=1, padding=0),
        nn.BatchNorm3d(16),
        nn.ReLU(inplace = True),
    ) 
    self.conv3d_3 = nn.Sequential(
        nn.Conv3d(16, 32, kernel_size=(3, 3, 3), stride=1, padding=0),
        nn.BatchNorm3d(32),
        nn.ReLU(inplace = True)
    )

    self.conv2d_4 = nn.Sequential(
        nn.Conv2d(576, 64, kernel_size=(3, 3), stride=1, padding=0),
        nn.BatchNorm2d(64),
        nn.ReLU(inplace = True),
    )
    self.fc1 = nn.Linear(18496,256)
    self.fc2 = nn.Linear(256,128)
    self.fc3 = nn.Linear(128,16)
    self.dropout = nn.Dropout(p = 0.4)

  def forward(self,x):
    out = self.conv3d_1(x)
    out = self.conv3d_2(out)
    out = self.conv3d_3(out)
    out = self.conv2d_4(out.reshape(out.shape[0],-1,19,19))
    out = out.reshape(out.shape[0],-1)
    out = F.relu(self.dropout(self.fc1(out)))
    out = F.relu(self.dropout(self.fc2(out)))
    out = self.fc3(out)
    return out

结果：

          precision    recall  f1-score   support

     0.0     1.0000    0.9024    0.9487        41
     1.0     0.9959    0.9447    0.9696      1285
     2.0     0.9570    0.9839    0.9703       747
     3.0     0.9364    0.9671    0.9515       213
     4.0     0.9742    0.9540    0.9640       435
     5.0     0.9864    0.9954    0.9909       657
     6.0     1.0000    0.9600    0.9796        25
     7.0     0.9795    0.9977    0.9885       430
     8.0     0.7500    0.8333    0.7895        18
     9.0     0.9674    0.9840    0.9756       875
    10.0     0.9702    0.9878    0.9789      2210
    11.0     0.9741    0.9157    0.9440       534
    12.0     0.9836    0.9730    0.9783       185
    13.0     0.9939    0.9974    0.9956      1139
    14.0     0.9773    0.9942    0.9857       347
    15.0     0.8202    0.8690    0.8439        84

accuracy                           0.9752    9225
macro avg      0.9541    0.9537    0.9534    9225
weighted avg   0.9756    0.9752    0.9751    9225
准确率：97.52%

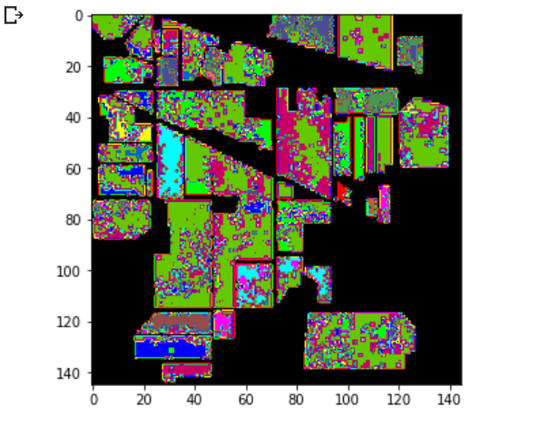
训练网络，然后多测试几次，会发现每次分类的结果都不一样，请思考为什么？

Dropout随机丢弃神经元，导致训练结果偏差。