文章目录
空间滤波基础
模板卷积
模板操作是数字图像处理中常用的一种邻域运算方式,主要有卷积和相关两种, 可以实现图像平滑、 图像锐化、边缘检测等功能。
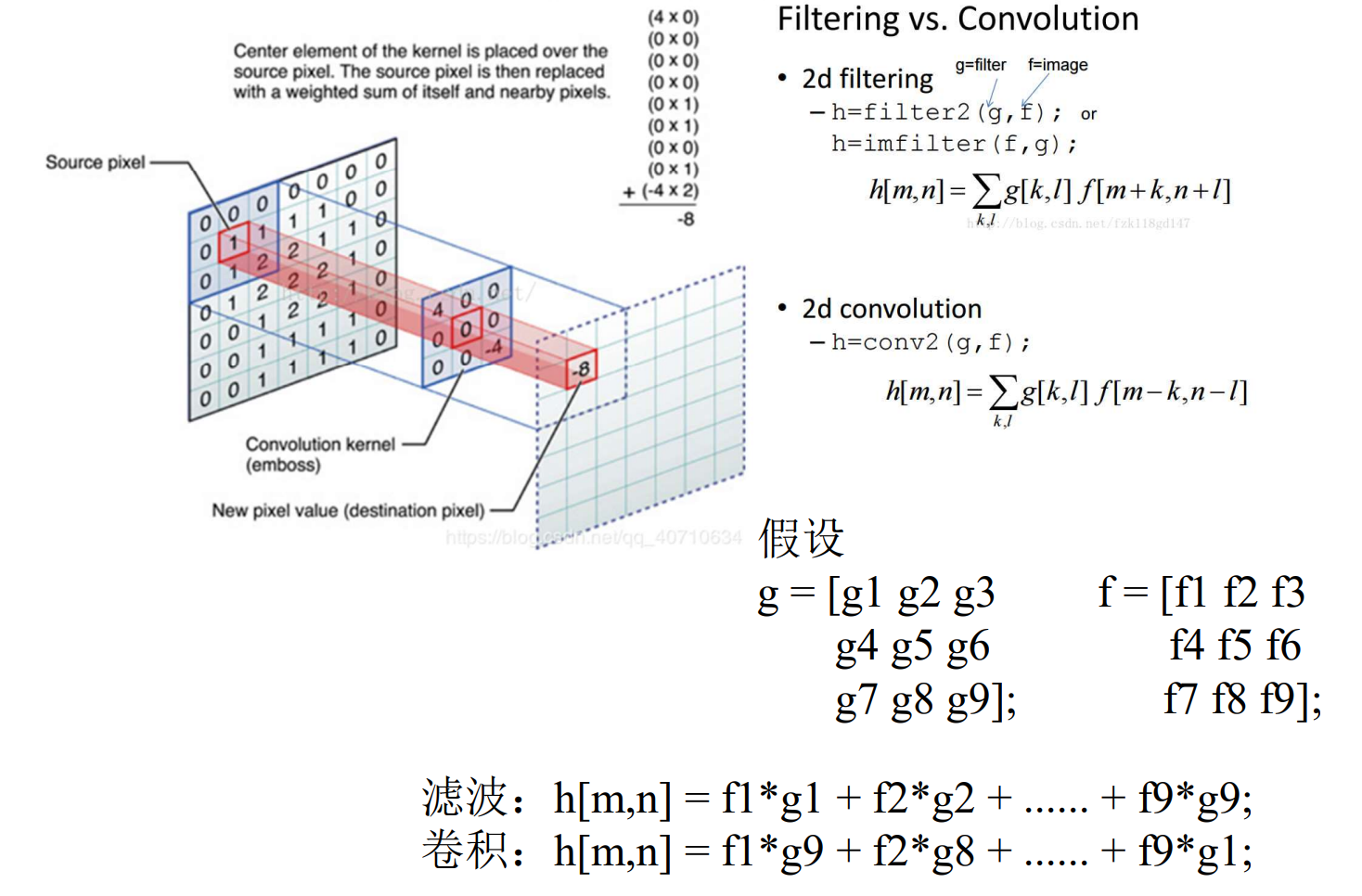
模板卷积(或相关)是指模板与图像进行卷积(或相关)运算, 是一种线性滤波, 其输出像素是输入邻域像素的线性加权和。 模板卷积和相关分别定义为

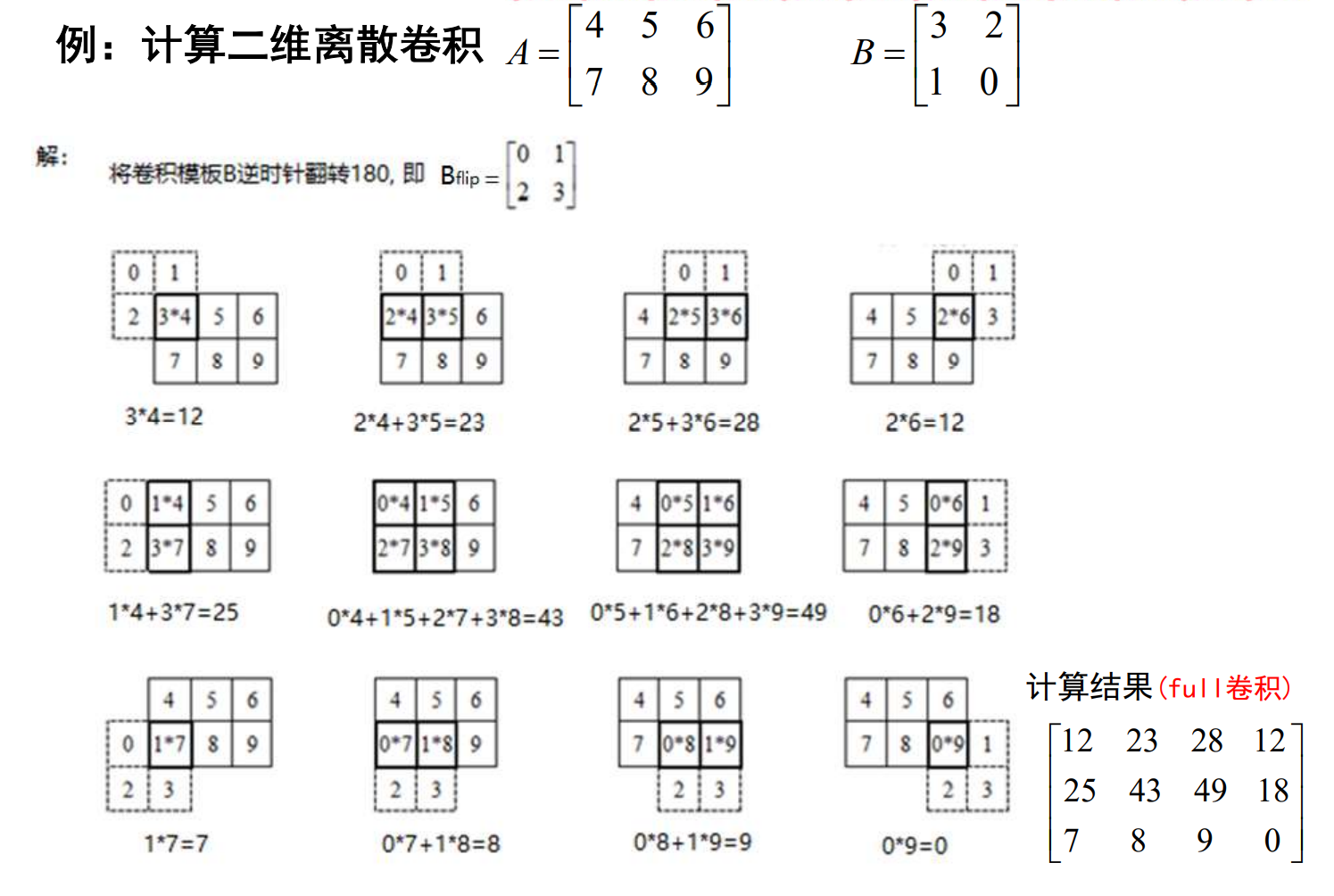
计算二维离散卷积
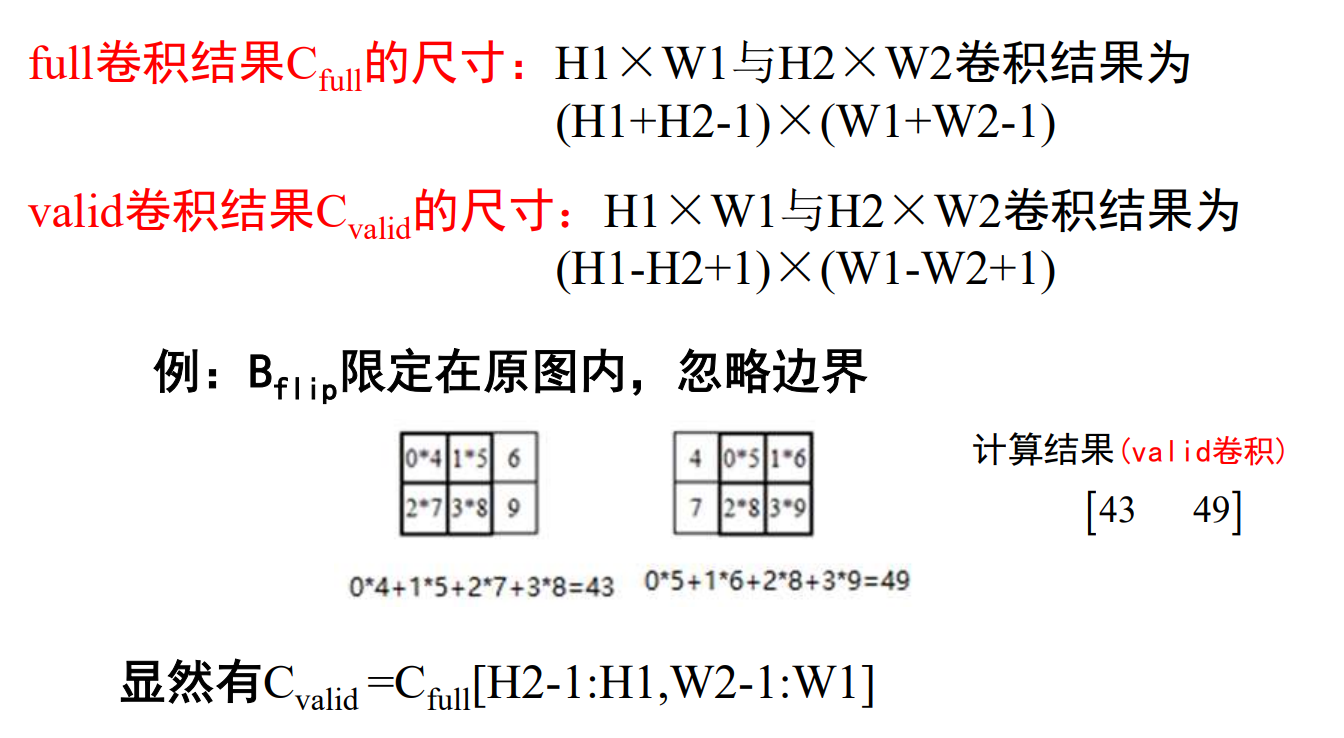
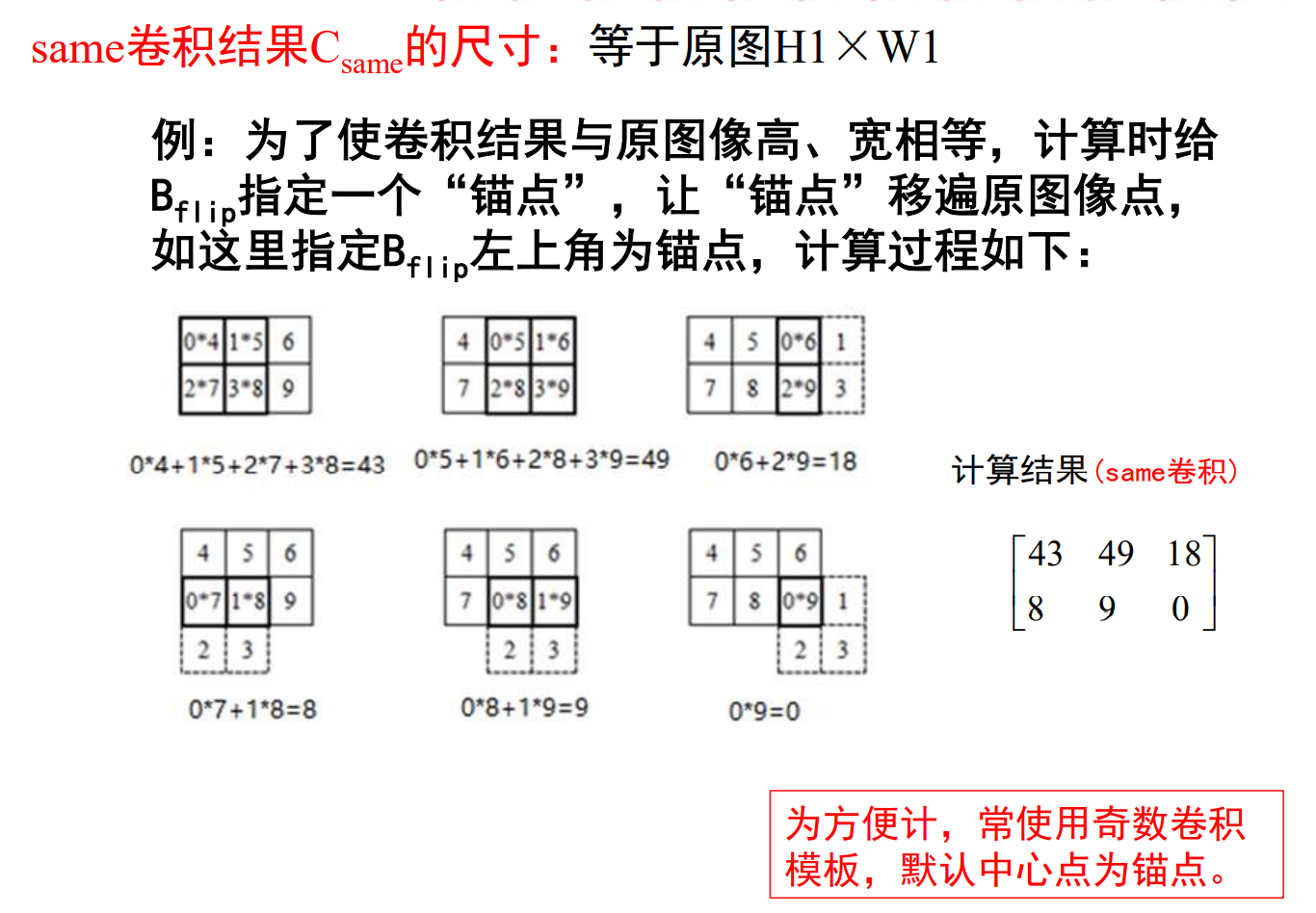
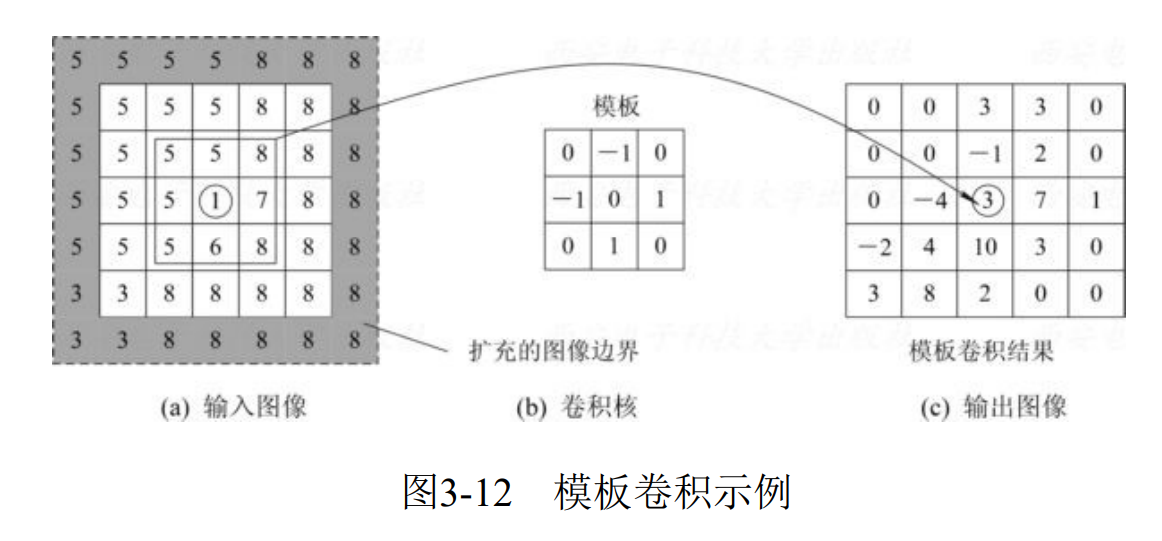
模板操作时,图像边界问题处理:
1)不处理;
2)复制边界像素扩充图像;
3)常数填充扩充图像边界。
卷积是可交换的
互相关函数和卷积运算几乎一样但是并没有对核进行翻转
许多机器学习的库实现的是互相关函数但是称之为卷积
图像平滑
平滑技术是为了减少图像的噪声。一般情况下,在空域内用邻域平均减少噪声;在频域内用低通滤波来减少噪声
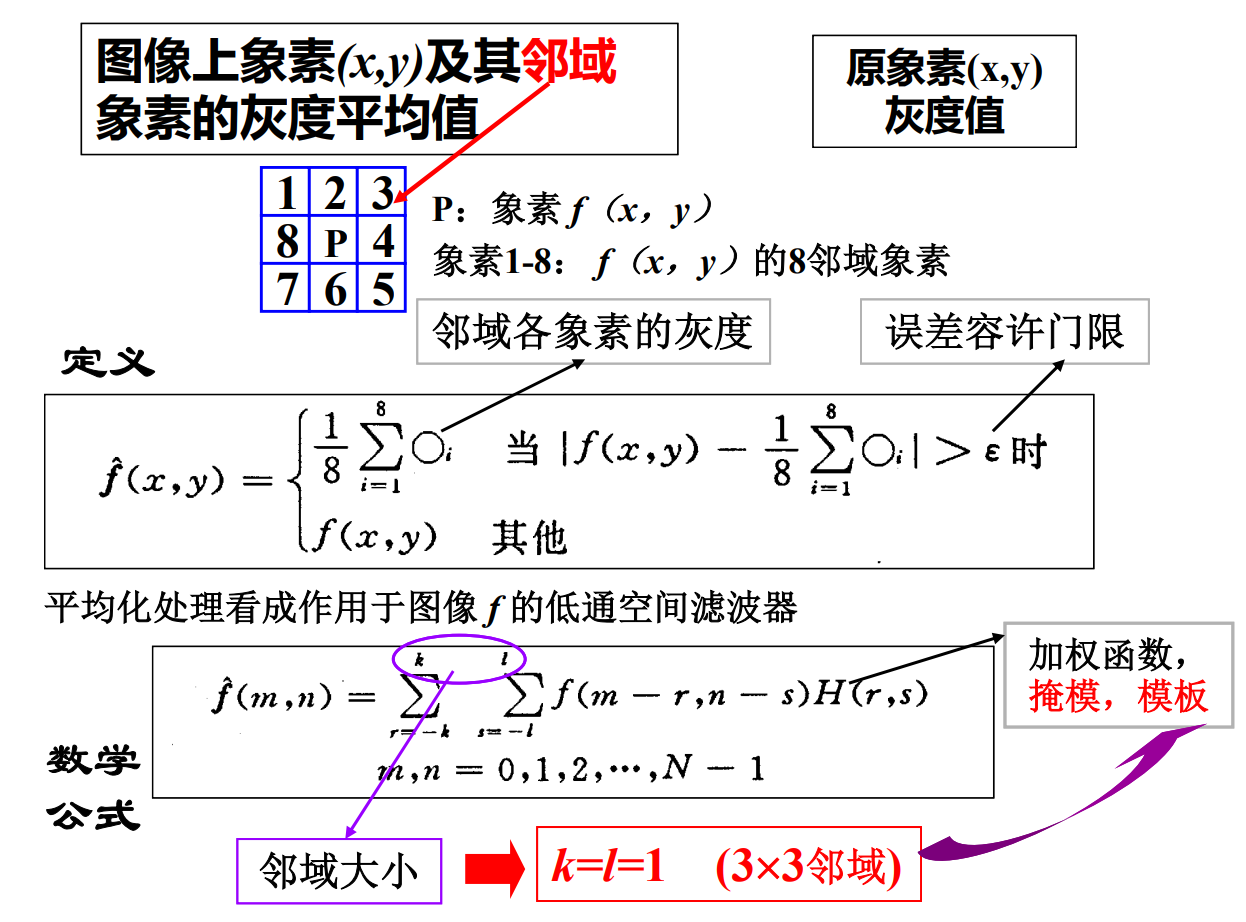
加权平均模板操作
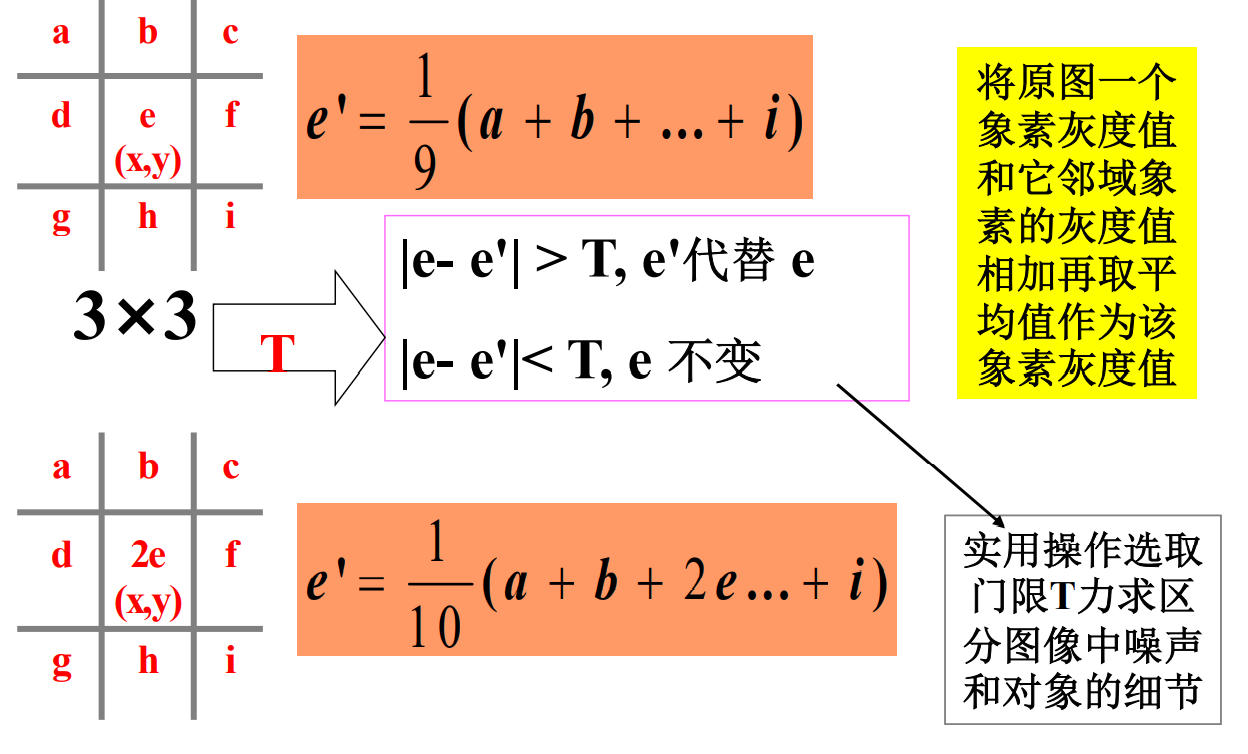
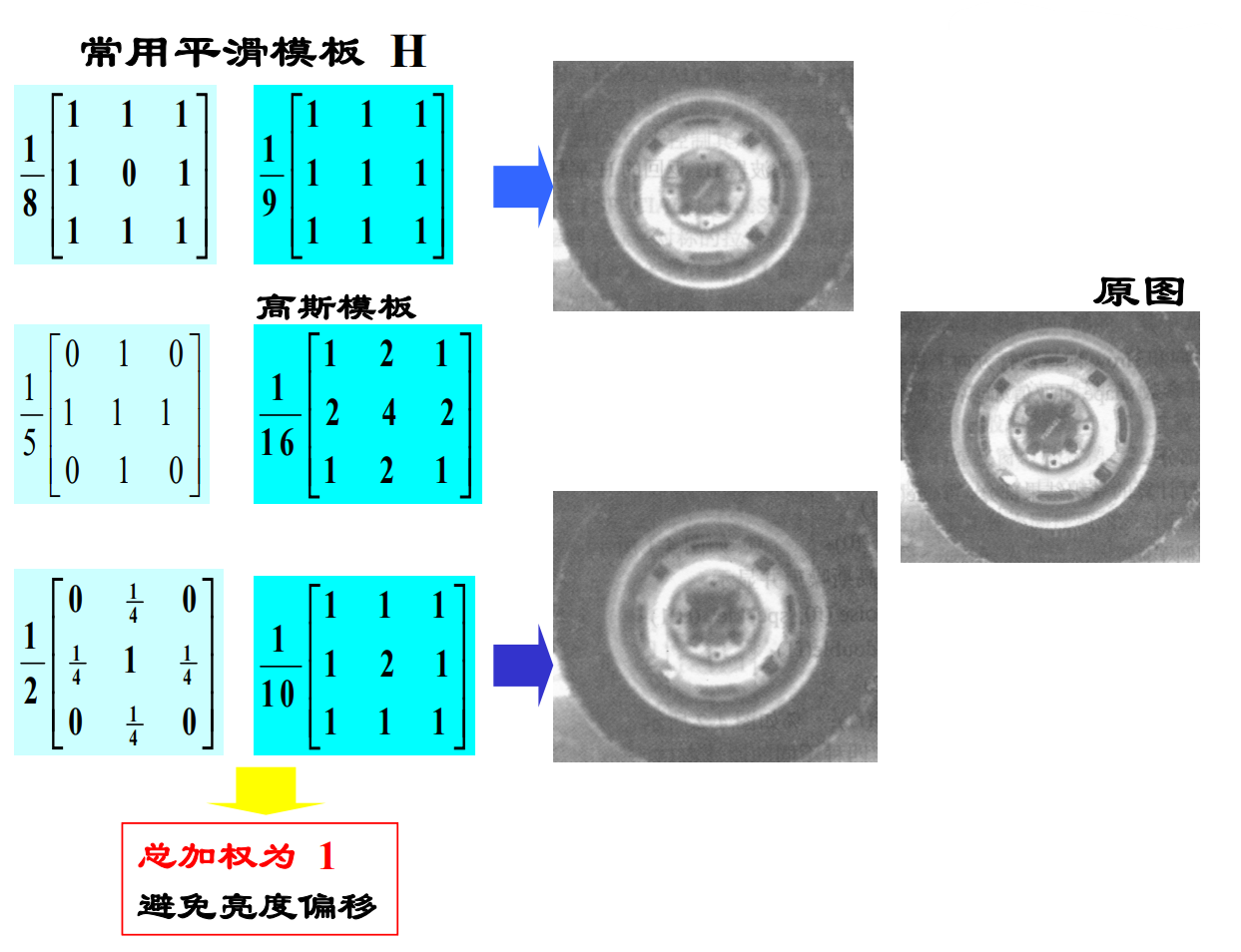
注意

并行处理特点
平滑过程不受操作顺序影响,但输入输出图像需分别设置数组
串行处理特点
平滑过程受操作顺序影响,但输入输出图像只需设置一个数组,节省内存
中值滤波法
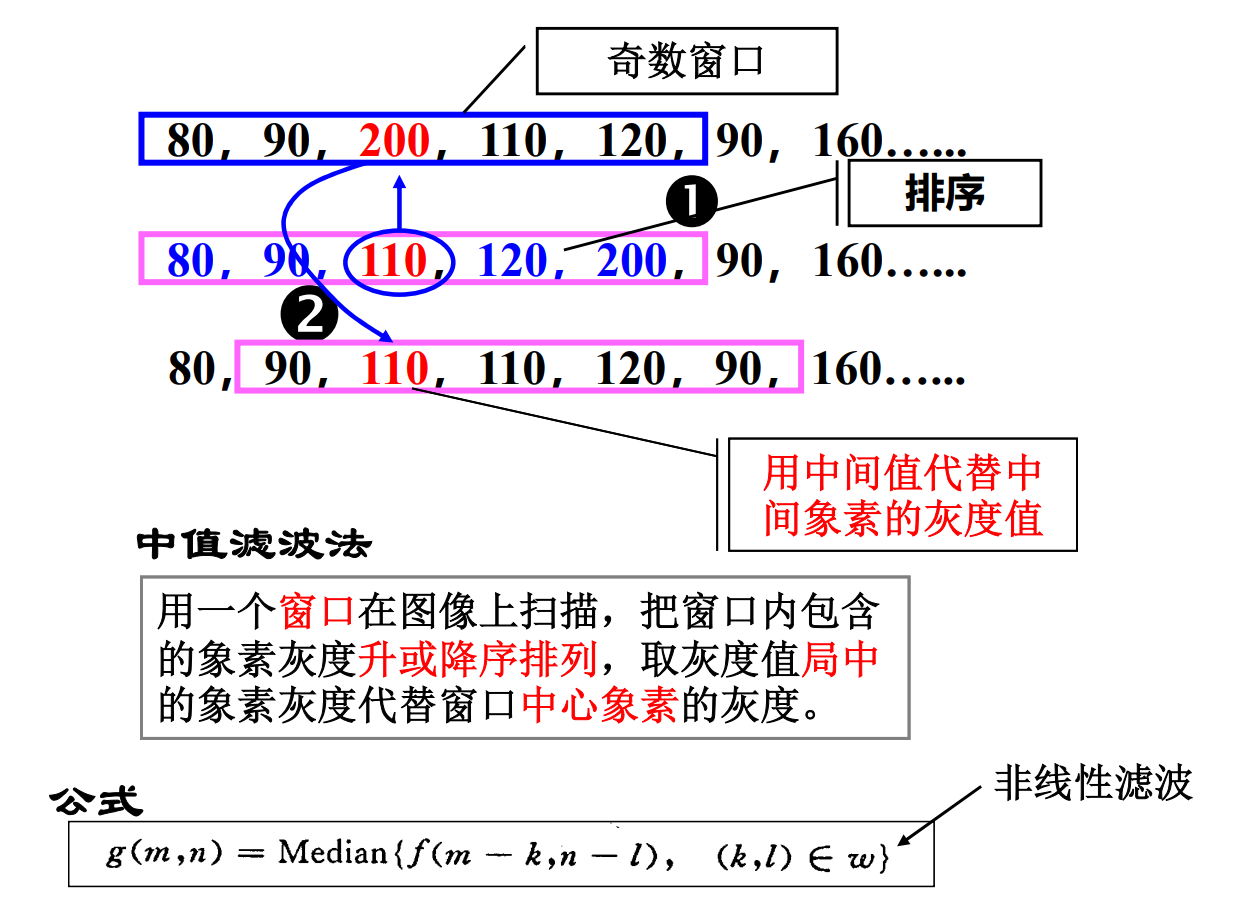
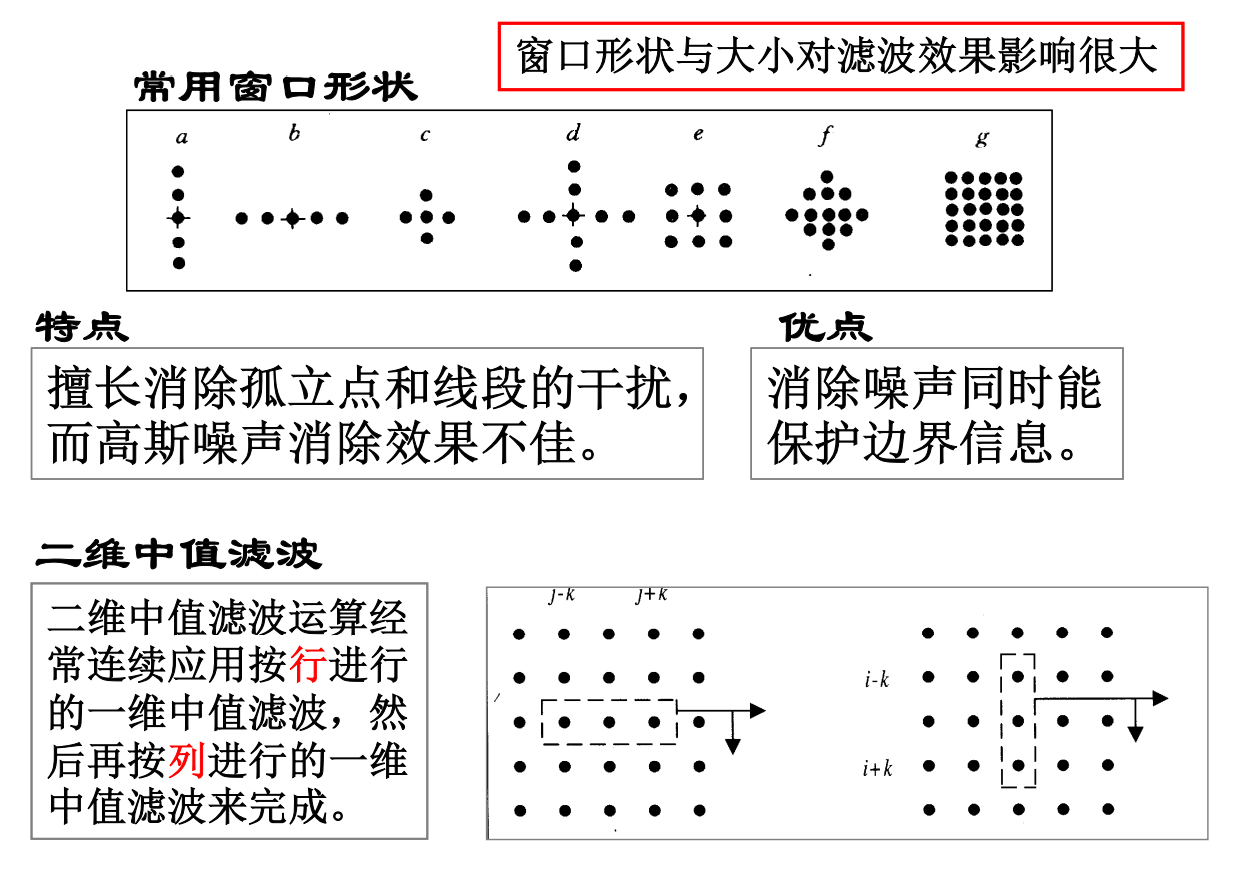
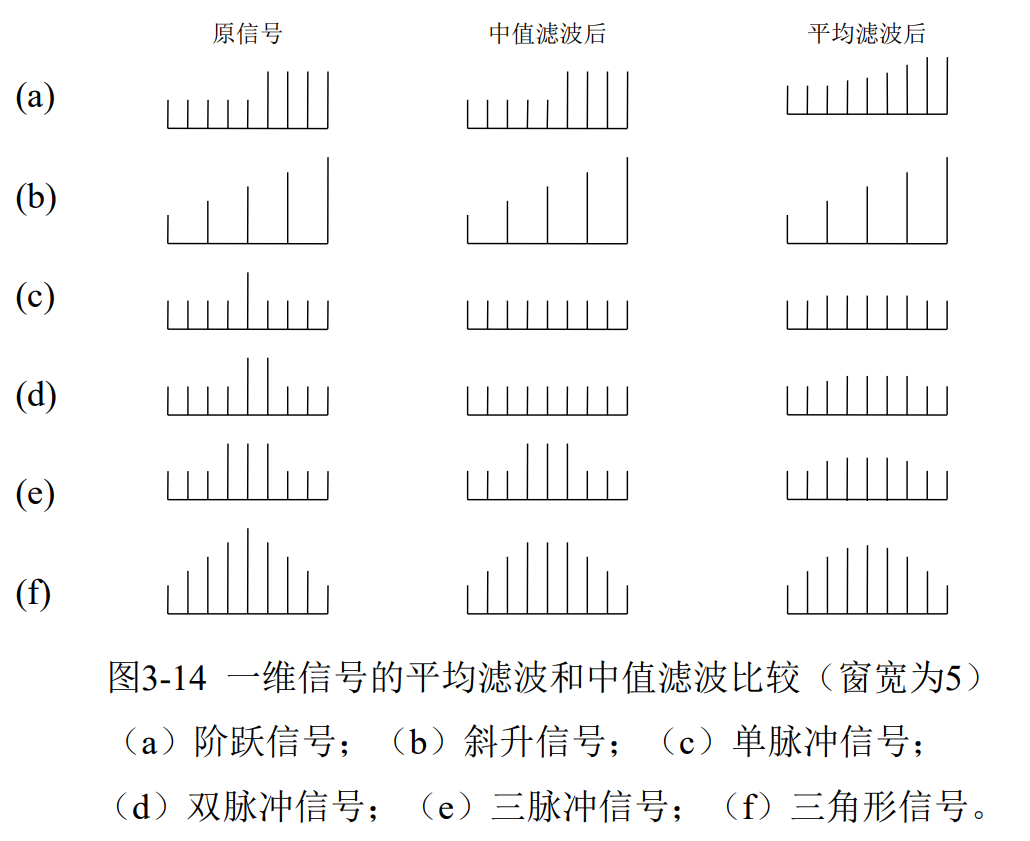

对一些内容复杂的图像, 可以使用复合型中值滤波。
复合型中值滤波:中值滤波线性组合、 高阶中值滤波组合、 加权中值滤波以及迭代中值滤波等
中值滤波的线性组合: 几种窗口尺寸大小和形状不同的中值滤波器复合使用

多图像平均法
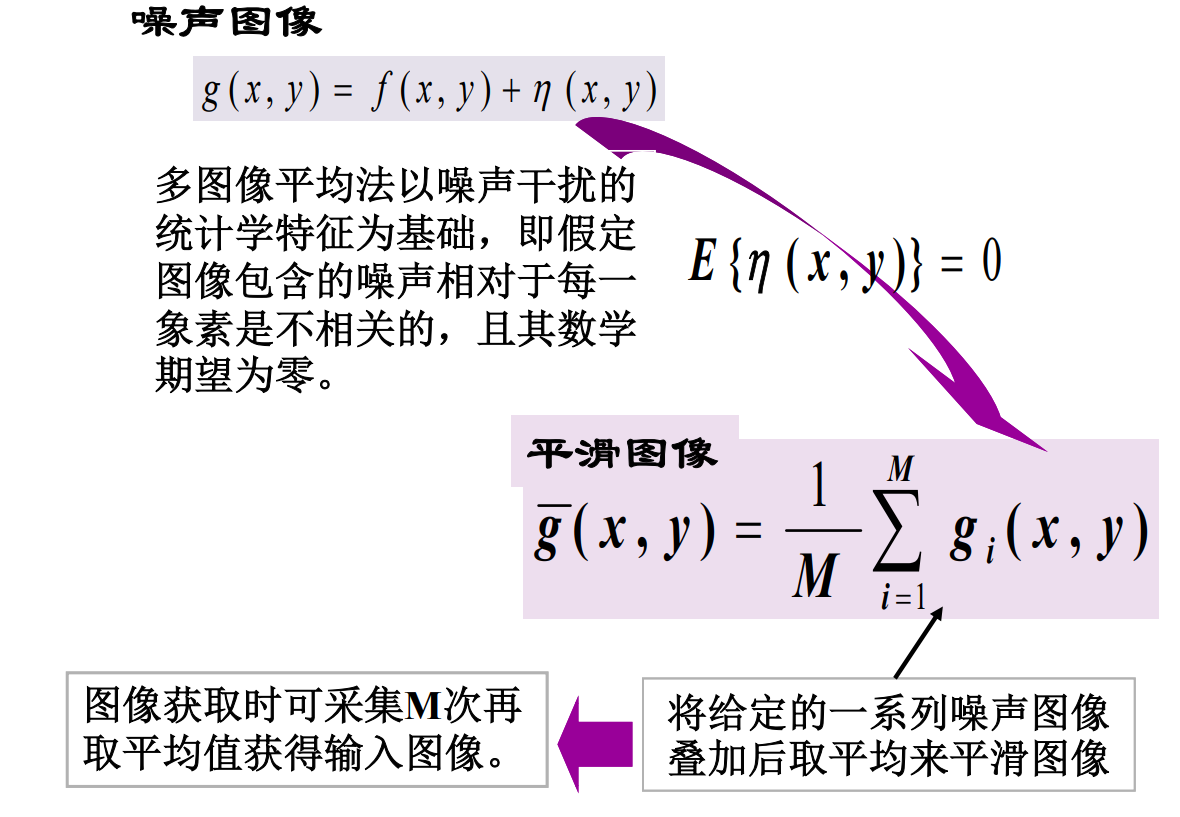
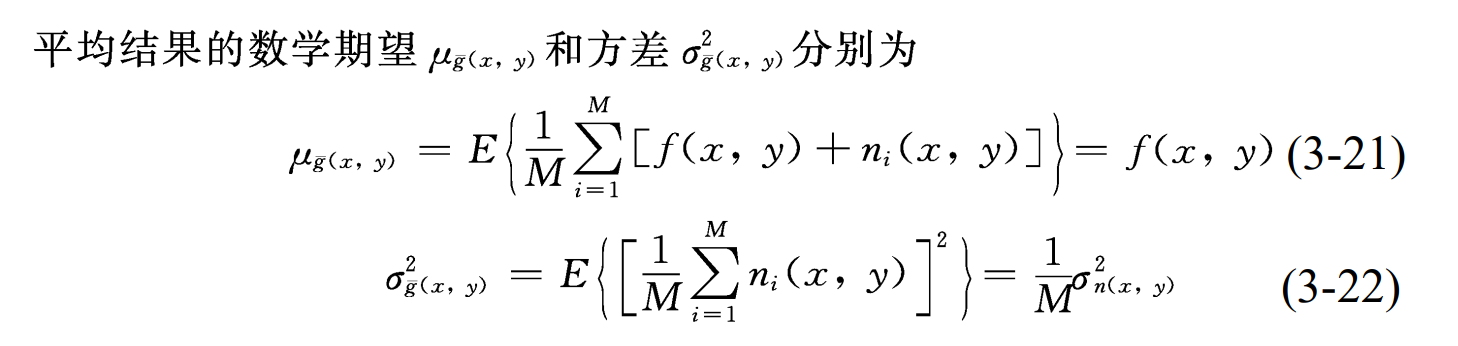
由此可见, 图像平均后可使噪声方差减少M倍, 即当M增大时平均结果将更加接近理想图像。 图像平均法常用于摄像机的视频图像中, 用以减少光电摄像管或CCD器件所引起的噪声。图像平均的难点在于多幅图像之间的配准, 实际操作困难

图像锐化
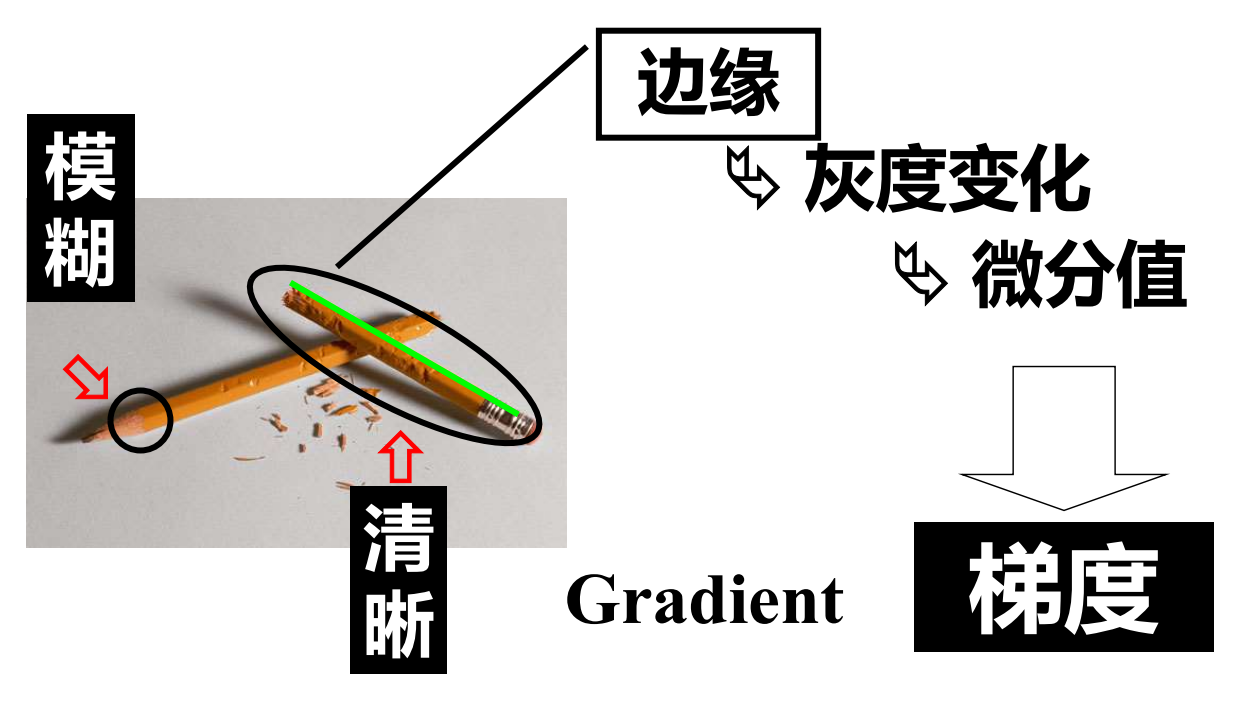
锐化技术是为了突出边缘,加强轮廓特征。在空域内用微分法使图像清晰;在频域内用高通滤波来清晰图像。
图像模糊是图像受到平均或积分运算造成,可对图像进行逆运算来使图像清晰化。
图像模糊是其高频分量被衰减,利用图像变换对图像进行频域变换,再对高频谱进行修正,再将修正后图像反变换回空域中。
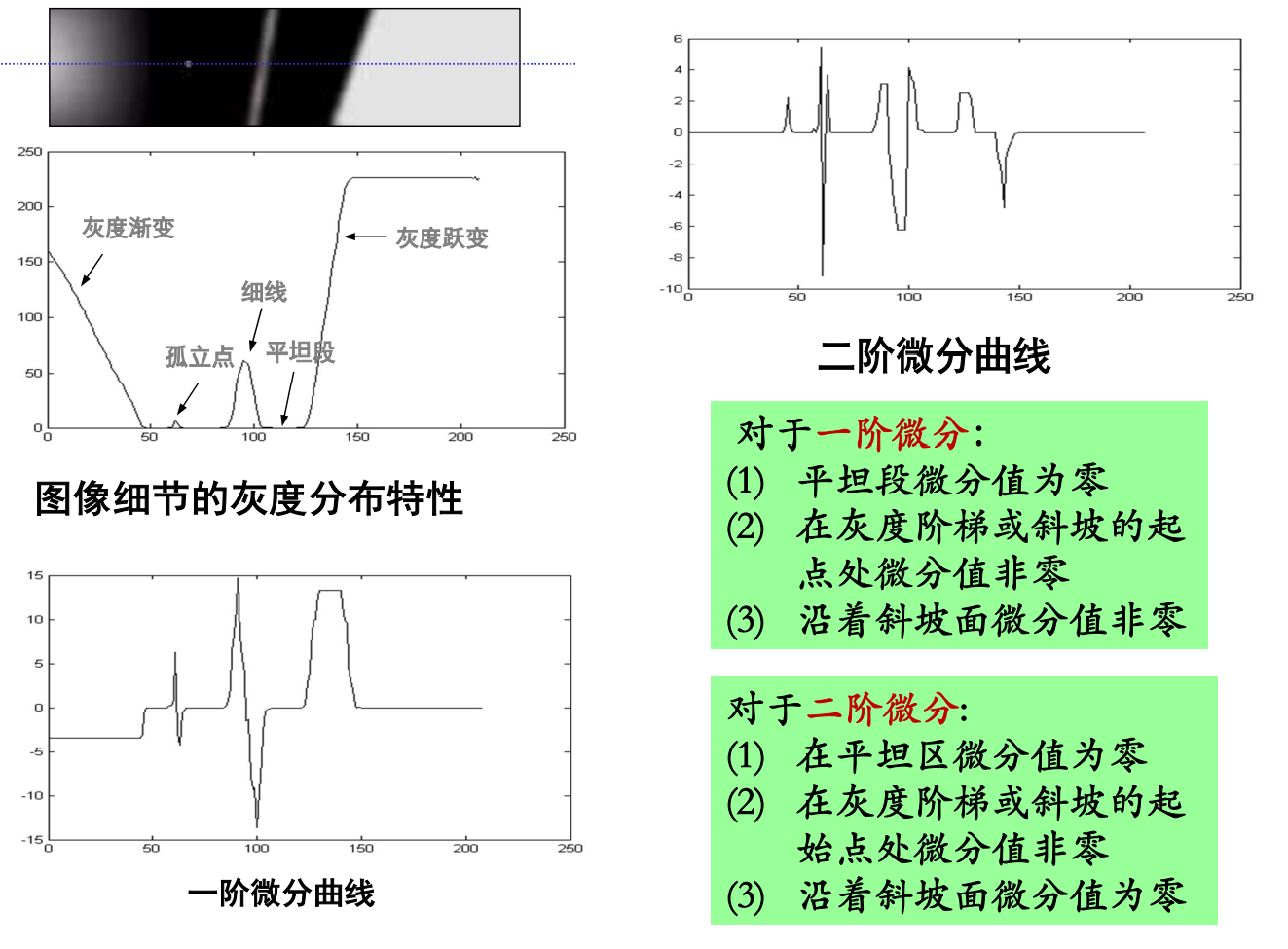
一阶微分和二阶微分的区别
(1)一阶微分处理通常会产生较宽的边缘,二阶微分处理得到的边缘则细。
(2)二阶微分处理对细节有较强的响应,如细线和孤立点
(3)一阶微分处理一般对灰度阶梯有较强的响应
(4)二阶微分处理对灰度级阶梯变化产生双响应
(5)二阶微分在图像中灰度值变化相似时,对线的响应要比对阶梯强,且点比线强.
大多数应用中,对图像增强来说.二阶微分处理比一阶微分好,因为形成细节的能力强. 而一阶微分处理主要用于提取边缘
图像细节的灰度变化特性
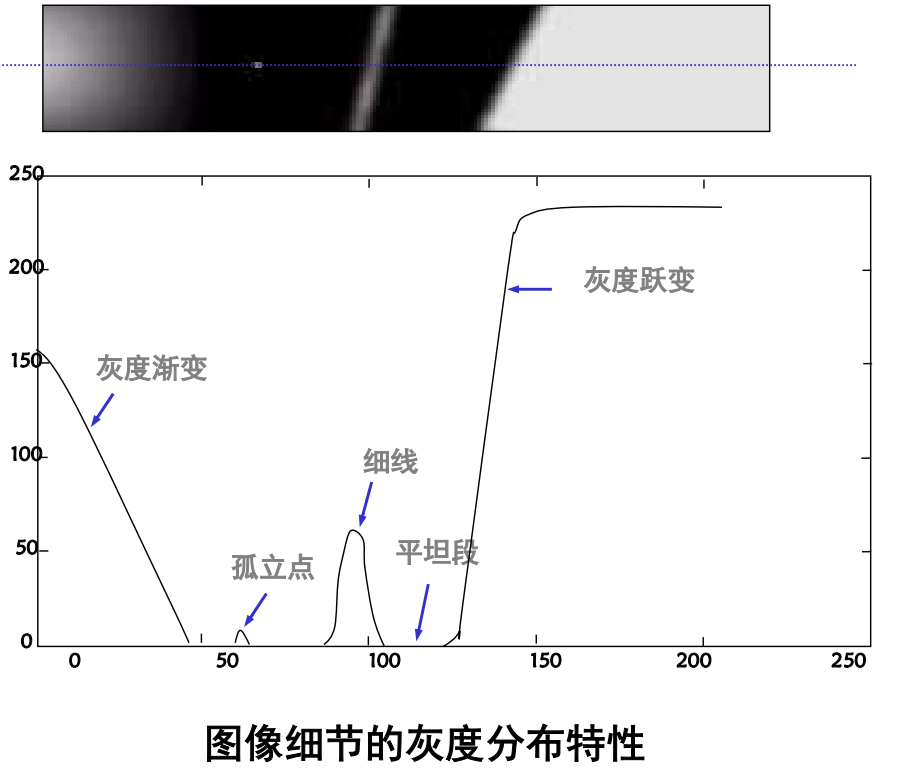
图像细节的灰度变化微分特性




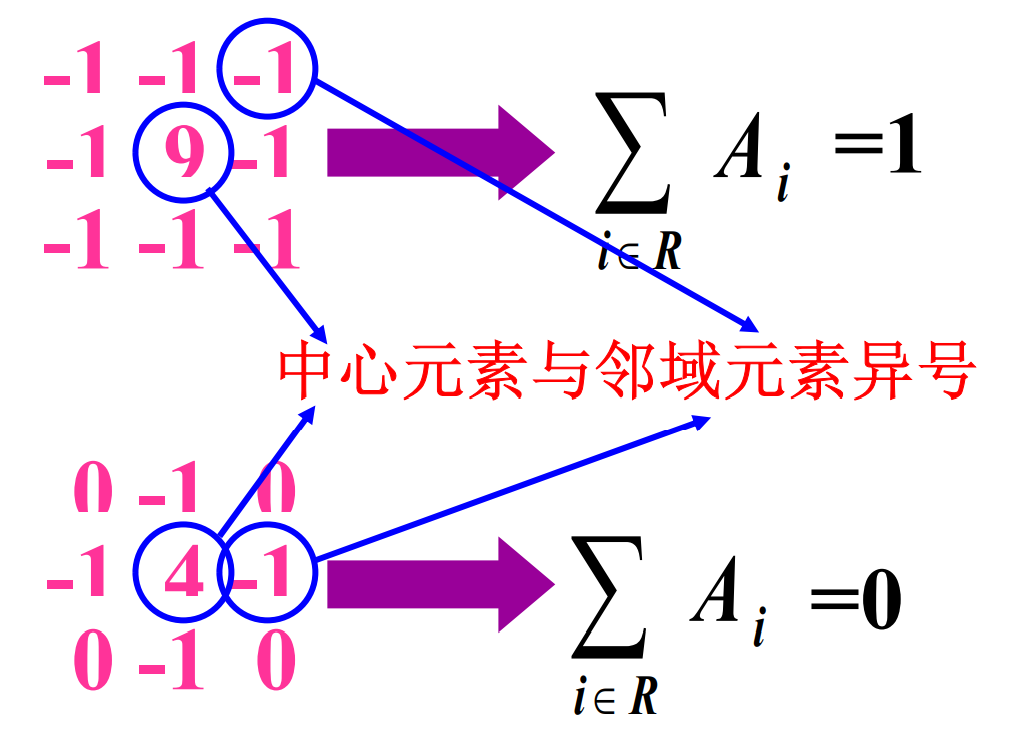
拉普拉斯锐化

锐化模板设计特点
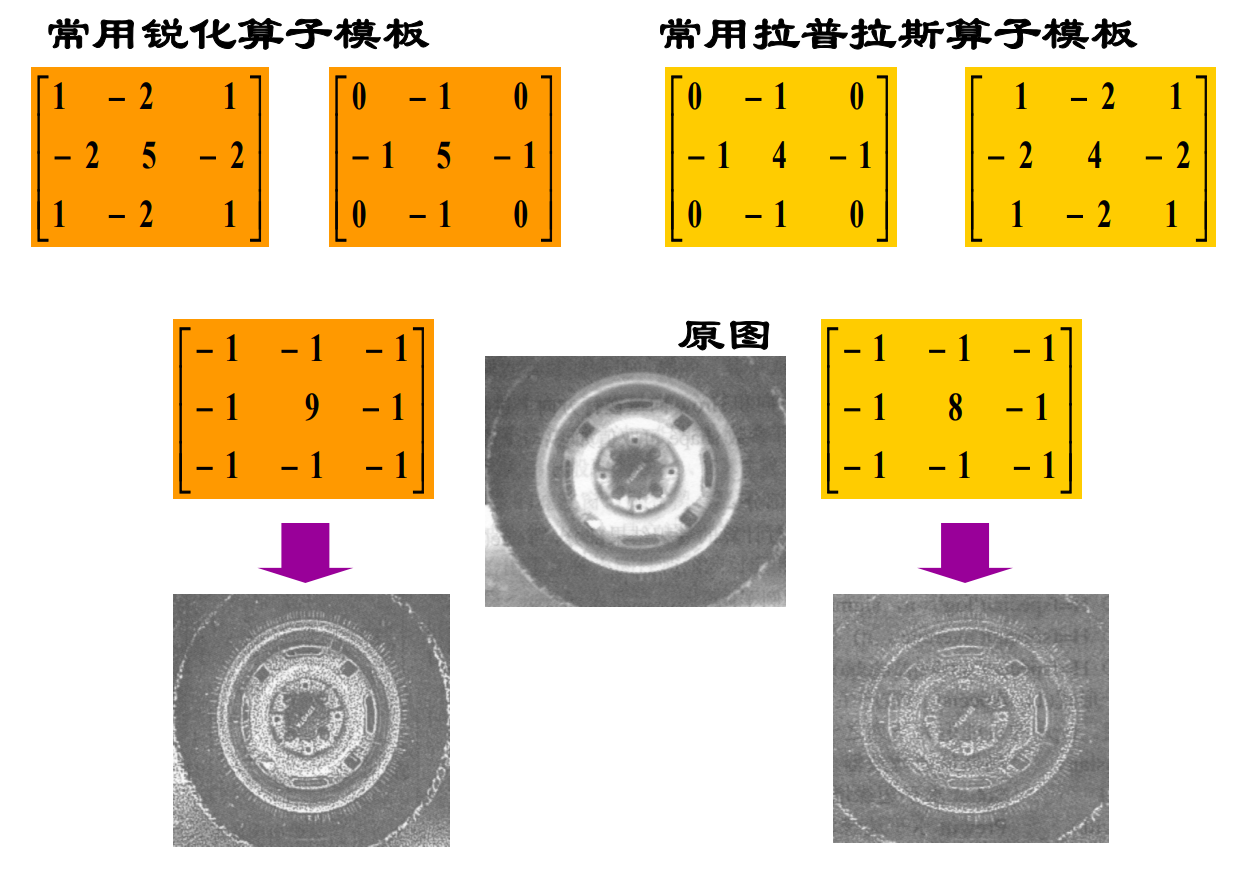
空域图像线性滤波技术 综合实例
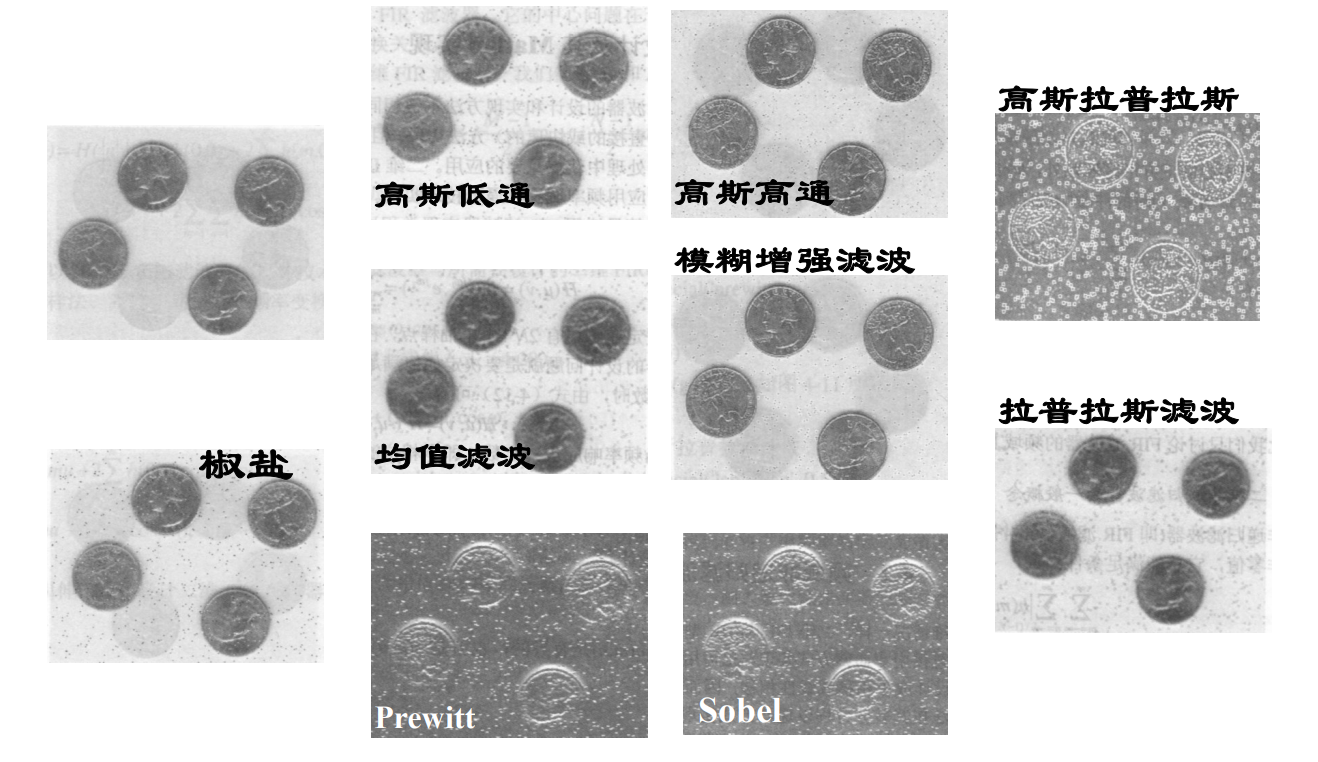
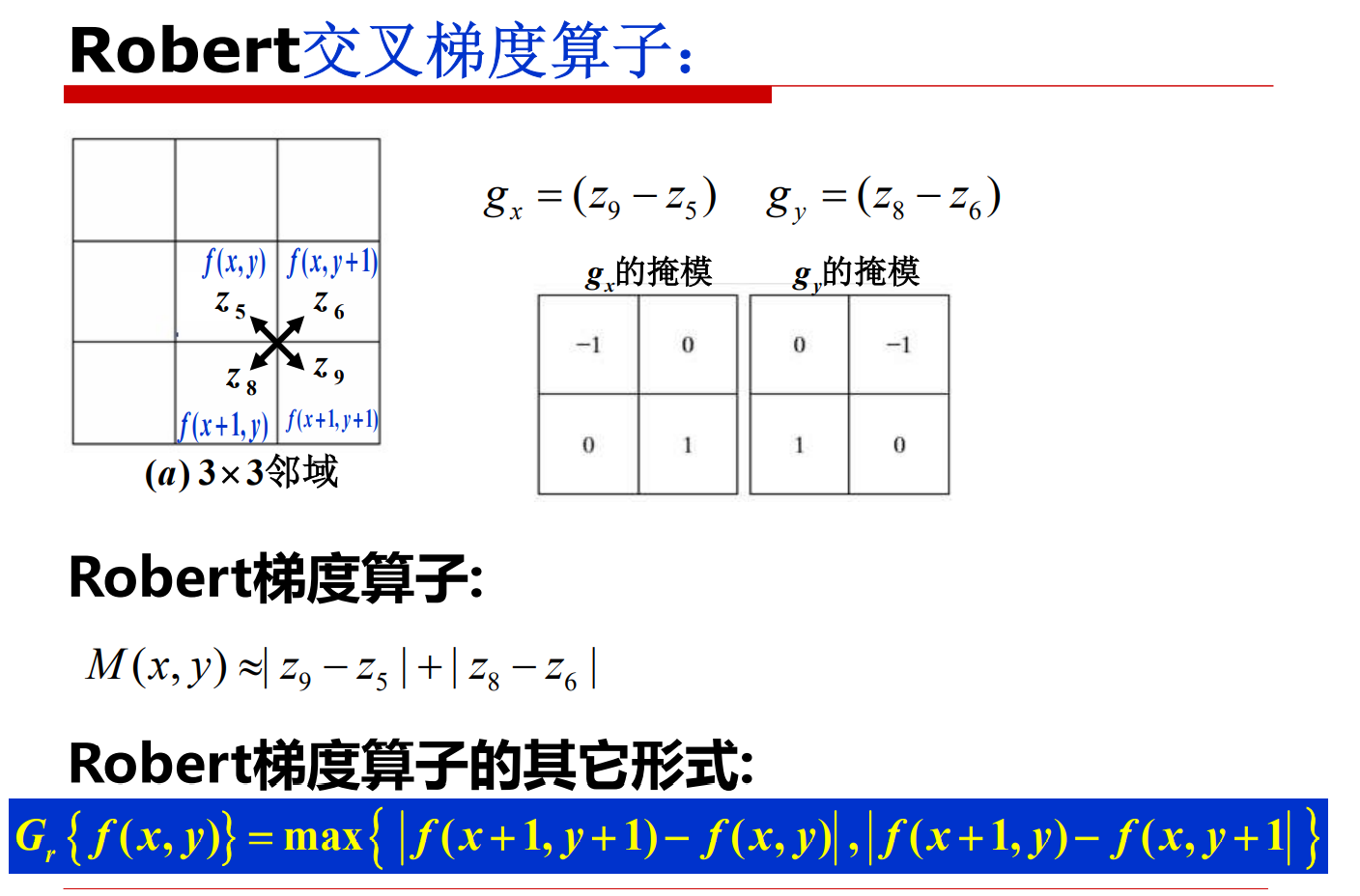
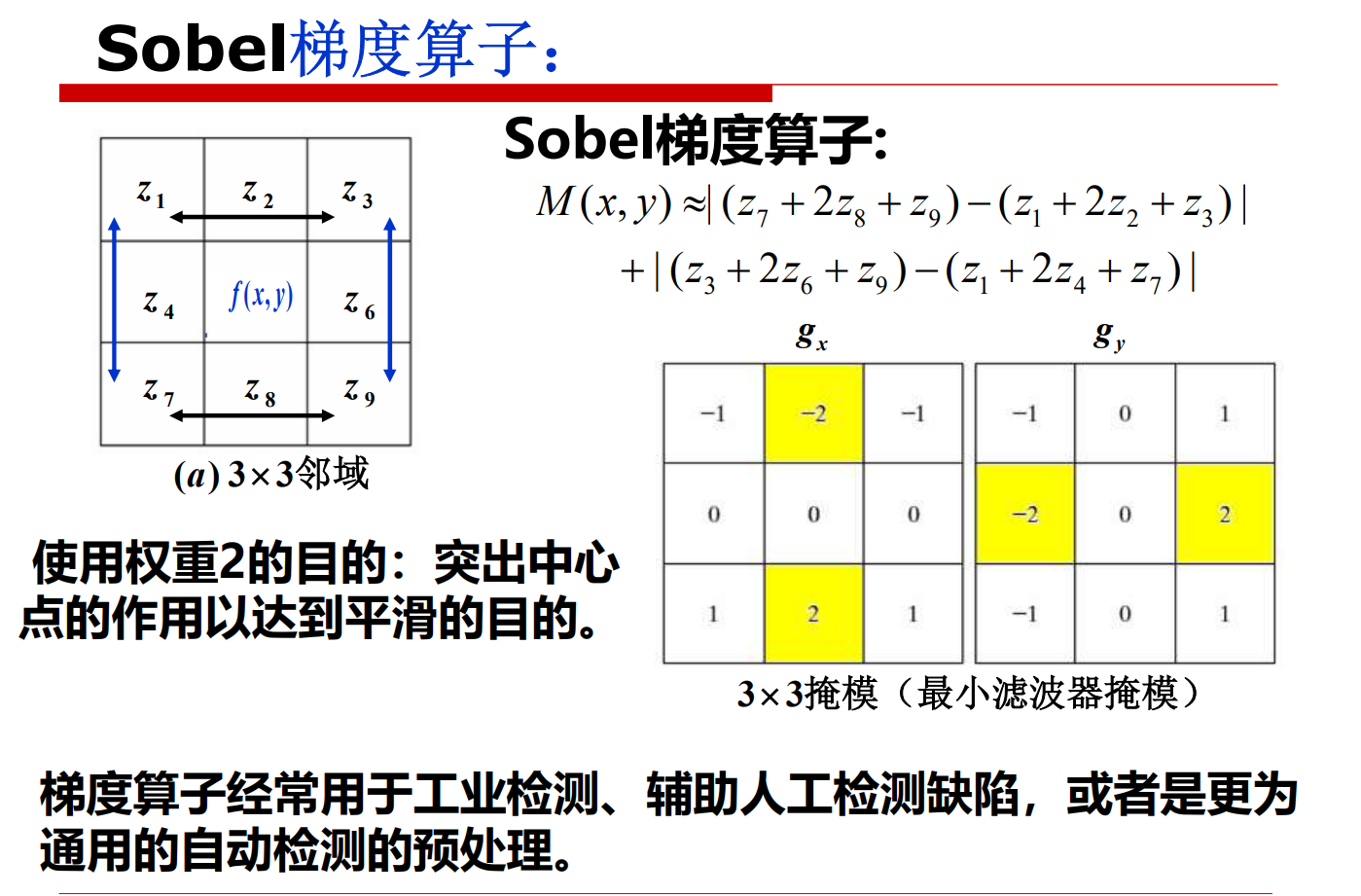
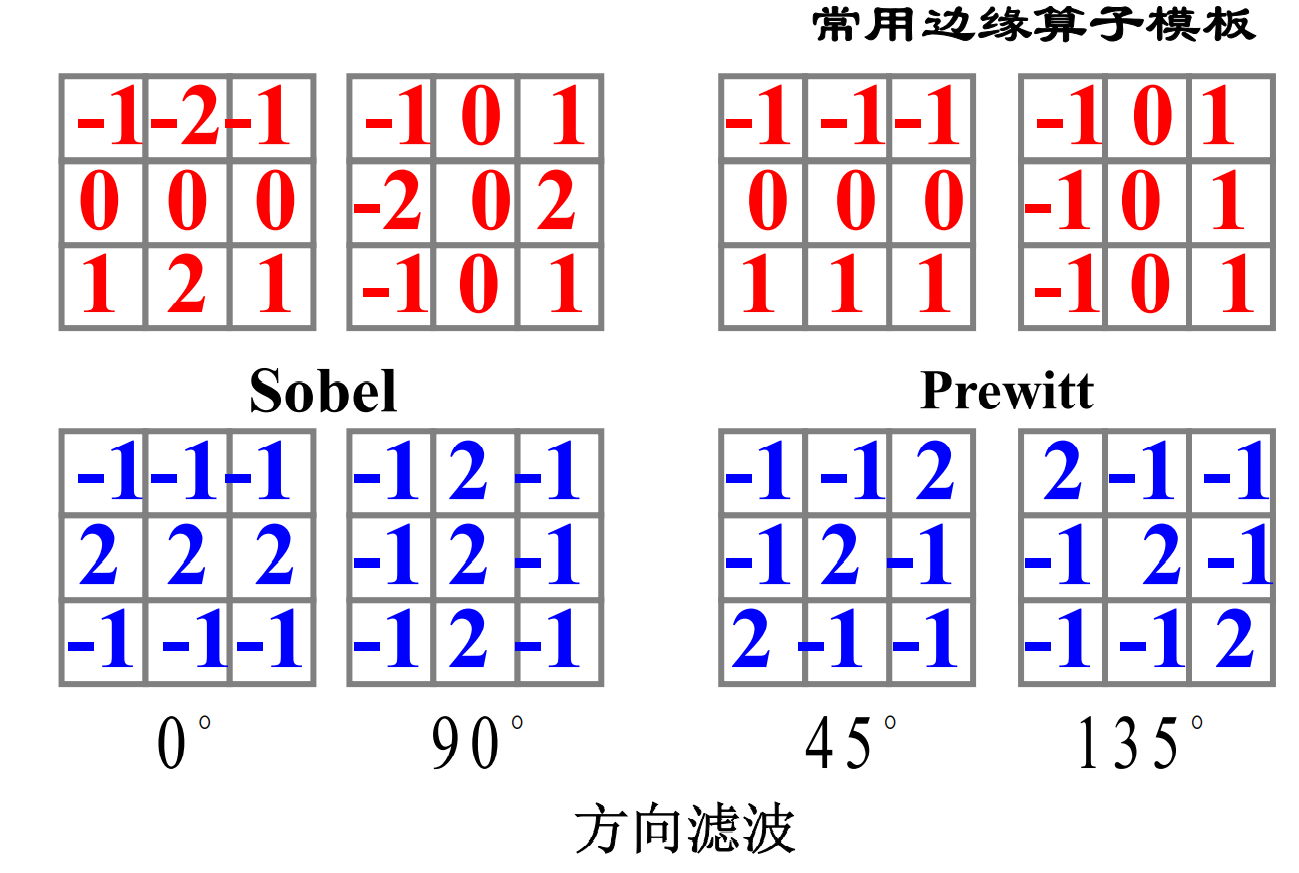
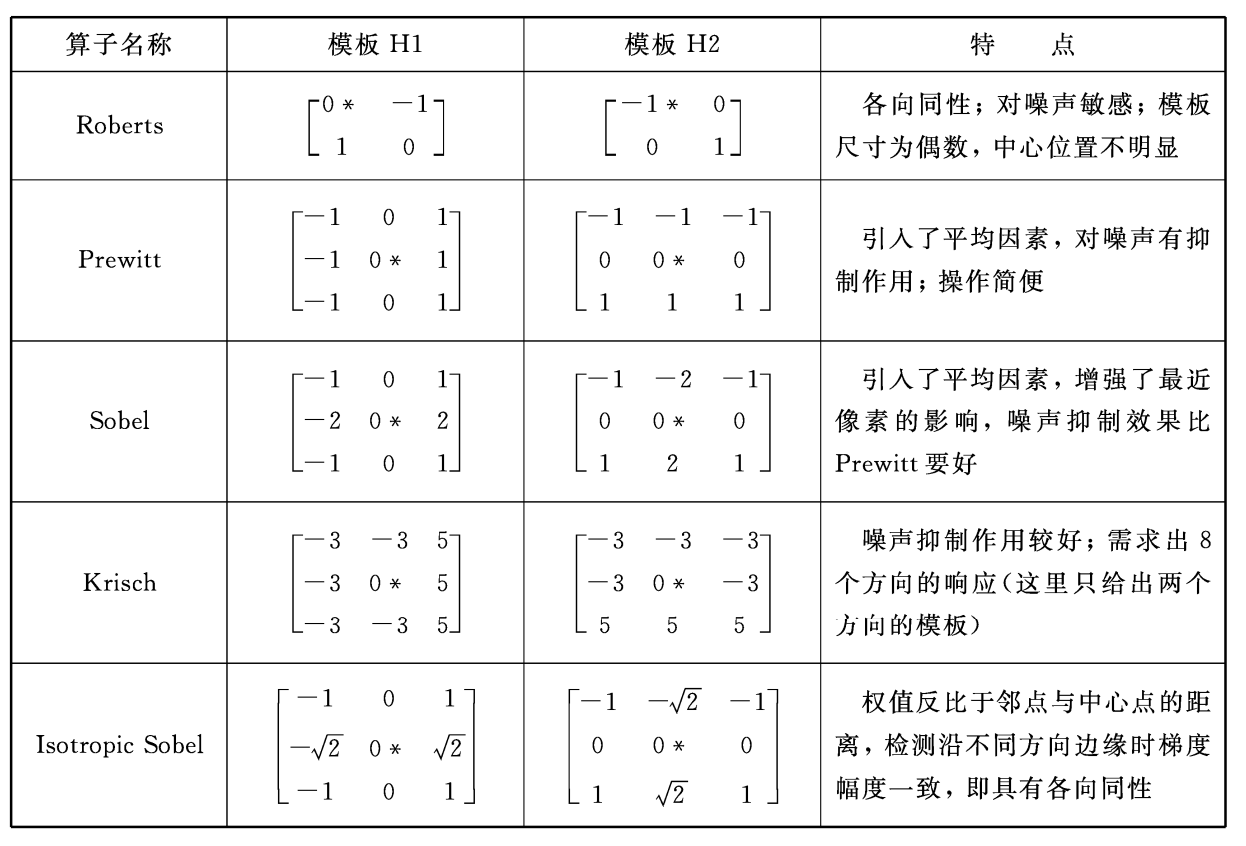
常见的梯度算子
例题
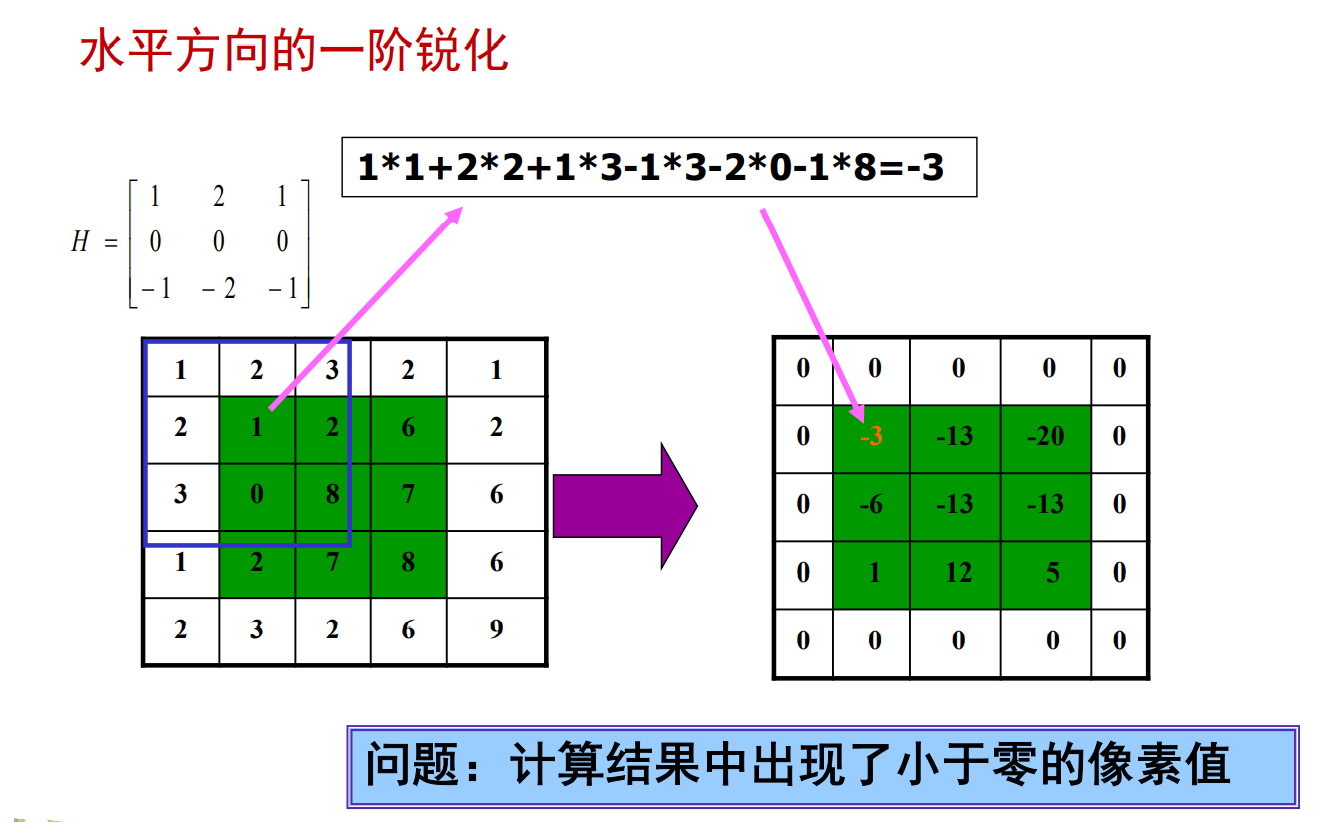
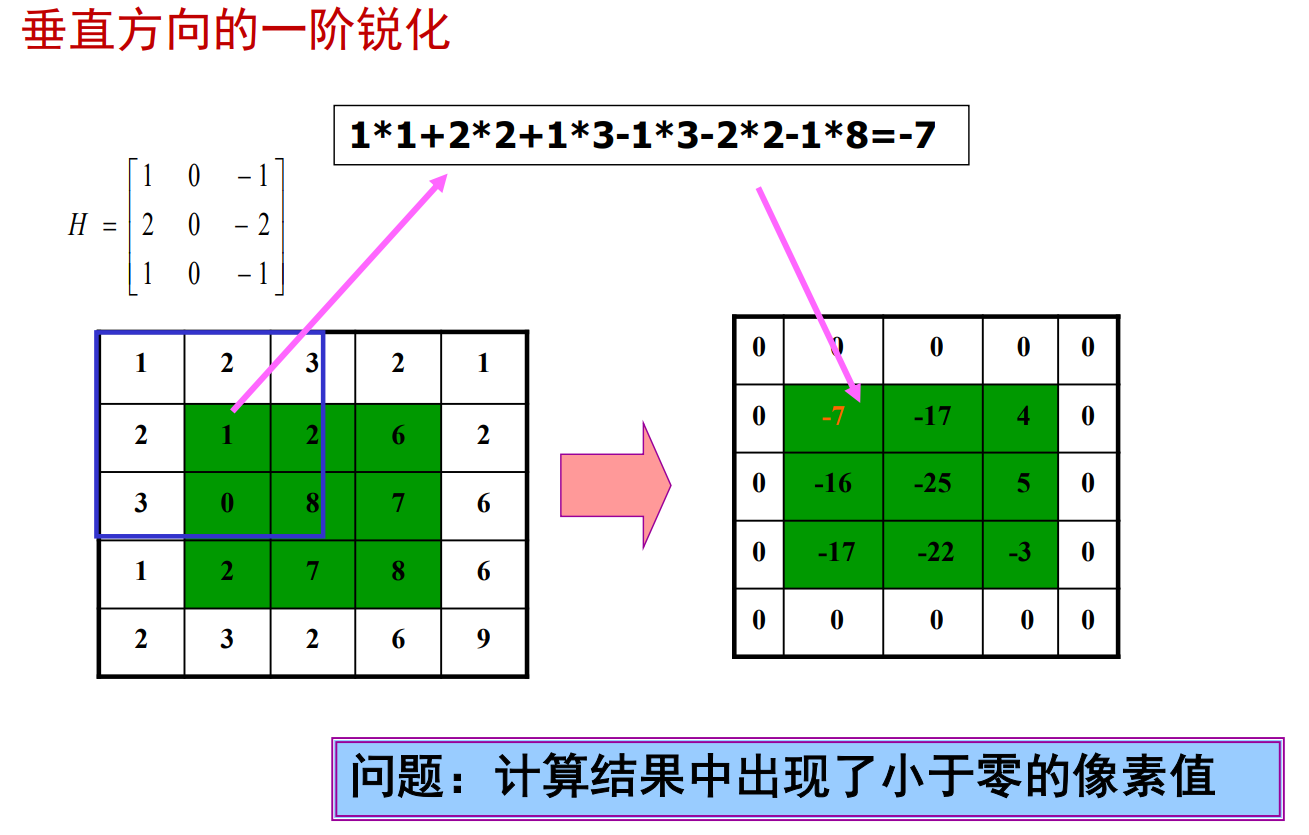
后期处理
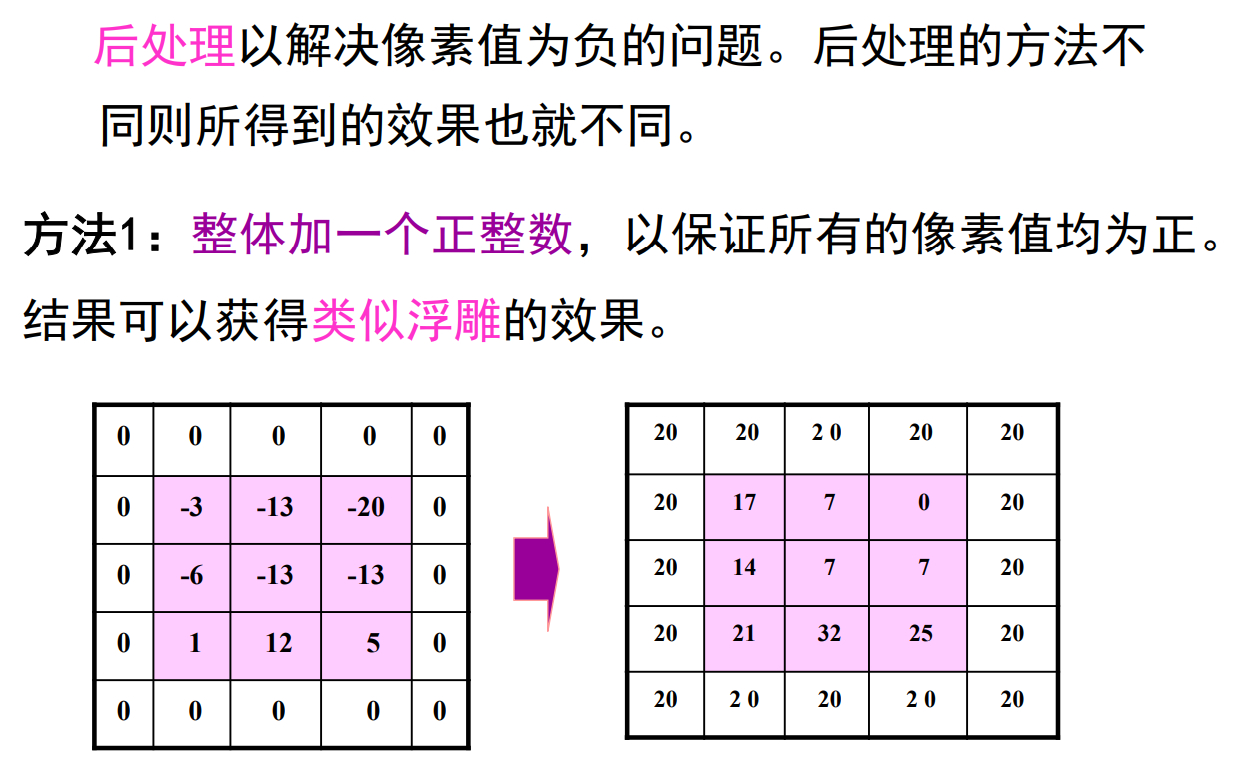
水平浮雕效果

方法2:将所有的像素值取绝对值。可以获得对边缘的有方向提取
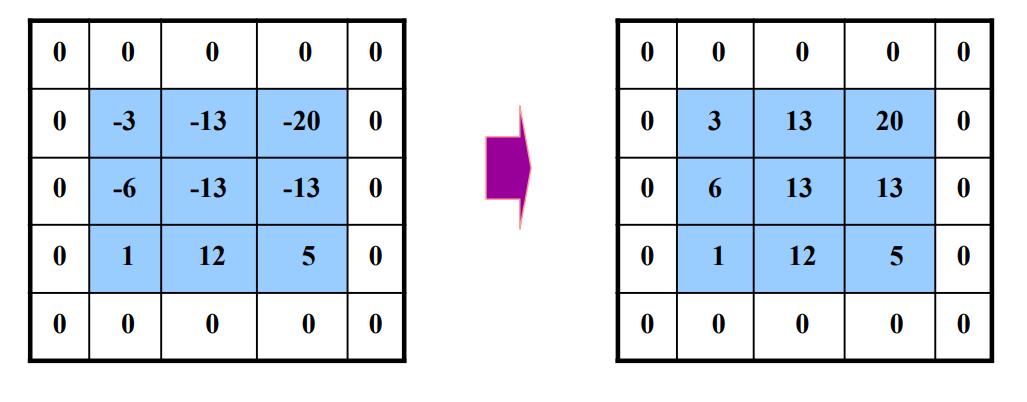
水平边缘的提取效果

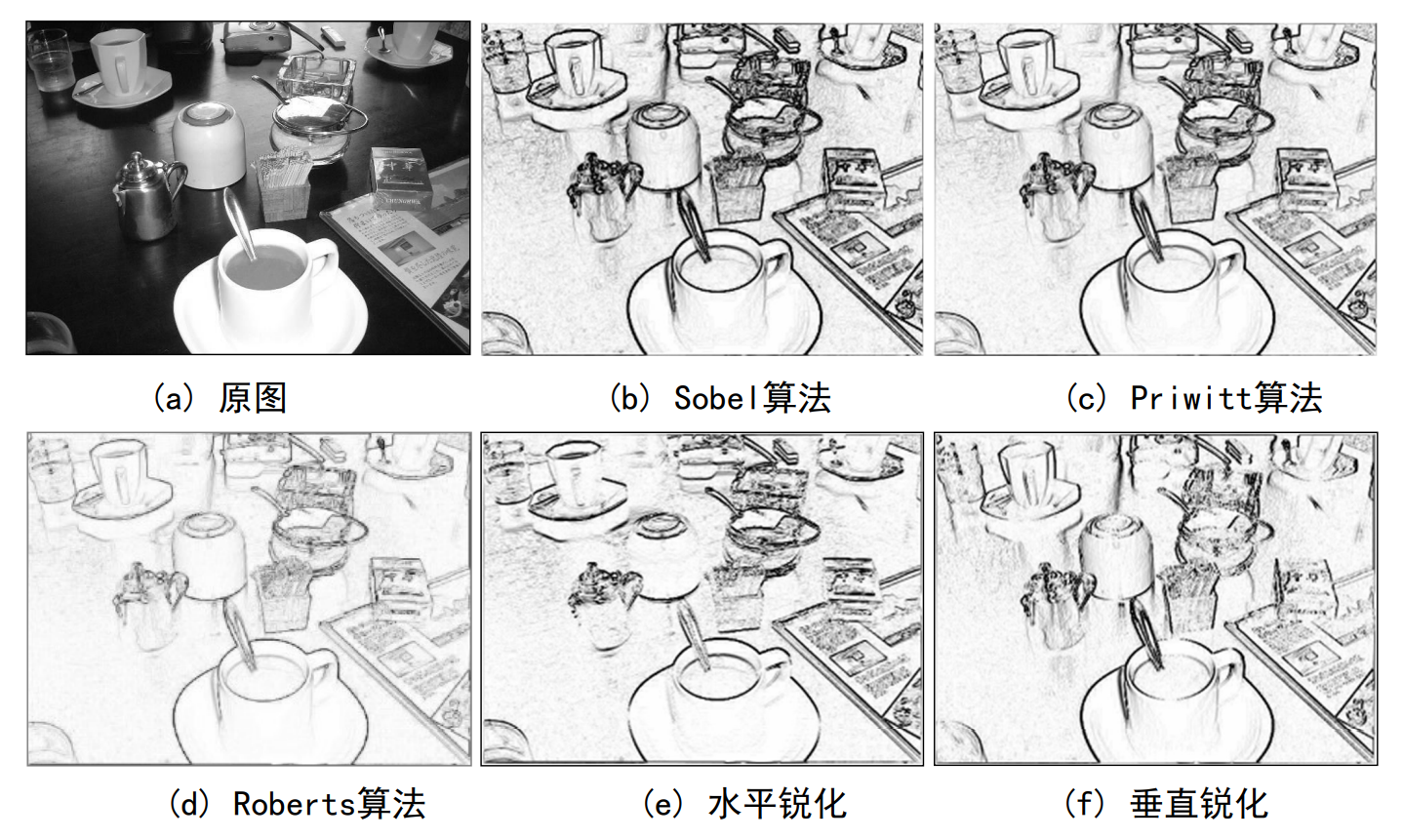
几种一阶锐化方法的效果比较
Sobel算法与Priwitt算法的思路相同,属于同一类型,因此处理效果基本相同。
Roberts算法的模板为2*2,提取出的信息较弱。
方向性锐化经过后处理之后,也可以对边界进行增强。
非锐化滤波
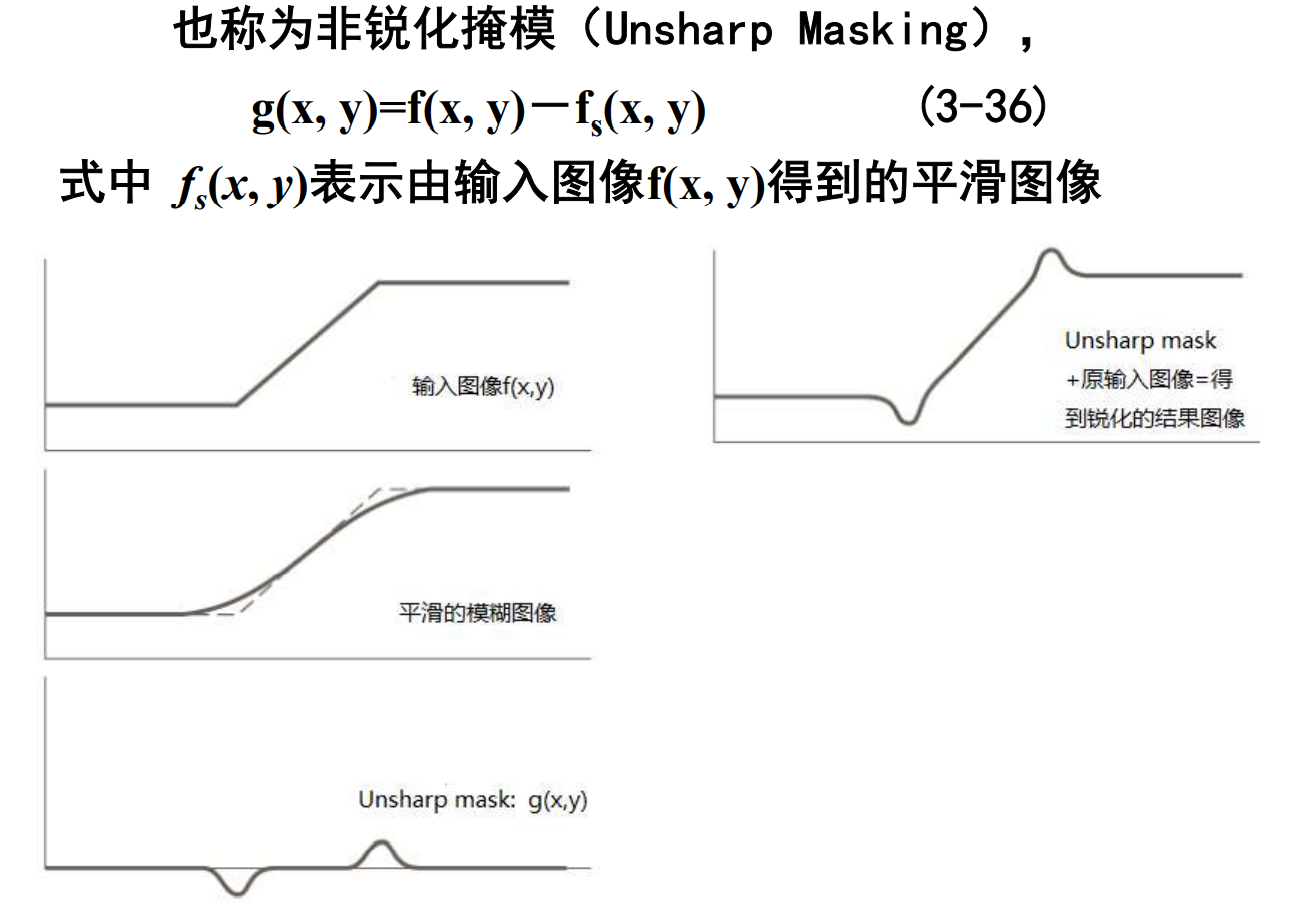
高频增强滤波(highboost filtering)

高频增强滤波示例

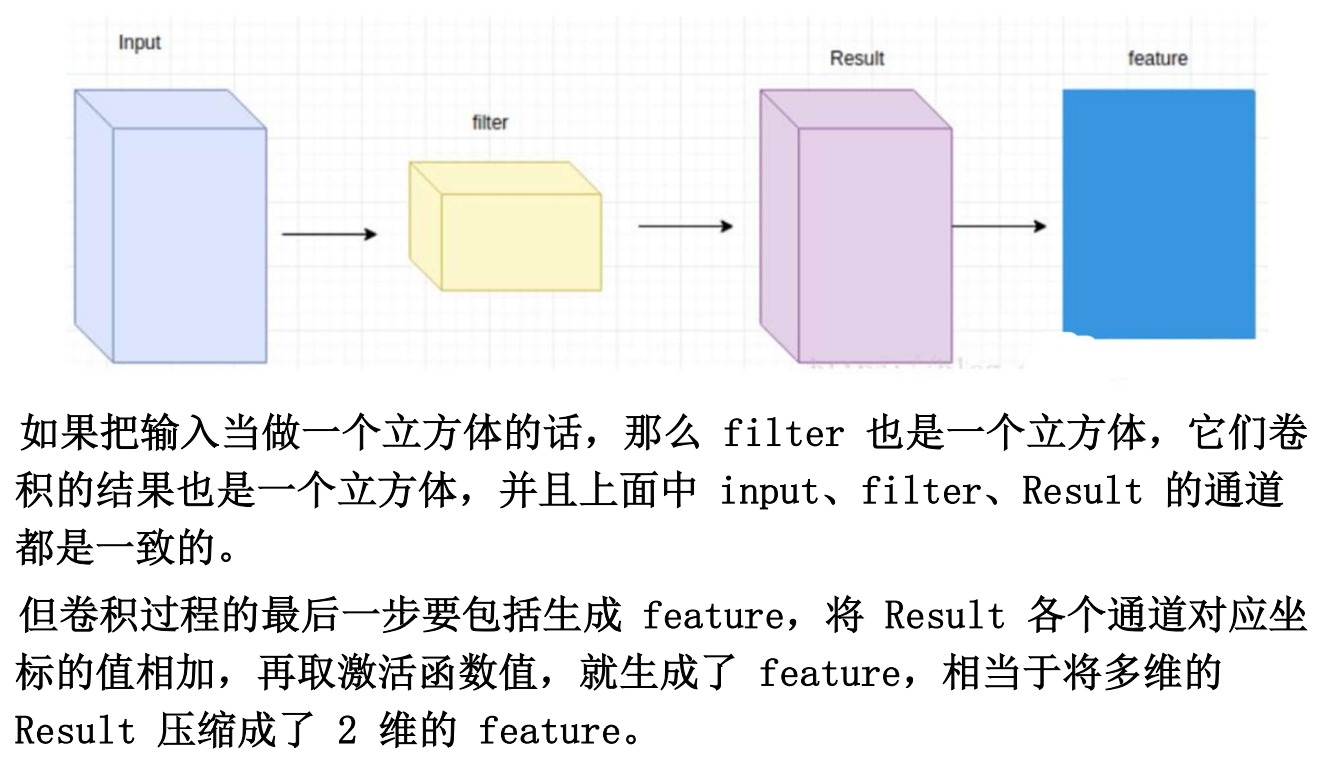
单个卷积核的处理过程