一、评价模型

1.层次分析法（AHP）

层次分析法可以用来进行决策，求指标的权重.

问题的提出：
日常生活中有许多决策问题。决策是指在面临多种方案时需要依据一定的标准选择某一种方案。T.L.Saaty等人在20世纪70年代提出了一种能有效处理决策问题的实用方法，称层次分析法（Analytic Hierarchy Process，简记AHP）

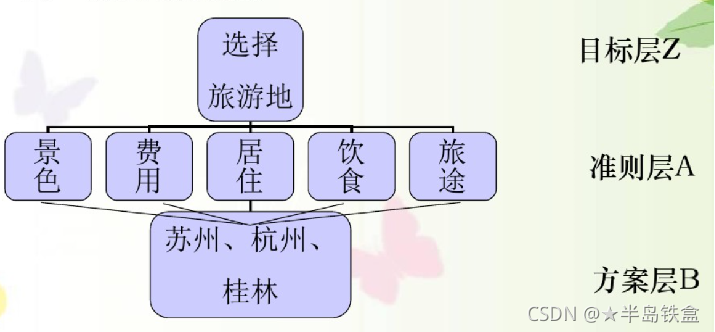
1、首先建立层次结构模型：
一般为三层，最上面的为目标层，最下面的为方案层，中间是准则层或指标层：
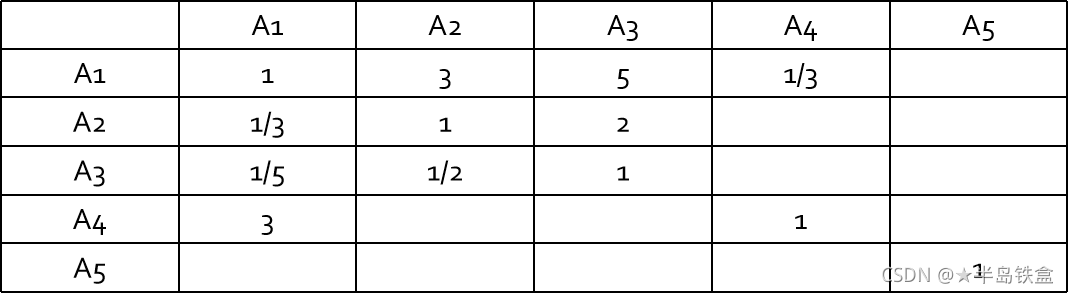
在这里插入图片描述
2、构建成对比较阵：
判断矩阵为两两指标重要性的判断，一般判别矩阵构造如下：

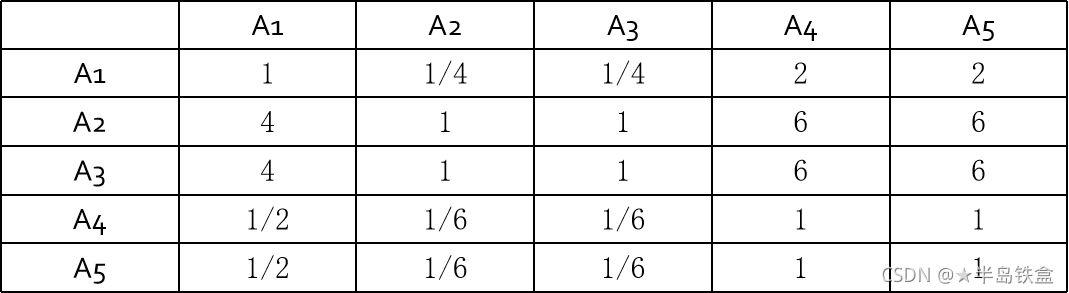
通过上表与各指标关系可以得到如下表的结果：

3、一致性检验（特征根法）
Saaty等人建议用对应于A的最大特征根（记为 λ ）的特征向量（归一化后）作为权向量w，即w满足：
当 λ = n时，该判断矩阵为一致阵，且任何判断矩阵的最大特征根λ≥n
因此，当最大特征根比n大得多时，该判断矩阵的不一致程度越严重。因此可以用 λ-n 的数值大小来衡量判断矩阵的不一致程度，Saaty将：
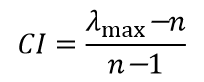
在这里插入图片描述
作为一致性指标，当CI=0时该判断矩阵为一致阵，Saaty又引入了随机一致性指标RI，RI数值如下：

将它的一致性指标CI与同阶（指n相同）的随机一致性指标RI之比称为一致性比率CR，当

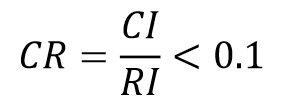
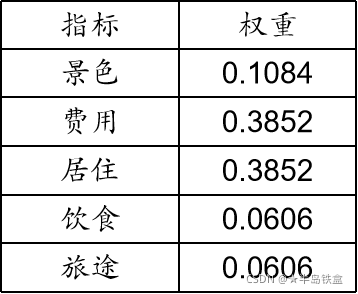
时认为该判断矩阵的不一致程度在容许的范围内，可以用其特征向量作为权向量。最终得到5个指标权重结果
在这里插入图片描述
对上述5个判断矩阵进行计算得到下表：

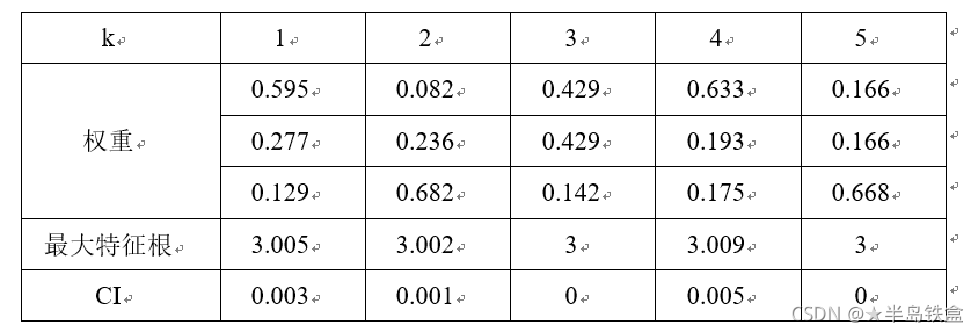
4、计算综合得分：
苏州： 0.10840.595+0.38520.082+0.38520.429+0.06060.633+0.06060.166= 0.3098
杭州： 0.10840.277+0.38520.236+0.38520.429+0.06060.193+0.06060.166= 0.3079
桂林： 0.10840.129+0.38520.682+0.38520.142+0.06060.175+0.0606*0.668= 0.3825

根据综合得分，最终我们选择桂林。

层次分析法（AHP）模型步骤与matlab实现----->见上传资源

2.熵权法

（1）首先对数据进行归一化处理：

由于各项指标计量单位并不统一，因此在计算综合权重前先要对它们进行标准化处理，即把指标的绝对值转化为相对值，并令，从而解决各项不同质指标值的同质化问题。而且，由于正向指标和负向指标数值代表的含义不同（正向指标数值越高越好，负向指标数值越低越好），因此，对于高低指标我们用不同的算法进行数据标准化处理。其具体方法如下:

对于正向指标:
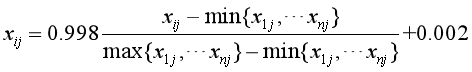
在这里插入图片描述
对于负向指标:

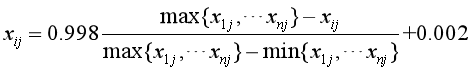
（2）计算第 j 项指标下第 i 方案指标值的比重Pij：

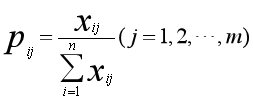
（3）计算第j 项指标的熵值ej：

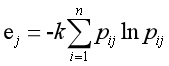
其中

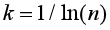
，满足

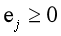
（4）计算信息熵冗余度：

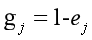
（5）计算各项指标权重

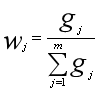
（6）计算综合得分：

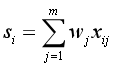
二、预测模型

三、优化模型

1.遗传算法

遗传算法概述：
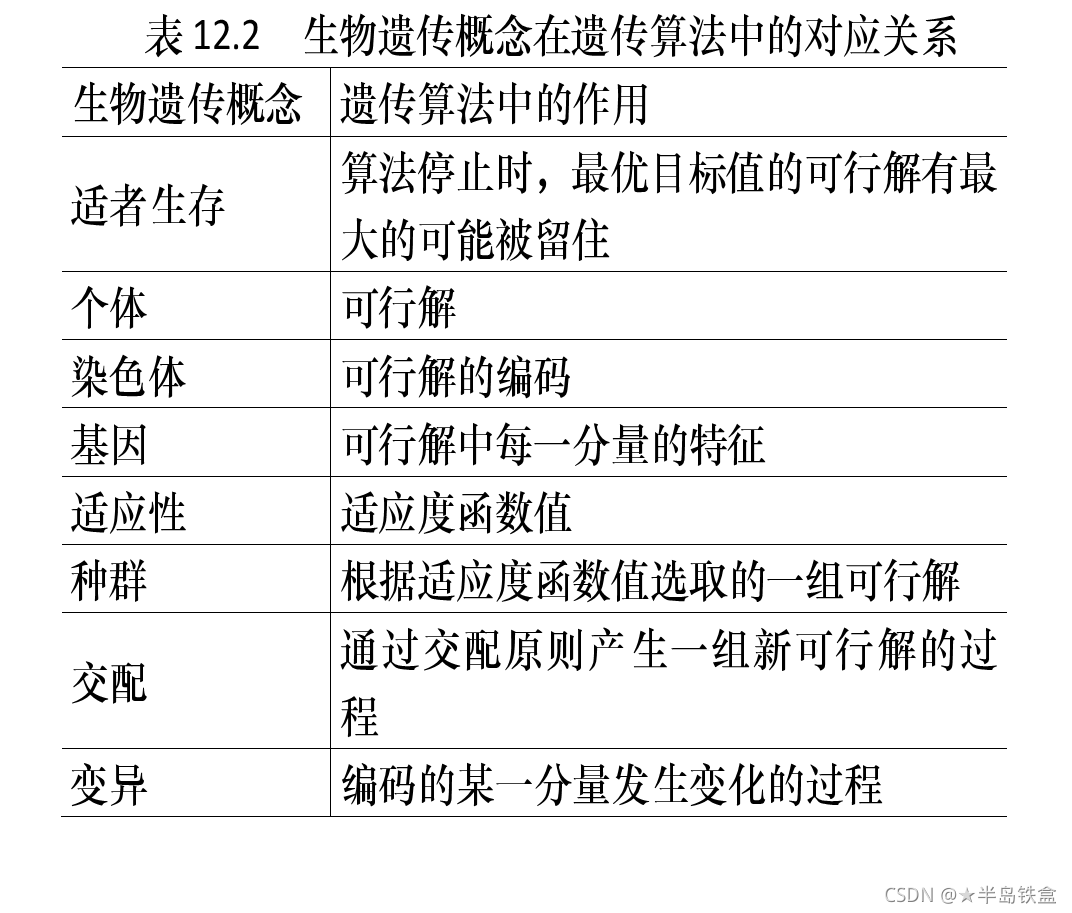
? 遗传算法（Genetic Algorithm，GA）是一种进化算法，其基本原理是仿效生物界中的“物竞天择、适者生存”的演化法，它最初由美国Michigan大学的J. Holland教授于1967年提出。
? 遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。因此，第一步需要实现从表现型到基因型的映射即编码工作。初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择个体，幵借助于自然遗传学的遗传算子（genetic operators）进行组合交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样，后生代种群比前代更加适应于环境，末代种群中的最优个体经过解
码（decoding），可以作为问题近似最优解。

遗传算法有三个基本操作：
选择（Selection）、交叉（Crossover）和变异（Mutation）

? （1）选择。选择的目的是为了从当前群体中选出优良的个体，使它们有机会作为父代为下一代繁衍子孙。根据各个个体的适应度值，按照一定的规则或方法从上一代群体中选择出一些优良的个体遗传到下一代种群中。选择的依据是适应性强的个体为下一代贡献一个或多个后代的概率大。
? （2）交叉。通过交叉操作可以得到新一代个体，新个体组合了父辈个体的特性。将群体中的各个个体随机搭配成对，对每一个个体，以交叉概率交换它们之间的部分染色体。
? （3）变异。对种群中的每一个个体，以变异概率改变某一个或多个基因座上的基因值为其他的等位基因。同生物界中一样，变异发生的概率很低，变异为新个体的产生提供了机会。

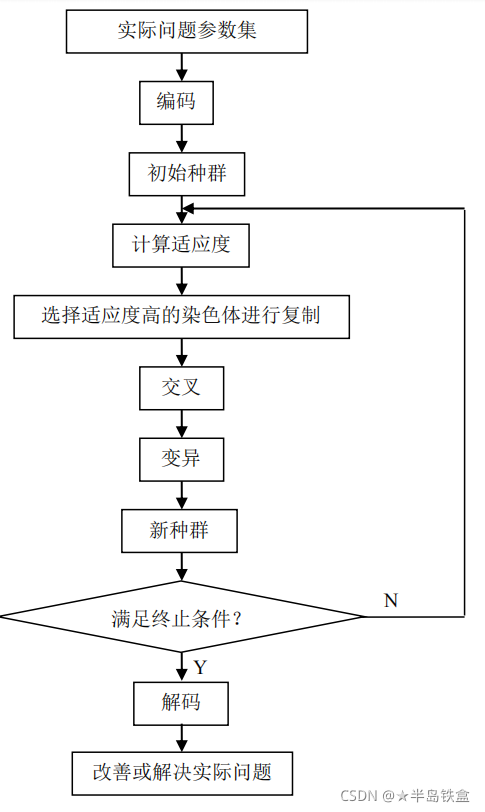
遗传算法的基本步骤：

1)编码：
GA在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据，这些串结构数据的丌同组合便构成了丌同的点。
2)初始群体的生成：
随机产生N个初始串结构数据，每个串结构数据称为一个个体，N个个体构成了一个群体。GA以这N个串结构数据作为初始点开始进化。
3)适应度评估：
适应度表明个体或解的优劣性。丌同的问题，适应性函数的定义方式也不同。
4)选择：
选择的目的是为了从当前群体中选出优良的个体，使它们有机会作为父代为下一代繁殖子孙。遗传算法通过选择过程体现这一思想，进行选择的原则是适应性强的个体为下一代贡献一个或多个后代的概率大。选择体现了达尔文的适者生存原则。
5)交叉：
交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体，新个体组合了其父辈个体的特性。交叉体现了信息交换的思想。
6)变异：
变异首先在群体中随机选择一个个体，对于选中的个体以一定的概率随机地改变串结构数据中某个串的值。同生物界一样， GA中变异发生的概率很低，通常取值很小。
在这里插入图片描述

2.模拟退火算法

模拟退火算法概述
? 模拟退火算法（Simulated Annealing，简称SA）的思想最早是由etropolis等提出的。其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。
模拟退火法是一种通用的优化算法，其物理退火过程由以下三部分组成：
? 加温过程。其目的是增强粒子的热运动，使其偏离平衡位置。当温度足够高时，固体将熔为液体，从而消除系统原先存在的非均匀状态。
? 等温过程。对于与周围环境交换热量而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行的，当自由能达到最小时，系统达到平衡状态。
? 冷却过程。使粒子热运动减弱，系统能量下降，得到晶体结构。
? 加温过程对算法设定初温，等温过程对应算法的Metropolis抽样过程，冷却过程对应控制参数的下降。这里能量的变化就是目标函数，我们要得到的最优解就是能量最低态。其中Metropolis准则是SA算法收敛于全局最优解的关键所在，Metropolis准则以一定的概率接受恶化解，这样就使算法跳离局部最优的陷阱。

模拟退火算法的基本步骤

初始化：取初始温度T0足够大，令T = T0，任取初始解S1。
对当前温度T，重复第（3）～（6）步。
对当前解S1随机扰动产生一个新解S2。
计算S2的增量df = f(S2) - f(S1)，其中f(S1)为S1的代价函数。
若df < 0，则接受S2作为新的当前解，即S1 = S2；否则计算S2的接受概率exp(-df/T)，即随机产生(0,1)区间上均
匀分布的随机数rand，若exp(-df/T) > rand，也接受S2作为新的当前解S1 = S2，否则保留当前解S1。
如果满足终止条件Stop，则输出当前解S1为最优解，结束程序，终止条件Stop通常取为在连续若干个Metropolis
链中新解S2都没有被接受时终止算法或者是设定结束温度；否则按衰减函数衰减T后返回第（2）步。

模拟退火算法的特点
? 与遗传算法等不同，模拟退火算法不需要初始化种群操作。
? 收敛速度较慢。
? 温度管理、退火速度等对寻优结果均有影响。