开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 三维重建工具——pclpy教程之点云features -> 正文阅读

[人工智能]三维重建工具——pclpy教程之点云features

本教程代码开源：GitHub 欢迎star

一、法线估计

1. 参数说明

由于 PCL 中几乎所有类都继承自基本pcl::PCLBase类，因此pcl::Feature类以两种不同的方式接受输入数据：

一个完整的点云数据集，通过setInputCloud (PointCloudConstPtr &) -强制

任何特征估计类都将尝试估计给定输入云中每个点的特征。

点云数据集的子集，通过setInputCloud (PointCloudConstPtr &)和setIndices (IndicesConstPtr &) 给出-可选

任何特征估计类都将尝试估计给定输入云中每个点的特征，该点在给定索引列表中具有索引。默认情况下，如果没有给出一组索引，则将考虑云中的所有点。

此外，可以通过附加调用**setSearchSurface (PointCloudConstPtr &)**指定要使用的点邻居集。此调用是可选的，当未给出搜索面时，默认使用输入点云数据集。

因为**setInputCloud()*总是需要的，所以我们可以使用<setInputCloud(), setIndices(), setSearchSurface()>*创建最多四种组合。假设我们有两个点云，P={p_1, p_2, …p_n} 和 Q={q_1, q_2, …, q_n}。下图显示了所有四种情况：
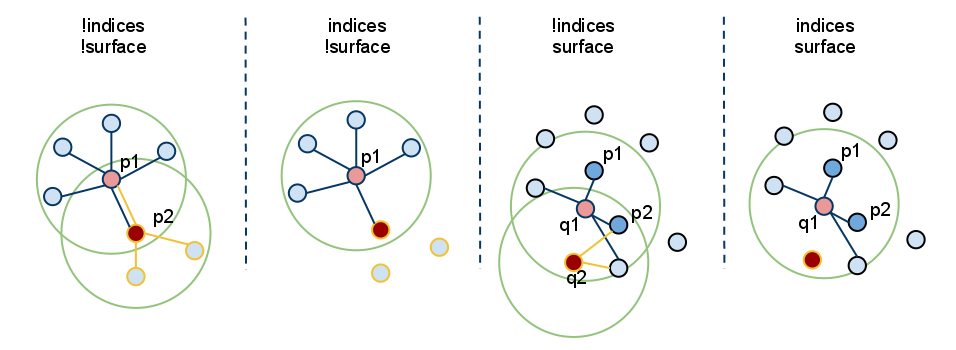
在这里插入图片描述

setIndices() = false, setSearchSurface() = false - 这无疑是 PCL 中最常用的情况，其中用户只是输入单个 PointCloud 数据集并期望在云中的所有点估计某个特征。

由于我们不希望根据是否给出一组索引和/或搜索表面来维护不同的实现副本，因此每当索引 = false 时，PCL 都会创建一组内部索引（作为std::vector）基本上指向整个数据集（索引=1…N，其中 N 是云中的点数）。

在上图中，这对应于最左边的情况。首先，我们估计 p_1 的最近邻居，然后是 p_2 的最近邻居，依此类推，直到我们用尽 P 中的所有点。
setIndices() = true, setSearchSurface() = false - 如前所述，特征估计方法只会计算那些在给定索引向量中有索引的点的特征；

在上图中，这对应于第二种情况。在这里，我们假设 p_2 的索引不是给定的索引向量的一部分，因此不会在 p2 估计邻居或特征。
setIndices() = false, setSearchSurface() = true - 与第一种情况一样，将对作为输入给出的所有点的特征进行估计，但是，在setSearchSurface() 中给出的底层相邻表面将用于获取输入的最近邻点，而不是输入云本身；

在上图中，这对应于第三种情况。如果 Q={q_1, q_2} 是另一个作为输入给出的云，不同于 P，并且 P 是 Q 的搜索表面，那么 q_1 和 q_2 的邻居将从 P 计算。
setIndices() = true, setSearchSurface() = true - 这可能是最罕见的情况，其中索引和搜索表面都被给出。在这种情况下，将使用setSearchSurface() 中给出的搜索表面信息，仅为<input,indices> 对中的一个子集估计特征。

最后，在上图中，这对应于最后一个（最右边）的情况。在这里，我们假设 q_2 的索引不是为 Q 给出的索引向量的一部分，因此不会在 q2 估计邻居或特征。

应该使用**setSearchSurface()**时最有用的例子是，当我们有一个非常密集的输入数据集，但我们不想估计其中所有点的特征，而是估计使用pcl_keypoints 中的方法发现的某些关键点=时，或者在云的下采样版本（例如，使用pcl::VoxelGrid过滤器获得）。在这种情况下，我们通过setInputCloud()传递下采样/关键点输入，并将原始数据作为setSearchSurface() 传递。

2. 例子

输入一旦确定，就可使用查询点的相邻点来估计局部特征表示，这表示捕获查询点周围的底层采样表面的几何形状。描述表面几何形状的一个重要问题是首先推断其在坐标系中的方向，即估计其法线。表面法线是表面的重要属性，在许多领域（例如计算机图形应用程序）中大量使用，以应用生成阴影和其他视觉效果的正确光源（有关更多信息，请参阅[RusuDissertation]）。
代码见01_3DFeaturesWork.py

为输入数据集中的所有点估计一组表面法线

# 估计法线
# 输入数据集中的所有点估计一组表面法线
ne = pcl.features.NormalEstimation.PointXYZ_Normal()
ne.setInputCloud(cloud)
tree = pcl.search.KdTree.PointXYZ()
ne.setSearchMethod(tree)

cloud_normals = pcl.PointCloud.Normal()
ne.setRadiusSearch(0.003)
ne.compute(cloud_normals)
print(cloud_normals.size())

为输入数据集中的点子集估计一组表面法线。

ne = pcl.features.NormalEstimation.PointXYZ_Normal()
ne.setInputCloud(cloud)
tree = pcl.search.KdTree.PointXYZ()
ne.setSearchMethod(tree)
ind = pcl.PointIndices()
[ind.indices.append(i) for i in range(0, cloud.size() // 2)]
ne.setIndices(ind)
cloud_normals = pcl.PointCloud.Normal()
ne.setRadiusSearch(0.003)
ne.compute(cloud_normals)
print(cloud_normals.size())

为输入数据集中的所有点估计一组表面法线，但使用另一个数据集估计它们的最近邻

在这里，我们使用点云的下采样点云作为输入点云，使用原点云作为SearchSurface。

ne = pcl.features.NormalEstimation.PointXYZ_Normal()
cloud_downsampled = pcl.PointCloud.PointXYZ()  # 获取一个降采样的点云 方法比较多，这里使用voxelized方法
vox = pcl.filters.VoxelGrid.PointXYZ()
vox.setInputCloud(cloud)
vox.setLeafSize(0.005, 0.005, 0.005)
vox.filter(cloud_downsampled)
ne.setInputCloud(cloud_downsampled)
ne.setSearchSurface(cloud)
tree = pcl.search.KdTree.PointXYZ()
ne.setSearchMethod(tree)
cloud_normals = pcl.PointCloud.Normal()
ne.setRadiusSearch(0.003)
ne.compute(cloud_normals)
print(cloud_normals.size())

下图分别为原始电云和下采样点云。
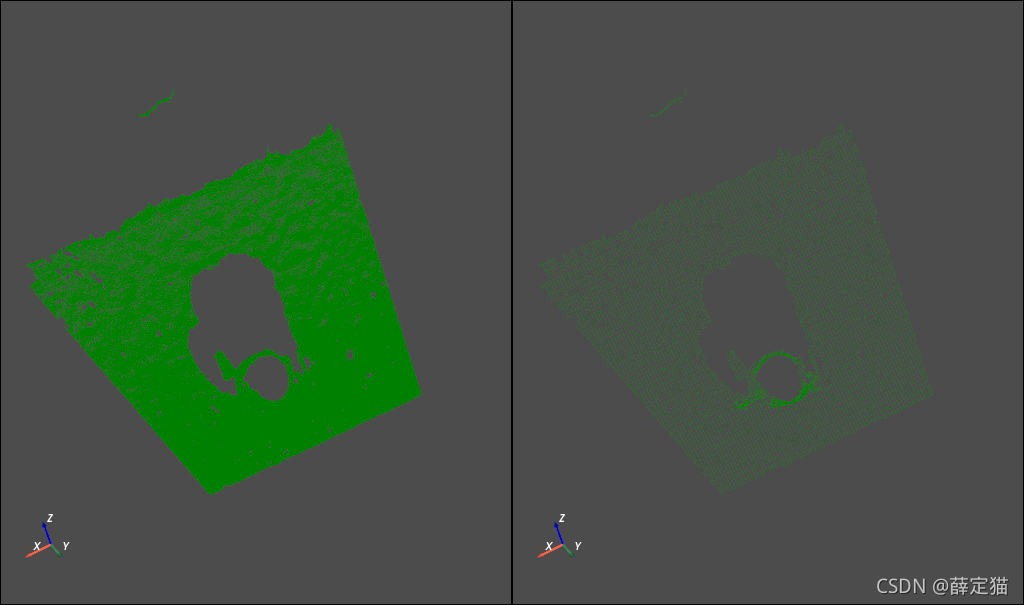
在这里插入图片描述

详细内容可参考how-3d-features-work，本文档不再赘述。

二、使用积分图像的法线估计

在本教程中，我们将学习如何使用积分图像计算有组织的点云的法线。

1. 代码

见04_normal_estimation_using_integral_images.py

# 加载点云
cloud = pcl.PointCloud.PointXYZ()
reader = pcl.io.PCDReader()
reader.read("../../data/table_scene_mug_stereo_textured.pcd", cloud)
# 估计法线
normals = pcl.PointCloud.Normal()
ne = pcl.features.IntegralImageNormalEstimation.PointXYZ_Normal()
ne.setNormalEstimationMethod(ne.AVERAGE_3D_GRADIENT)
ne.setMaxDepthChangeFactor(0.02)
ne.setNormalSmoothingSize(10.0)
ne.setInputCloud(cloud)
ne.compute(normals)

# # 可视化
# viewer = pcl.visualization.PCLVisualizer("viewer")
# viewer.setBackgroundColor(0.0, 0.0, 0.0)
# viewer.addPointCloud(cloud, "sample cloud")  # 显示点云
# # viewer.addPointCloudNormals(cloud, normals)  # 显示点云和法线 该函数bug未修复~
#
# while not viewer.wasStopped():
#     viewer.spinOnce(10)

# 使用pyvista可视化
p = pv.Plotter()
cloud = pv.wrap(cloud.xyz)
p.add_mesh(cloud, point_size=1, color='g')
p.camera_position = 'iso'
p.enable_parallel_projection()
p.show_axes()
p.show()

在可视化法线时，遇到了一下错误：

In..\Rendering\Core\vtkActor.cxx, line 43. Error: no override found for vtkactor

查看了pclpy的官方Issue，发现有人提过这个Issue，这个bug还未修复

issue:https://github.com/davidcaron/pclpy/issues/58

感觉pclpy在可视化这一块儿bug比较多（目前已发现的有：无法可视化mesh、带法线的点云），在python中可视化功能可使用pyvista代替。事实上，作者可能也意识到了这个问题，在最新的pclpy v1.12.0移除了可视化模块。

2. 说明

这里只挑重要的几行代码说一下。

# 估计法线
normals = pcl.PointCloud.Normal()
ne = pcl.features.IntegralImageNormalEstimation.PointXYZ_Normal()
ne.setNormalEstimationMethod(ne.AVERAGE_3D_GRADIENT)
ne.setMaxDepthChangeFactor(0.02)
ne.setNormalSmoothingSize(10.0)
ne.setInputCloud(cloud)
ne.compute(normals)

可以使用以下常规估计方法：

enum NormalEstimationMethod
{
  COVARIANCE_MATRIX,
  AVERAGE_3D_GRADIENT,
  AVERAGE_DEPTH_CHANGE
};

COVARIANCE_MATRIX 模式创建 9 个积分图像，以根据其局部邻域的协方差矩阵计算特定点的法线。AVERAGE_3D_GRADIENT 模式创建 6 个积分图像来计算水平和垂直 3D 梯度的平滑版本，并使用这两个梯度之间的叉积计算法线。AVERAGE_DEPTH_CHANGE 模式仅创建单个积分图像并根据平均深度变化计算法线。

参考：Normal Estimation Using Integral Images

三、点特征直方图（PFH）

理论部分请参考RusuDissertation 。在此不再赘述。

1. 代码

点特征直方图作为pcl_features库的一部分在 PCL 中实现。

默认的 PFH 实现使用 5 个分箱细分（例如，四个特征值中的每一个都将使用其值区间中的这么多分箱），并且不包括距离（如上所述 - 尽管如果需要，用户可以调用computePairFeatures方法来获取距离），这会生成一个 125 字节 $5^3$ 的浮点值数组 ( )。这些存储在pcl::PFHSignature125点类型中。

以下代码片段将为输入数据集中的所有点估计一组 PFH 特征。
见05_PHF_descriptors.py

import pclpy
from pclpy import pcl
import numpy as np
import sys

if __name__ == '__main__':
    # 生成点云数据
    # 加载点云
    cloud = pcl.PointCloud.PointXYZ()
    reader = pcl.io.PCDReader()
    reader.read("../../data/bunny.pcd", cloud)
    print(cloud.size())
    # 构造法线估计类
    ne = pcl.features.NormalEstimation.PointXYZ_Normal()
    ne.setInputCloud(cloud)

    tree = pcl.search.KdTree.PointXYZ()
    ne.setSearchMethod(tree)

    normals = pcl.PointCloud.Normal()
    ne.setRadiusSearch(0.03)
    # 计算法线
    ne.compute(normals)
    print(normals.size())

    # 构造PFH estimation类，把cloud和normals传递进去
    pfh = pcl.features.PFHEstimation.PointXYZ_Normal_PFHSignature125()
    pfh.setInputCloud(cloud)
    pfh.setInputNormals(normals)
    # 或者，如果cloud是PointNormal类型，执行pfh.setInputNormals(cloud);

    # 构造一个kd树
    # 它的内容将根据给定的输入点云填充到对象内部(因为没有给出其他搜索面)。
    tree = pcl.search.KdTree.PointXYZ()
    pfh.setSearchMethod(tree)

    # 输出
    pfhs = pcl.PointCloud.PFHSignature125()

    # 使用5cmm球形范围内的邻居点
    # 注意：在这里使用的半径必须大于用来估计表面法线的半径!!
    pfh.setRadiusSearch(0.05)

    # 计算特征
    pfh.compute(pfhs)

    print(pfhs.size())  # pfhs与cloud size应该相同

来自PFHEstimation类的实际计算调用在内部不执行任何操作，但它做了下面的事：

for each point p in cloud P
  1. get the nearest neighbors of p
  2. for each pair of neighbors, compute the three angular values
  3. bin all the results in an output histogram

要从 k 邻域计算单个 PFH 表示，PCL 可以使用：

computePointPFHSignature (const pcl::PointCloud<PointInT> &cloud,
                          const pcl::PointCloud<PointNT> &normals,
                          const std::vector<int> &indices,
                          int nr_split,
                          Eigen::VectorXf &pfh_histogram);

但是pclpy尚未实现该函数。

出于效率原因，PFHEstimation中的计算方法不检查法线是否包含 NaN 或无限值。将这些值传递给**compute()将导致未定义的输出。建议至少在设计处理链或设置参数时检查法线。这可以通过在调用compute()**之前插入以下代码来完成：
for i in range(normals.size()):
 if not pcl.common.isFinite(normals.at(i)):
     print('normals[%d] is not finite\n', i)
在生产代码中，应设置预处理步骤和参数，以便法线有限否则会引发错误。

经过测试，pclpy的isFinite()函数似乎不支持pcl.PointCloud.Normal()类型的点，emmmmm，pclpy的bug还是有点多啊

参考：https://pcl.readthedocs.io/projects/tutorials/en/latest/pfh_estimation.html#pfh-estimation

四、快速点特征直方图（FPFH）描述符

理论部分请参考：RusuDissertation，在此不再赘述。

1. PFH 和 FPFH 之间的差异

PFH 和 FPFH 配方之间的主要区别总结如下：

$p_q$ 从图中可以看出，FPFH 并没有完全互连的所有邻居，因此缺少一些可能有助于捕获查询点周围几何的值对；
PFH 对查询点周围的精确确定的表面进行建模，而 FPFH 包括r半径球体之外的附加点对（尽管最多2r远）；
由于重新加权方案，FPFH结合了SPFH值并重新捕获了一些点相邻值对；
FPFH的整体复杂度大大降低，从而使其在实时应用中使用成为可能；
结果直方图通过去相关值来简化，即简单地创建d 个单独的特征直方图，每个特征维度一个，并将它们连接在一起（见下图）。

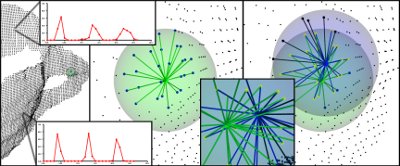
在这里插入图片描述

2. 代码

默认的 FPFH 实现使用 11 个分箱细分（例如，四个特征值中的每一个都将使用来自其值区间的这么多分箱）和去相关方案（见上文：特征直方图单独计算并合并），结果为 33 -byte 浮点值数组。这些存储在pcl::FPFHSignature33点类型中。

以下代码片段将为输入数据集中的所有点估计一组 FPFH 特征。
见06_FPFH_descriptors.py

import pclpy
from pclpy import pcl
import numpy as np
import sys

if __name__ == '__main__':
    # 生成点云数据
    # 加载点云
    cloud = pcl.PointCloud.PointXYZ()
    reader = pcl.io.PCDReader()
    reader.read("../../data/bunny.pcd", cloud)
    print(cloud.size())
    # 构造法线估计类
    ne = pcl.features.NormalEstimation.PointXYZ_Normal()
    ne.setInputCloud(cloud)

    tree = pcl.search.KdTree.PointXYZ()
    ne.setSearchMethod(tree)

    normals = pcl.PointCloud.Normal()
    ne.setRadiusSearch(0.03)
    # 计算法线
    ne.compute(normals)
    print(normals.size())
    
    # 构造FPFH estimation类，把cloud和normals传递进去
    fpfh = pcl.features.FPFHEstimation.PointXYZ_Normal_FPFHSignature33()
    fpfh.setInputCloud(cloud)
    fpfh.setInputNormals(normals)
    # 或者，如果cloud是PointNormal类型，执行fpfh.setInputNormals(cloud);

    # 构造一个kd树
    # 它的内容将根据给定的输入点云填充到对象内部(因为没有给出其他搜索面)。
    tree = pcl.search.KdTree.PointXYZ()
    fpfh.setSearchMethod(tree)

    # 输出
    pfhs = pcl.PointCloud.FPFHSignature33()

    # 使用5cmm球形范围内的邻居点
    # 注意：在这里使用的半径必须大于用来估计表面法线的半径!!
    fpfh.setRadiusSearch(0.05)

    # 计算特征
    fpfh.compute(pfhs)
    print(pfhs.size())  # pfhs与cloud size应该相同

来自FPFHEstimation类的实际计算调用在内部不执行任何操作，但做了下面的事情：

for each point p in cloud P
  1. pass 1:
     1. get the nearest neighbors of :math:`p`
     2. for each pair of :math:`p, p_i` (where :math:`p_i` is a neighbor of :math:`p`, compute the three angular values
     3. bin all the results in an output SPFH histogram
  2. pass 2:
     1. get the nearest neighbors of :math:`p`
     3. use each SPFH of :math:`p` with a weighting scheme to assemble the FPFH of :math:`p`:

同样的，出于效率原因，FPFHEstimation中的计算方法不检查法线是否包含 NaN 或无限值。将这些值传递给**compute()将导致未定义的输出。建议至少在设计处理链或设置参数时检查法线。这可以通过在调用compute()**之前插入以下代码来完成：
for i in range(normals.size()):
 if not pcl.common.isFinite(normals.at(i)):
     print('normals[%d] is not finite\n', i)
在生产代码中，应设置预处理步骤和参数，以便法线有限否则会引发错误。

经过测试，pclpy的isFinite()函数似乎不支持pcl.PointCloud.Normal()类型的点，emmmmm，pclpy的bug还是有点多啊

五、估计一组点的VFH特征

理论部分请参阅：使用 VFH 描述符和/或[VFH] 的集群识别和 6DOF 姿态估计在此不再赘述。

1. 代码

视点特征直方图作为pcl_features 库的一部分在 PCL 中实现。

默认的 VFH 实现对三个扩展的 FPFH 值中的每一个使用 45 个分箱细分，再加上每个点和质心之间的距离的另外 45 个分箱细分和视点组件的 128 个分箱细分，从而产生一个 308 字节的浮点数组值。它们存储在pcl::VFHSignature308点类型中。

PFH/FPFH 描述符和 VFH 之间的主要区别在于，对于给定的点云数据集，只会估计单个 VFH 描述符，而生成的 PFH/FPFH 数据将具有与点数相同的条目数云端。

以下代码片段将为输入数据集中的所有点估计一组 VFH 特征。

见07_VFH_descriptors.py

cloud = pcl.PointCloud.PointXYZ()
reader = pcl.io.PCDReader()
reader.read("../../data/bunny.pcd", cloud)
print(cloud.size())
# 构造法线估计类
ne = pcl.features.NormalEstimation.PointXYZ_Normal()
ne.setInputCloud(cloud)

tree = pcl.search.KdTree.PointXYZ()
ne.setSearchMethod(tree)

normals = pcl.PointCloud.Normal()
ne.setRadiusSearch(0.03)
# 计算法线
ne.compute(normals)
print(normals.size())

cloud_normals = pcl.PointCloud.PointNormal().from_array(
    np.hstack((cloud.xyz, normals.normals, normals.curvature.reshape(-1, 1))))
for i in range(cloud_normals.size()):
    if not pcl.common.isFinite(cloud_normals.at(i)):
        print('cloud_normals[%d] is not finite\n', i)

        # 构造VFH estimation类，把cloud和normals传递进去
        vfh = pcl.features.VFHEstimation.PointXYZ_Normal_VFHSignature308()
        vfh.setInputCloud(cloud)
        vfh.setInputNormals(normals)
        # 或者，如果cloud是PointNormal类型，执行vfh.setInputNormals(cloud);

        # 构造一个kd树
        # 它的内容将根据给定的输入点云填充到对象内部(因为没有给出其他搜索面)。
        tree = pcl.search.KdTree.PointXYZ()
        vfh.setSearchMethod(tree)

        # 输出
        vfhs = pcl.PointCloud.VFHSignature308()

        # 计算特征
        vfh.compute(vfhs)

        print(vfhs.size())  # pfhs的size应该为1

2. 可视化VFH特征

PCL里面可以使用PCLHistogramVisualization类来可视化，python环境下选择就比较多了，下面使用Matplotlib来进行绘制。

# 使用matplotlib绘制直方图
plt.plot(vfhs.histogram[0])
plt.show()

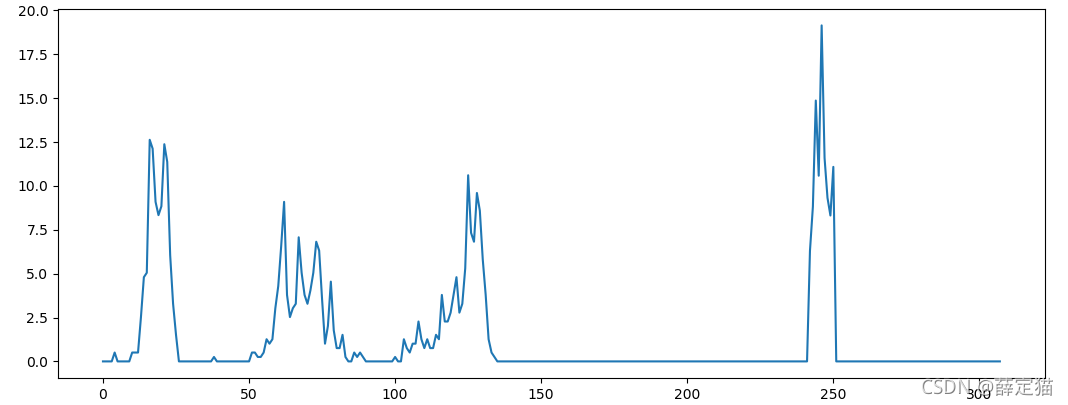
在这里插入图片描述

参考： ( 1 , 2 ) http://www.willowgarage.com/sites/default/files/Rusu10IROS.pdf

六、基于转动惯量和偏心率的描述符（存在bug）

在本教程中，我们将学习如何使用pcl::MomentOfInertiaEstimation类来获取基于偏心率和转动惯量的描述符。此类还允许提取云的轴对齐和定向边界框。但请记住，提取的 OBB 不是最小可能的边界框。

理论部分请参考：Moment of inertia and eccentricity based descriptors
或访问基于转动惯量和偏心率的描述符

1. 代码

本教程点云文件： here

见08_moment_of_inertia.py

# 加载点云
cloud = pcl.PointCloud.PointXYZ()
reader = pcl.io.PCDReader()
reader.read("../../data/min_cut_segmentation_tutorial.pcd", cloud)

print(cloud.size())

feature_extractor = pcl.features.MomentOfInertiaEstimation.PointXYZ()
feature_extractor.setInputCloud(cloud)
feature_extractor.compute()

moment_of_inertia = pcl.vectors.Float()
eccentricity = pcl.vectors.Float()

min_point_AABB = pcl.point_types.PointXYZ()
max_point_AABB = pcl.point_types.PointXYZ()
min_point_OBB = pcl.point_types.PointXYZ()
max_point_OBB = pcl.point_types.PointXYZ()
position_OBB = pcl.point_types.PointXYZ()

rotational_matrix_OBB = np.zeros((3, 3), np.float)
major_value, middle_value, minor_value = 0.0, 0.0, 0.0
major_vector = np.zeros((3, 1), np.float)
middle_vector = np.zeros((3, 1), np.float)
minor_vector = np.zeros((3, 1), np.float)
mass_center = np.zeros((3, 1), np.float)

feature_extractor.getMomentOfInertia(moment_of_inertia)
feature_extractor.getEccentricity(eccentricity)
feature_extractor.getAABB(min_point_AABB, max_point_AABB)
feature_extractor.getEigenValues(major_value, middle_value, minor_value)    # 后面这三行似乎都不怎么管用，使用numpy数组直接作为参数的函数似乎都有这个问题。
feature_extractor.getEigenVectors(major_vector, middle_vector, minor_vector)
feature_extractor.getMassCenter(mass_center)



viewer = pcl.visualization.PCLVisualizer('3D Viewer')
viewer.setBackgroundColor(0.0, 0.0, 0.0)
viewer.addCoordinateSystem(1.0)
viewer.initCameraParameters()
viewer.addPointCloud(cloud, 'simple cloud')
viewer.addCube(min_point_AABB.x, max_point_AABB.x, min_point_AABB.y, max_point_AABB.y,
               min_point_AABB.z, max_point_AABB.z, 1.0, 1.0, 0.0, 'AABB')
viewer.setShapeRenderingProperties(5, 1, 'AABB')  # 点云用线框表示

position = np.array([[position_OBB.x], [position_OBB.y], [position_OBB.z]],
                    np.float)
quat = pclpy.pcl.vectors.Quaternionf()
viewer.addCube(position, quat, max_point_OBB.x - min_point_OBB.x,
               max_point_OBB.y - min_point_OBB.y, max_point_OBB.z - min_point_OBB.z, "OBB")
viewer.setShapeRenderingProperties(5, 1, "OBB")

center = pcl.point_types.PointXYZ()
center.x, center.y, center.z = mass_center[0], mass_center[1], mass_center[2]

x_axis = pcl.point_types.PointXYZ()
x_axis.x, x_axis.y, x_axis.z = major_vector[0] + mass_center[0],\
                               major_vector[1] + mass_center[1],\
                               major_vector[2] + mass_center[2]

y_axis = pcl.point_types.PointXYZ()
y_axis.x, y_axis.y, y_axis.z = middle_vector[0] + mass_center[0],\
                               middle_vector[1] + mass_center[1],\
                               middle_vector[2] + mass_center[2]

z_axis = pcl.point_types.PointXYZ()
z_axis.x, z_axis.y, z_axis.z = minor_vector[0] + mass_center[0], \
                               minor_vector[1] + mass_center[1], \
                               minor_vector[2] + mass_center[2]
viewer.addLine(center, x_axis, 1.0, 0.0, 0.0,  "major eigen vector")
viewer.addLine(center, y_axis, 0.0, 1.0, 0.0, "middle eigen vector")
viewer.addLine(center, z_axis, 0.0, 0.0, 1.0, "minor eigen vector")

while not viewer.wasStopped():
    viewer.spinOnce(10)

2. 说明

现在让我们研究一下这段代码的目的是什么。前几行将被省略，因为它们很明显。

# 加载点云
cloud = pcl.PointCloud.PointXYZ()
reader = pcl.io.PCDReader()
reader.read("../../data/min_cut_segmentation_tutorial.pcd", cloud)

只是从 .pcd 文件加载云。

feature_extractor = pcl.features.MomentOfInertiaEstimation.PointXYZ()
feature_extractor.setInputCloud(cloud)
feature_extractor.compute()

这是pcl::MomentOfInertiaEstimation类的实例化。紧接着我们设置输入点云并开始计算过程。

moment_of_inertia = pcl.vectors.Float()
eccentricity = pcl.vectors.Float()

min_point_AABB = pcl.point_types.PointXYZ()
max_point_AABB = pcl.point_types.PointXYZ()
min_point_OBB = pcl.point_types.PointXYZ()
max_point_OBB = pcl.point_types.PointXYZ()
position_OBB = pcl.point_types.PointXYZ()

rotational_matrix_OBB = np.zeros((3, 3), np.float)
major_value, middle_value, minor_value = 0.0, 0.0, 0.0
major_vector = np.zeros((3, 1), np.float)
middle_vector = np.zeros((3, 1), np.float)
minor_vector = np.zeros((3, 1), np.float)
mass_center = np.zeros((3, 1), np.float)

这是我们声明存储描述符和边界框所需的所有必要变量。

feature_extractor.getMomentOfInertia(moment_of_inertia)
feature_extractor.getEccentricity(eccentricity)
feature_extractor.getAABB(min_point_AABB, max_point_AABB)
feature_extractor.getEigenValues(major_value, middle_value, minor_value)    # 后面这三行似乎都不怎么管用，使用numpy数组直接作为参数的函数似乎都有这个问题。
feature_extractor.getEigenVectors(major_vector, middle_vector, minor_vector)
feature_extractor.getMassCenter(mass_center)

获取描述符和其他属性。

注意，getEigenValues()，getEigenVectors()，getMassCenter()这三个函数似乎没有起作用，使用numpy数组直接作为参数的函数似乎都有这个问题，前面几例子中求质心的时候也碰到过。

所以事实上，本教程只对 AABB进行了可视化，对于OBB，暂不能实现。后续有时间了，可以用numpy实现一下。

viewer = pcl.visualization.PCLVisualizer('3D Viewer')
viewer.setBackgroundColor(0.0, 0.0, 0.0)
viewer.addCoordinateSystem(1.0)
viewer.initCameraParameters()
viewer.addPointCloud(cloud, 'simple cloud')
viewer.addCube(min_point_AABB.x, max_point_AABB.x, min_point_AABB.y, max_point_AABB.y,
               min_point_AABB.z, max_point_AABB.z, 1.0, 1.0, 0.0, 'AABB')
viewer.setShapeRenderingProperties(5, 1, 'AABB')  # 点云用线框表示

创建PCLVisualizer用于结果可视化的类实例。在这里，我们还添加了云和 AABB 以进行可视化。我们设置渲染属性，以便使用线框显示立方体，因为默认使用实心立方体。

参考setShapeRenderingProperties()参数

position = np.array([[position_OBB.x], [position_OBB.y], [position_OBB.z]],
                    np.float)
quat = pclpy.pcl.vectors.Quaternionf()
viewer.addCube(position, quat, max_point_OBB.x - min_point_OBB.x,
               max_point_OBB.y - min_point_OBB.y, max_point_OBB.z - min_point_OBB.z, "OBB")
viewer.setShapeRenderingProperties(5, 1, "OBB")

OBB 的可视化稍微复杂一些。所以在这里我们从旋转矩阵创建一个四元数，设置 OBB 位置并将其传递给可视化器。

这里旋转矩阵转四元数尚未实现。

center = pcl.point_types.PointXYZ()
center.x, center.y, center.z = mass_center[0], mass_center[1], mass_center[2]

x_axis = pcl.point_types.PointXYZ()
x_axis.x, x_axis.y, x_axis.z = major_vector[0] + mass_center[0],\
                               major_vector[1] + mass_center[1],\
                               major_vector[2] + mass_center[2]

y_axis = pcl.point_types.PointXYZ()
y_axis.x, y_axis.y, y_axis.z = middle_vector[0] + mass_center[0],\
                               middle_vector[1] + mass_center[1],\
                               middle_vector[2] + mass_center[2]

z_axis = pcl.point_types.PointXYZ()
z_axis.x, z_axis.y, z_axis.z = minor_vector[0] + mass_center[0], \
                               minor_vector[1] + mass_center[1], \
                               minor_vector[2] + mass_center[2]
viewer.addLine(center, x_axis, 1.0, 0.0, 0.0,  "major eigen vector")
viewer.addLine(center, y_axis, 0.0, 1.0, 0.0, "middle eigen vector")
viewer.addLine(center, z_axis, 0.0, 0.0, 1.0, "minor eigen vector")