[人工智能]机器学习（八） ----增强学习AdaBoost（python实现简单数字分类）

增强学习AdaBoost

6.1 增强学习 AdaBoost

• 各个科室医生对患者进行会诊，各个科室的医生联合诊断要比一个科室的医生诊断的更全面准确。假设每个医生的诊断对应的是一个“弱化学习”，而多个弱化学习组合之后就得到了一个“强化了的学习”结果，这个过程就比较适合采用增强学习AdaBoost来实现。

6.2 集成方法

集成方法通过组合多个基分类器来完成学习任务。

 集成方法分类：
 1. Bagging ———— 对训练数据采用自举采样（Bootstrap Sampling）
 2. Boosting ———— 采用重赋权（reweighting）法迭代地训练基分类器

1. Bagging算法从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping算法抽取n个训练样本，每次使用一个训练得到一个模型，k个训练集共得到k个模型。对于分类问题，将得到的k个模型采用投票的方式得到分类结果。
2. Bootstraping算法原理：重复地在一个样本集合中采集n个样本，针对每个子样本集进行统计学习，获得假设H，将若干个假设进行组合，形成最终的假设，将最终的假设用于具体的分类任务。

6.3 Boosting 算法

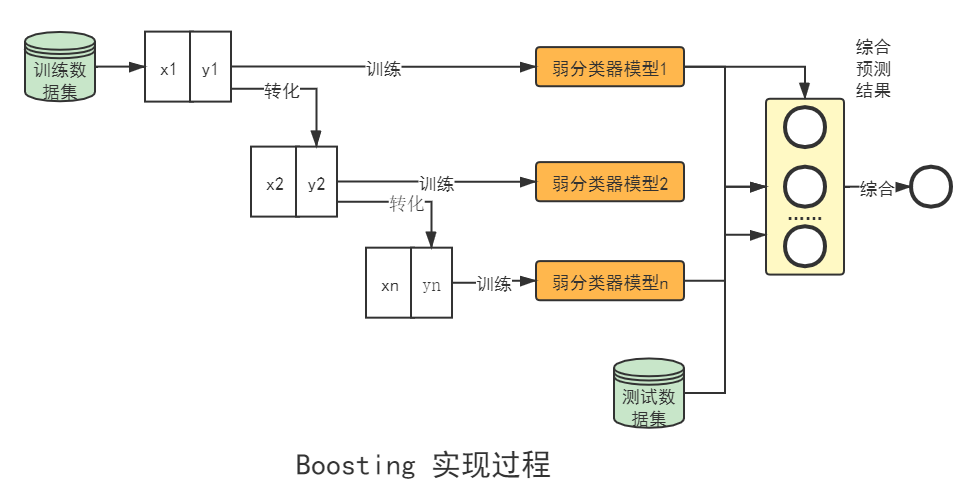
• Boosting是一种框架算法，拥有如AdaBoost、GradientBoosting、LogitBoost等系列算法。这些算法的主要区别在于其三要素选取的函数不同。Boosting的实现过程如下图所示，训练过程为阶梯状，弱分类器按次序训练，为了提高效率在实际使用中通常并行操作，弱分类器的训练数据集按照某种策略每次都进行一定的转化，最后将弱分类器组合成一个强分类器，对测试数据集进行分类。
  

6.4 AdaBoost 算法

自适应算法（Adaptive Boosting，AdaBoost）是一种迭代算法，核心思想和Boosting算法类似，是针对同一个训练集训练不同的弱分类器，然后将这些弱分类器组合成一个强分类器来完成分类的过程。

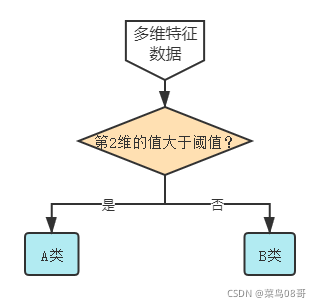
6.4.1 单层决策树方式的弱分类器

6.4.2 AdaBoost 分类器的权重

• AdaBoost算法中包括数据的权重和弱分类器的权重。

• 数据的权重用于弱分类器寻找决策点，使得其分类误差最小。

• 弱分类器权重越大说明该弱分类器在最终决策时拥有更大的发言权。

• 最终投票表决分类结果，需要根据弱分类器的权重来加权投票，弱分类器的错误率越低，其权重就越高。

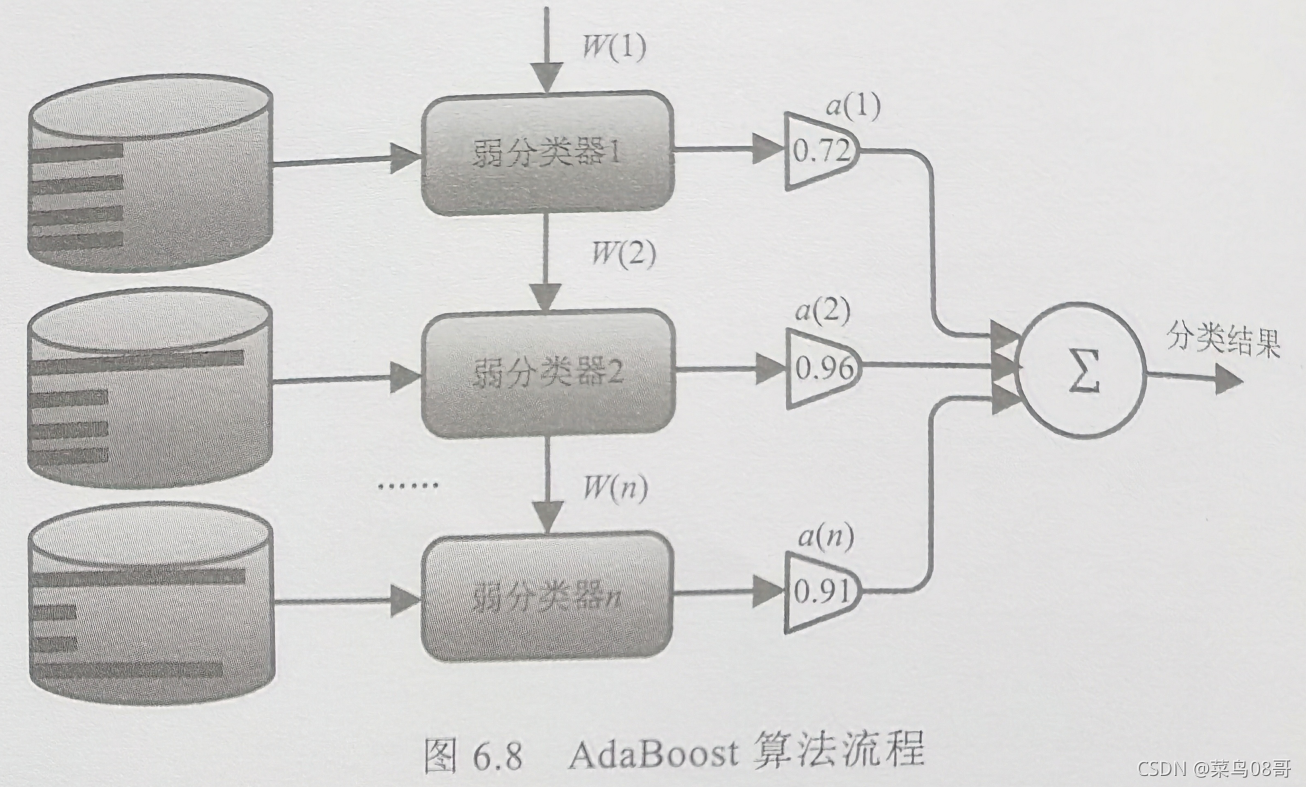
6.4.2 AdaBoost 算法流程

AdaBoost 算法流程如图所示。从图中可以看出, AdaBoost 的自适应在于引入权值的处理方式。前一个基本分类器被错误分类的样本权值会增大,而正确分类的样本权值会减小,并再次用于训练下一个基本分类器。同时,在每一轮迭代中加入一个新的弱分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器。对于准确率较高的弱分类器,加大其权重;对于准确率较低的弱分类器,减小其权重。

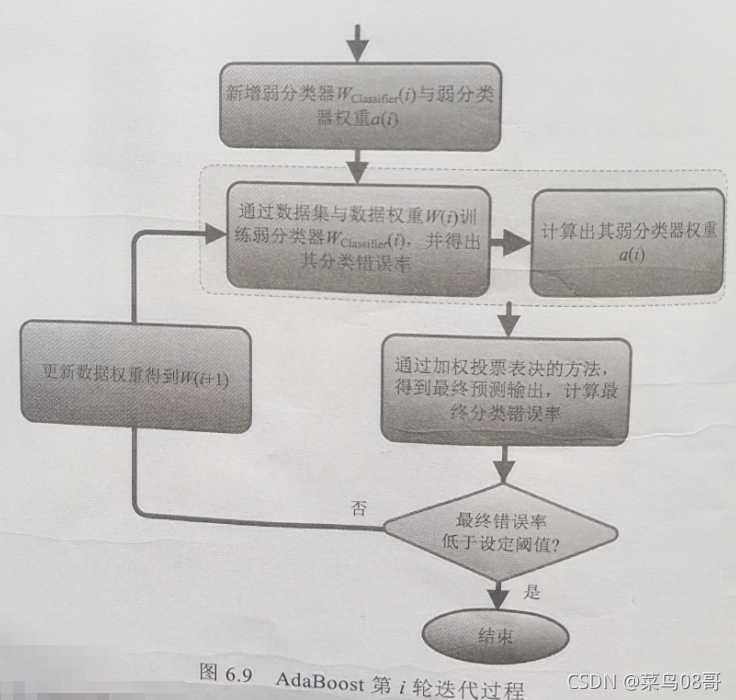
第 i 轮迭代所要完成的工作如图所示。需要注意设置一个阈值(如 LimitErrorValue =3%),如果最终分类错误率低于 LimitErrorValue ,那么该步迭代结束;如果最终错误率高于设定的值 LimitErrorValue ,那么更新数据权重得到 W (i+1),再次进行计算,直到满足分级类错误率低于设定的值 LimitErrorValue 。

6.5 AdaBoost的优缺点

• 优点：精度很高的分类器，可以使用各种方法构建子分类器，AdaBoost算法提供的是框架，弱分类器构造极其简单，不用担心过度拟合。

• 缺点：容易受到噪声干扰，这也是大部分算法的缺点，训练时间过长，执行效果依赖于弱分类器选择。

6.6 AdaBoost 实现数字简单分类

import math
import numpy as np
import matplotlib.pyplot as plt


# 产生弱分类器
def generate_G1(x):  # 定义分类器G1
    if x < 2.5:
        return 1
    if x > 2.5:
        return -1


def generate_G2(x):
    if x < 8.5:
        return 1
    if x > 8.5:
        return -1


def generate_G3(x):
    if x < 5.5:
        return -1
    if x > 5.5:
        return 1


# 定义函数，求G（X）在数据集上的误差率
def cal_error_G(X, Y, week_G, w_list):
    error_G = sum([w_list[i] for i in range(len(X)) if Y[i] != week_G(X[i])])
    # 返回误差率
    return error_G


# 计算所有弱分类器的误差，选择误差最小的弱分类器的下标和最小误差的值
def select_min_G(X, Y, w_list, week_G_list):
    error_list = [cal_error_G(X, Y, week_G, w_list) for week_G in week_G_list]
    # 循环得到误差集
    min_value = min(error_list)
    return error_list.index(min_value), min_value


# 计算归一化因子Z
def cal_Z(X, Y, G_values, w_list, alpha):
    Z = sum([w_list[i] * math.exp(-alpha * Y[i] * G_values[i]) for i in range(len(X))])
    return Z


# 更新权重
def update_w(X, Y, week_G, w_list, alpha):
    # 先计算出G（x）具体的值
    G_values = list(map(week_G, X))
    # 计算归一化参数
    z = cal_Z(X, Y, G_values, w_list, alpha)
    for i in range(len(X)):
        w_list[i] = w_list[i] * math.exp(-alpha * Y[i] * G_values[i])  # 根据公式更新权重值
        w_list[i] /= z
    return z


# 计算预测值
def predict_values(X, week_G_list, alpha_list, select_G_list):
    # 已经计算完成的alpha个数
    n = len(alpha_list)
    my_week_G = [week_G_list[i] for i in select_G_list]
    # 定义G_X_list，是一个3行10列的数组，每一行是Gi（x）的结果
    G_X_list = []
    for i in range(n):
        G_X_list.append(list(map(my_week_G[i], X)))
    # print(G_X_list)
    # print(alpha_list)

    G_X_list = np.array(G_X_list)
    alpha_array = np.array(alpha_list)
    # 需要alpha1*G_X_array矩阵的第一行，需要alpha2*G_X_array矩阵的第二行……
    # 通过title拼接并转置后，得到3行10列的矩阵，第一行均为alpha1，第二行均为alpha2……
    tmp = np.tile(alpha_array, (len(X), 1)).T
    # 对应位置元素乘*G_X_array
    result_array = tmp * G_X_list
    # print(result_array)

    predict_list = np.sum(result_array, axis=0)
    # print(predict_list)

    sign = lambda x: 1 if x > 0 else -1 if x < 0 else 0
    final_list = list(map(sign, list(predict_list)))
    # print(predict_list)
    return predict_list, final_list


# 计算alpha的值
def cal_alpha(error_value):
    return 0.5 * math.log((1 - error_value) / error_value)


# 初始化数据x为0~9
X = range(10)
Y = [1, 1, 1, -1, -1, -1, 1, 1, 1, -1]
# 点的数量为10
N = len(X)
# 初始权重均为0.1
w_list = [0.1] * 10
# 保存三个弱分类器的list
week_G_list = [generate_G1, generate_G2, generate_G3]
# 保存选择的弱分类器顺序的list
select_G_list = []

alpha_list = []

final_list = []

while final_list != Y:
    min_G_index, min_error = select_min_G(X, Y, w_list, week_G_list)
    select_G_list.append(min_G_index)
    selected_G = week_G_list[min_G_index]
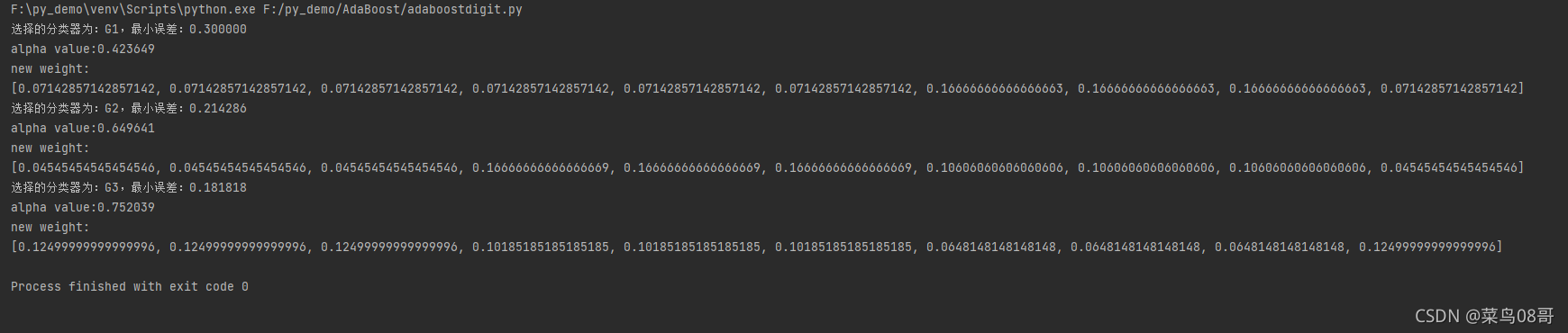
    print('选择的分类器为：G%d，最小误差：%f' % (min_G_index + 1, min_error))

    alpha = cal_alpha(min_error)
    alpha_list.append(alpha)
    print('alpha value:%f' % alpha)
    # 更新权重分布
    update_w(X, Y, selected_G, w_list, alpha)
    print('new weight:')
    print(w_list)

    # 计算最新模型的预测值
    predict_list, final_list = predict_values(X, week_G_list, alpha_list, select_G_list)

    # print(final_list)
    # print(final_list == Y)

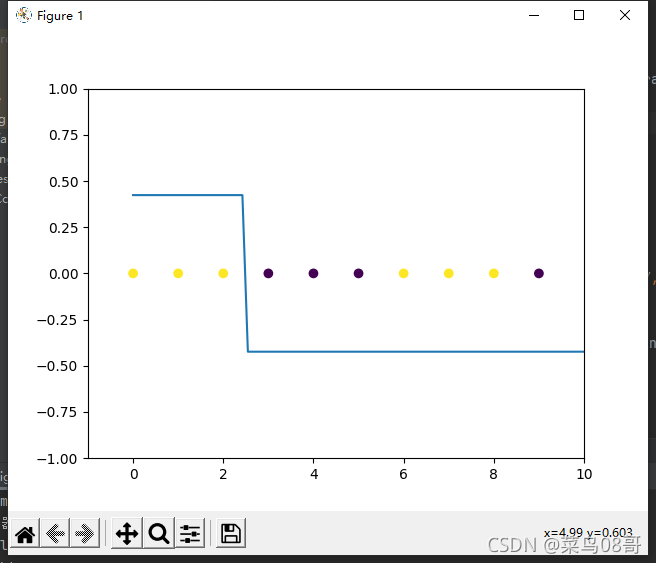
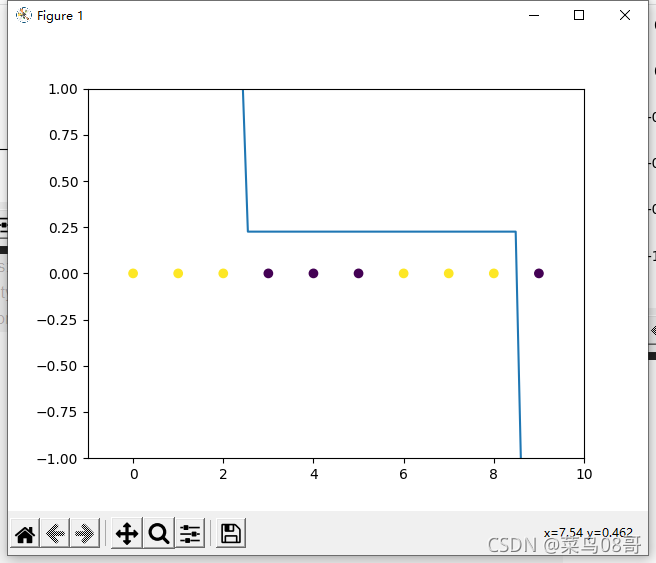
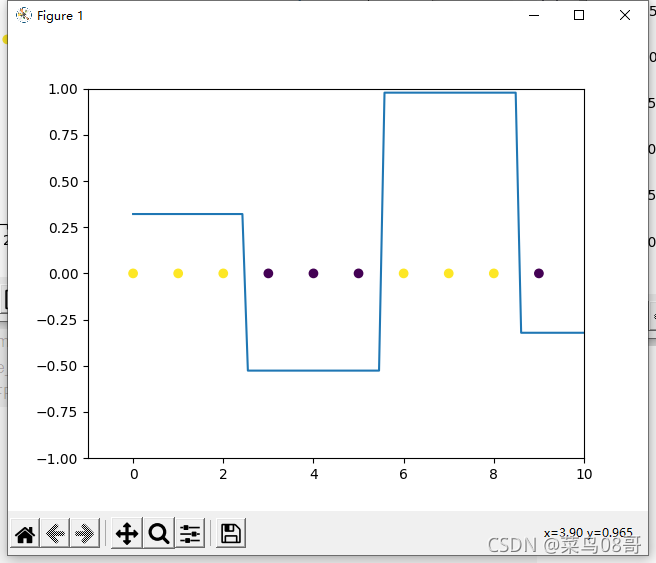
    plt.scatter(X, [0.0] * 10, c=Y)

    plt.xlim((-1, 10))
    plt.ylim((-1, 1))

    axis_x = np.linspace(0, 12, 100)
    # 获取函数值，存在axis_y中
    axis_y, my_final_list = predict_values(axis_x, week_G_list, alpha_list, select_G_list)
    plt.plot(axis_x, axis_y)
    plt.show()