本系列文章旨在对一些机器学习的基础算法进行精简的讲解
欢迎您关注后续的文章,内容问题或催更请私信
基本学习算法(1)一一线性回归
基本学习算法(2)一一决策树
基本学习算法(1)一一线性回归
??基于方程或数学运算而建立模型的算法–根据输入属性所取的值生成一个连续的值来表示输出–被称为回归算法。当我们想为优化结果提供选择时,我们通常使用回归技术。这些算法的输入可以是连续值或离散值(取决于算法),而输出是一个连续的值。
??我们来理解一下线性回归: 假设你要求一名小学生通过增加体重的顺序来安排他班上所有的学生,而不问他们的体重。你认为这个学生会做什么?
他会在视觉上分析学生的身高和体型,并将这些可见的参数组合起来。在这里,学生已经发现身高和体型与体重相关,这看起来像下面的等式。
??线性回归用于根据连续变量估计实际值。在这里,我们通过拟合最佳直线来建立自变量和因变量之间的关系。这个最佳拟合直线被称为回归直线,由以下线性方程表示:
????????
Y
=
a
?
X
+
b
Y=a*X+b
Y=a?X+b
其中,
Y
Y
Y是因变量,
a
a
a是斜率,
X
X
X是自变量,
b
b
b是截距。通过最小化数据点与回归线之间距离的平方和,得到系数a和b。
示例一:最简单的例子开始
??给定3对(x,y)训练数据:(2,4)、(5,1)、(8,9)进行函数建模,发现目标变量y和输入变量x之间的关系。

这一模型最为简单,如下所示:
????????
Y
=
a
?
X
+
b
Y=a*X+b
Y=a?X+b
通过运用该简单的线性函数,可模拟x和y之间的关系。关键在于该函数不仅与输入变量x成线性关系,而且与参数a、b成线性关系。
当前目标是确定最符合训练数据的参数a和b的值。
这可通过测量每个输入x的实际目标值y和模型f(x)之间的失配来实现,并将失配最小化。这种失配(=最小值)被称为误差函数。
有多种误差函数可供选择,但其中最简单的要数RSS,即每个数据点x对应的模型f(x)与目标值y的误差平方和。
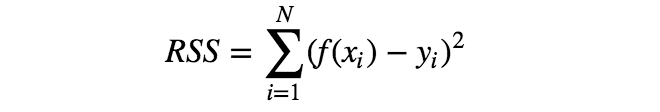
利用误差函数的概念,可将“确定最符合训练数据的参数a、b”改为“确定参数a、b,使误差函数最小化”。
计算一下训练数据的误差函数。

上面的等式就是要求最小值的误差函数。但是,怎样才能找到参数a、b,得到此函数的最小值呢?为启发思维,需要将该函数视觉化。

从上方的3D图来看,人们会本能地猜测该函数为凸函数。凸函数的优化(找到最小值)比一般数学优化简单得多,因为任何局部最小值都是整个凸函数的最小值。(简单来讲,就是凸函数只有一个最小点,例如“U”的形状)由于凸函数的这种特性,通过简单求解如下的偏微分方程,便可得到使函数最小化的参数。

下面解下之前的例子吧。

通过求解上面的等式,得到 a = 5 / 6 、 b = 1 / 2 a = 5/6、b = 1/2 a=5/6、b=1/2。因此,第一个模型(最小化RSS)如下所示:
?????????????? Y = 5 / 6 ? X + 1 / 2 Y=5/6*X+1/2 Y=5/6?X+1/2

示例2:简单的弯曲模型
现在,对于相同的数据点,可考虑如下的另一模型:
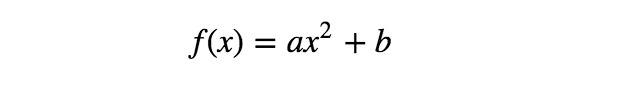
如上所示,该模型不再是输入变量 x x x的线性函数,但仍是参数 a 、 b a、b a、b的线性函数。
下面看下这一变化对模型拟合过程的影响。我们将使用与前一示例相同的误差函数——RSS。

如上所示,等式看起来与前一个非常相似。(系数的值不同,但方程的形式相同。)该模型的可视化图像如下:

两个模型的形状看起来也很相似,仍然是凸函数。但秘密在于,当使用训练数据计算误差时,输入变量作为具体值给出(例如,x2的值在数据集中给定为22、52和82,即(2,4)、(5,1)、(8,9))。因此,无论输入变量的形式多复杂(例如x、x2、sin(x)、log(x)等…),给定的值在误差函数中仅为常数。
误差函数的第二个模型也是凸函数,因此可通过与前一示例完全相同的过程找到最佳参数。
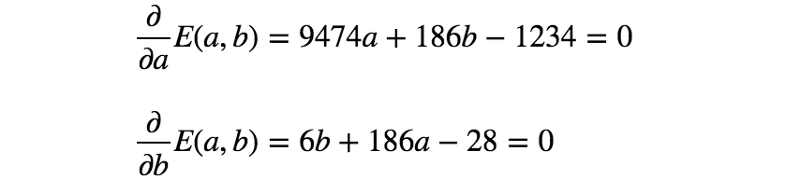
通过求解上面的等式,得到 a = 61 / 618 、 b = 331 / 206 a = 61/618、b = 331/206 a=61/618、b=331/206。所以,第二个模型如下所示:
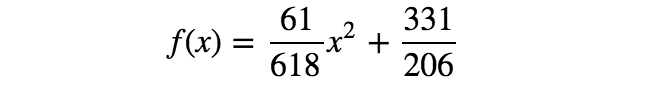

结论:线性回归模型的线性假设
上述2个例子的求解过程完全相同(且非常简单),即使一个为输入变量x的线性函数,一个为x的非线性函数。两个模型的共同特征是两个函数都与参数a、b成线性关系。这是对线性回归模型的线性假设,也是线性回归模型数学单性的关键。
上面2个模型非常简单,但一般而言,模型与其参数的线性假设,可保证RSS始终为凸函数。通过求解简单偏微分方程,得到最优参数,这就是线性假设至关重要的原因。