[人工智能]Mel频率倒谱系数-MFCC

MFCC：Mel频率倒谱系数的缩写。

目的：模拟人耳对不同频率语音的感知

Mel频率和Hz频率的关系

人类对不同频率语音有不同的感知能力:

• 1kHz以下，与频率成线性关系。
• 1kHz以上，与频率成对数关系。

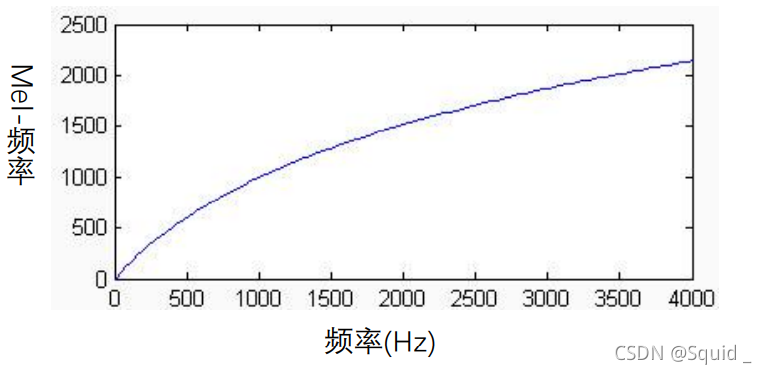
Mel频率倒谱系数(MFCC)则是利用它们之间的这种关系，计算得到的Hz频谱特征。

由于Mel频率与Hz频率之间非线性的对应关系，使得MFCC随着频率的提高，其计算精度随之下降。因此，在应用中常常只使用低频MFCC，而丢弃中高频MFCC。

$$F_{mel}=2595lg(1+f/700)$$
$F_{mel}$是以美尔（Mel）为单位的感知频率；f是以Hz为单位的实际频率。

Mel滤波器组

具体频率组的公式后面再说

在matlab中有个voicebox工具箱中有一个melbankm函数可用于计算Mel滤波器组。

h=melbankm(p,n,fs,fl,fh,w);
%{
fs是采样频率
fh是设计滤波器最高频率(用fs进行归一，一般为0)
fl是设计滤波器最低频率(用fs进行归一，一般为0.5)
p是在fl和fh之间设计mel滤波器的个数
n是一帧FFT后数据的长度
w是窗函数，'t'是三角窗，'n'和'm'是海明窗和汉宁窗
输出h是滤波器的频域响应，是一个p*(n/2+1)的数组，p个滤波器就有p个滤波器的频域响应，每个滤波器的响应曲线长为n/2+1，相当于取正频率的部分
}%

我们可以用代码的形式画出mel滤波器组的样子：

% pr3_3_1 
clear all; clc; close all;

% 调用melbankm函数,在0-0.5区间设计24个Mel滤波器,用三角形窗函数
bank=melbankm(24,256,8000,0,0.5,'t');
bank=full(bank);
bank=bank/max(bank(:));              % 幅值归一化

df=8000/256;                         % 计算分辨率
ff=(0:128)*df;                       % 频率坐标刻度
for k=1 : 24                         % 绘制24个Mel滤波器响应曲线
    plot(ff,bank(k,:),'k','linewidth',2); hold on;
end
hold off; grid;
xlabel('频率/Hz'); ylabel('相对幅值')
title('Mel滤波器组的频率响应曲线')

得出下图

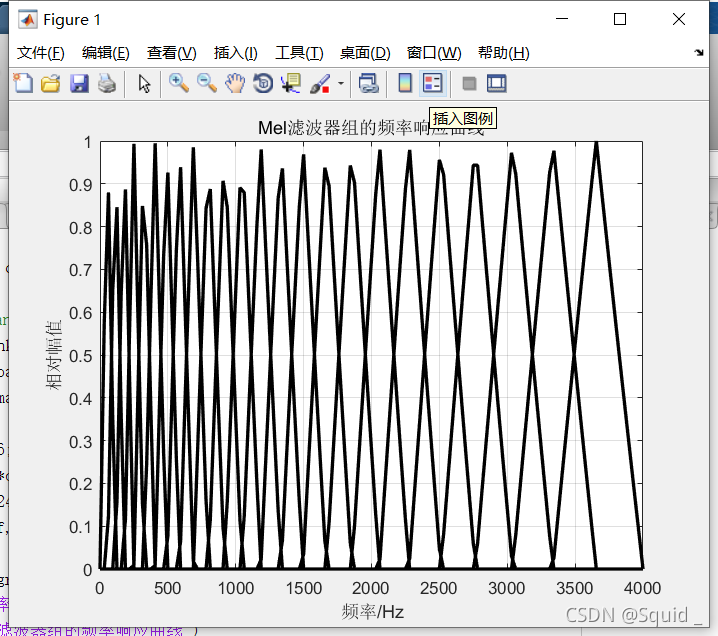
mfcc特征参数的提取

步骤：

1、预处理（预加重、分帧、加窗）

2、快速傅里叶变换

3、计算谱线能量

4、计算通过Mel滤波器的能量

5、计算DCT倒谱

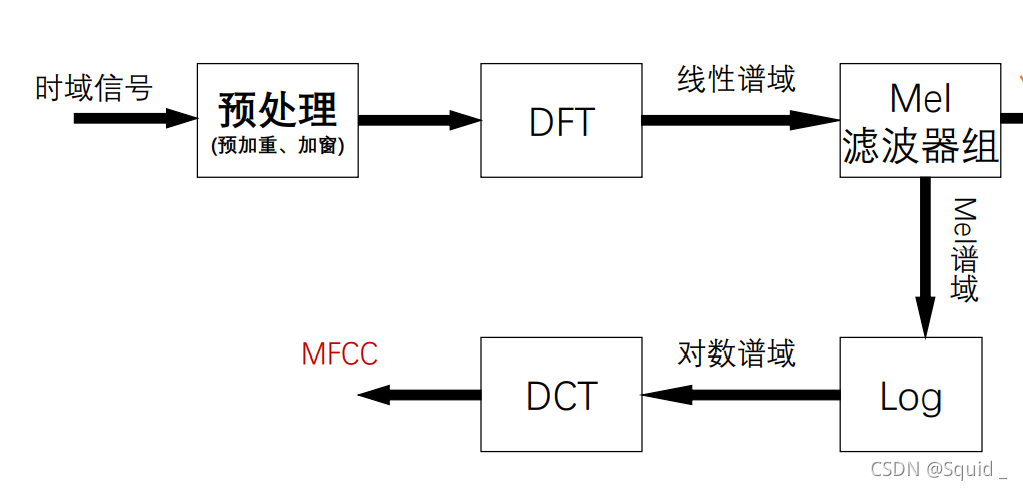
1、预处理

之前讲过分帧分窗了

预加重：目的是为了补偿高频分量的损失，提升高频分量。预加重的滤波器常设为
$$H(z)=1?a{z}^{?1}$$
式中，a为一个常数。

分帧：由于语音信号是一个准稳态信号，把它分成较短的帧，在每一帧中可将其看做稳态信号，可用处理稳态信号的方法来处理。同时，为了使一帧到另一帧之间参数能较平稳的过渡，在两帧之间互相有部分重叠。

加窗：目的是减少频域中的泄漏，将对每一帧语音乘以汉明窗或海宁窗。语音信号处理x(n)经处理后为$x_i(m)$,其中下标为第i帧。

2、快速傅里叶变换

将时域数据变成频域数据
$$X(i,k)=FFT(x_i(m))$$

3、计算谱线能量

对每一帧FFT后的数据计算谱线的能量：
$$E(i,k)=[X(i,k){]}^2$$

4、计算通过Mel滤波器的能量

把求出的每帧谱线能量谱通过Mel滤波器，并计算在该Mel滤波器中的能量。在频域中相当于把每帧的能量谱E(i,k)(其中i表示第i帧，k表示频谱中第k条谱线)与滤波器的频域响应$H_m(k)$相乘并相加：
$$S(i,m)=\sum _{k=0}^{N?1}E(i,k)H_{m}K,0\le m<M$$

5、计算DCT倒谱

FFT倒谱$\hat{x}(n)$为:
$$\hat{x}(n)=F{T}^{?1}[\hat{X}(k)]$$
式中，
$$\hat{X}(k)=lnFT[x(n)]=lnX(k)$$
而序列x(n)的DCT为：
$$X(k)=\sqrt{\frac{2}{N}}\sum _{n=0}^{N?1}C(k)x(n)cos[\frac{\pi (2n+1)k}{2N}],k=0,1,?,N?1$$
式中，参数N是序列x(n)的长度，C(k)是正交因子，可表示为：
$$C(k)=\{\begin{array}{l}\frac{\sqrt{2}}{2}，k=0\\ 1，k=1,2,?,N?1\end{array}$$
DCT倒谱和FFT倒谱很相似。把mel滤波器的能量取对数后，再计算DCT：
$$mfcc(i,n)=\sqrt{\frac{2}{M}}\sum _{m=0}^{M?1}log[S(i,m)]cos[\frac{\pi n(2m?1)}{2M}],k=0,1,?,N?1$$
式中S(i,m)是第4步求出的Mel滤波器能量。m是指第m个Mel滤波器，i是指第i帧，n是DCT后的谱线。

这样就计算出了MFCC参数。

6、倒谱提升窗口

在为每帧数据计算出K阶MFCC参数后，通常还要为这K个系数分别乘以不同的权系数ω，实际上是一个短的窗口。
$${\omega }_m=1+\frac{K}{2}sin(\frac{\pi m}{K}),1\le m\le K$$

$${\hat{c}}_m={\omega }_m{C}_m$$

7、差分倒谱参数

标准的MFCC参数只反映了语音参数的静态特性，而人耳对语音的动态特征更为敏感，如何获得反映语音动态变化的参数，通常是用差分倒谱参数来描述这种特性。

差分参数的计算公式如下：
$$d(n)=\frac{1}{\sqrt{{\sum }_{i=?k}^k{i}^2}}\sum _{i=?k}^{k}i?c(n+i)$$
这里c和d都表示一帧语音参数，k为常数，通常取2，这时差分参数就称为当前帧的前两帧和后两帧参数的线性组合。

由此公式可求出差分参数的一阶MFCC差分参数，用同样的公式对一阶差分参数进行计算，可以得到二阶差分MFCC参数。实际应用中，将MFCC参数和各阶差分参数合并为一个完整的矢量，作为一帧语音信号的参数。

mfcc代码

代码如下：

function ccc=mfcc_m(x,fs,p,frameSize,inc)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%                 function ccc=mfcc_m(x);
%对输入的语音序列x进行MFCC参数的提取，返回MFCC参数和一阶
%差分MFCC参数，Mel滤波器的个数为p，采样频率为fs
%对x每frameSize点分为一帧，相邻两帧之间的帧移为inc
% FFT的长度为帧长
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 按帧长为frameSize，Mel滤波器的个数为p，采样频率为fs
% 提取Mel滤波器参数，用汉明窗函数
bank=melbankm(p,frameSize,fs,0,0.5,'m');
% 归一化Mel滤波器组系数
bank=full(bank);
bank=bank/max(bank(:));

% DCT系数,12*p
for k=1:12
  n=0:p-1;
  dctcoef(k,:)=cos((2*n+1)*k*pi/(2*p));
end

% 归一化倒谱提升窗口
w = 1 + 6 * sin(pi * [1:12] ./ 12);
w = w/max(w);

% 预加重滤波器
xx=double(x);
xx=filter([1 -0.9375],1,xx);

% 语音信号分帧
xx=enframe(xx,frameSize,inc);
n2=fix(frameSize/2)+1;
% 计算每帧的MFCC参数
for i=1:size(xx,1)
  y = xx(i,:);
  s = y' .* hamming(frameSize);
  t = abs(fft(s));
  t = t.^2;
  c1=dctcoef * log(bank * t(1:n2));
  c2 = c1.*w'; % 倒谱提升
  m(i,:)=c2';
end

%差分系数
dtm = zeros(size(m));
for i=3:size(m,1)-2
  dtm(i,:) = -2*m(i-2,:) - m(i-1,:) + m(i+1,:) + 2*m(i+2,:);
end
dtm = dtm / 3;
%合并MFCC参数和一阶差分MFCC参数
ccc = [m dtm];
%去除首尾两帧，因为这两帧的一阶差分参数为0
ccc = ccc(3:size(m,1)-2,:);