[人工智能]梯度下降/牛顿法实现逻辑回归

数据集及完整代码详见此链接https://download.csdn.net/download/cc__cc__/28820647

一、训练数据可视化

1.读取训练数据

def read_train_data():
    x = []
    y = []
    with open("./逻辑回归数据.txt", 'r') as f:
        for line in f.readlines():
            data_list = line.strip('\n').split(',')
            x.append([1.0, float(data_list[0]), float(data_list[1])])
            y.append(float(data_list[-1]))
    f.close()
    x = np.asarray(x, dtype=np.double)
    y = np.asarray(y, dtype=np.double)
    return x, y

• 值得注意的是，每一个x都增加了一个分量1.0，即最终参数θ包含三个分量θ0，θ1，θ2，其中θ0对应截距。

2.训练数据可视化

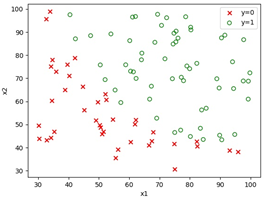
def plot_train_data(x, y):
    plt.figure()
    for i in range(x.shape[0]):
        if y[i] == 1:
            plt.scatter(x[i][1], x[i][2], c='none', marker='o', edgecolors='g', label='y=1') 
        else:
            plt.scatter(x[i][1], x[i][2], c='r', marker='x', label='y=0')
    plt.xlabel('x1')
    plt.ylabel('x2')
    # omit redundant legend
    handles, labels = plt.gca().get_legend_handles_labels()
    unique_label = OrderedDict(zip(labels, handles))
    plt.legend(unique_label.values(), unique_label.keys())
    plt.savefig("./plot_train_data.jpg")
    plt.show()

二、逻辑回归算法简介

def sigmoid(z):
    return 1/(1 + np.exp(-z))

def log_likehood(theta, x, y):
    l_theta = 0.0
    for i in range(x.shape[0]):
        l_theta += y[i] * np.log(sigmoid(np.inner(theta, x[i]))) + (1 - y[i]) * np.log(1 - sigmoid(np.inner(theta, x[i])))
    return l_theta

def cost_function(theta, x, y):
    L = log_likehood(theta, x, y)
    J = -L/x.shape[0]
    return J

三、梯度下降法实现逻辑回归

本次实验共尝试3种梯度下降方法，即批量梯度下降法、随机梯度下降法、小批量随机梯度下降法，其中单样本梯度计算代码如下：

def gradient(theta, x, y):
    return -(y - sigmoid(np.inner(theta, x))) * x

此外，3种方法参数θ的更新均使用theta = theta - alpha * batch_grad，代码详见gradient_descents.py

1.批量梯度下降法（BGD）

批量梯度下降法在更新参数时使用所有的样本来进行更新，运行train.py并传递相应的参数如下图所示。

以迭代400000次的结果为例，得到的cost function曲线如图3所示，可见整个过程都是收敛的趋势。通过图4的比较也可以看出迭代400000次时已经能够达到较好的二分类效果，但此方法的问题在于训练速度过于缓慢。

2.随机梯度下降法（SGD）

随机梯度下降法与批量梯度下降法原理类似，区别在于每次只随机选取一个样本求梯度更新参数。在实验中借助random.randint函数随机选择100个训练样本中的1个样本求梯度。

i = random.randint(0, 99)
batch_grad = gradient(theta, x[i], y[i])

为了便于比较，当SGD迭代与BGD相近的时间（1000s）时终止迭代，运行train.py并传递相应的参数如下图所示。

由于每次迭代只计算一个样本的梯度，所以SGD的迭代速度较快（共完成约555000次迭代），但是仅用一个样本决定梯度方向，导致迭代方向变化较大，不能很快的收敛到最优解，结果如图6、图7所示。

3.小批量梯度下降法（Mini-Batch-GD）

小批量梯度下降法是批量梯度下降法和随机梯度下降法的折中，对于m个样本选取其中的x（1＜x＜m）个样本进行迭代。在实验中借助random.sample函数随机选择100个训练样本中的10个样本求梯度。

index = random.sample(range(0, 99), 10)
for i in index:
    batch_grad += gradient(theta, x[i], y[i])

同样地，当mini-GD迭代与BGD相近的时间（1000s）时终止迭代，运行train.py并传递相应的参数如下图所示。

小批量梯度下降每次迭代只需计算10个样本的梯度，但实验结果表明mini-GD的迭代速度实际上与BGD相差不大，且逻辑回归的效果介于BGD和SGD之间。考虑到本实验所用训练集样本量并不大，总的来说，在3种梯度下降方法中使用BGD更合适。

四、牛顿法实现逻辑回归

使用牛顿法同样需要根据error×feature求出梯度：

def grad_matrix(theta, x, y):
	y = np.squeeze(y)
	error = sigmoid(np.inner(theta, x)) - y
	G = np.inner(error, x.T)
	return G

此外，需要表示出海森矩阵：

def hessian_matrix(theta, x):
    h = []
    for i in range(x.shape[0]):
        h += [sigmoid(np.inner(theta, x[i])) * (1 - sigmoid(np.inner(theta, x[i]))) * x[i]]
    H = np.dot(x.T, h)
    return H

在更新参数θ时涉及求海森矩阵（H）的逆矩阵，借助numpy中的函数实现：theta = theta - np.dot(np.linalg.pinv(H), batch_grad)，代码详见newton_methods.py

通过图12、图13可见牛顿法实现逻辑回归只需几次迭代即可得到较好的二分类效果，收敛速度明显快于梯度下降法。

五、借助Pytorch框架实现逻辑回归

除了上述实现方法，还可直接借助pytorch框架以torch.nn.BCEWithLogitsLoss()作为损失函数，分别调用Adam、RMSprop、Adagrad优化器实现逻辑回归。
也可参考之前的博客【Pytorch实战(四)】线性判决与逻辑回归