二次规划
在MATLAB中,quadprog是具有线性约束的二次目标函数的求解器。
quadprog 求由下式指定的问题的最小值
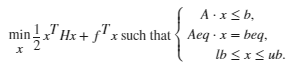
H、A 和 Aeq 是矩阵,f、b、beq、lb、ub 和 x 是向量。
其具体用法为:
x = quadprog(H,f)
x = quadprog(H,f,A,b)
x = quadprog(H,f,A,b,Aeq,beq)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub)
x =quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)
x =quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)
x = quadprog(problem)
[x,fval] = quadprog(___)
[x,fval,exitflag,output] = quadprog(___)
[x,fval,exitflag,output,lambda] = quadprog(___)
当解决一个具有线性约束的二次规划问题时:


要求解此问题,首先输入系数矩阵。
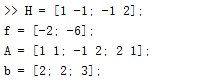
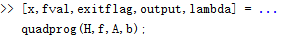
使用MATLAB语句为:
H = [1 -1; -1 2];
f = [-2; -6];
A = [1 1; -1 2; 2 1];
b = [2; 2; 3];
[x,fval,exitflag,output,lambda] = ...
quadprog(H,f,A,b);
x,fval %打印结果
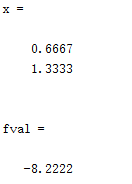
当使用python进行二次型求解时,采用qpsolvers库中的solve_qp函数进行求解:
进行库文件的安装
pip install cvxopt==1.2.6 cvxpy==1.1.11 Cython==0.29.22 ecos==2.0.7.post1 numpy osqp==0.6.2.post0 qdldl==0.1.5.post0 qpsolvers==1.7.0 quadprog==0.1.8 scipy scs==2.1.4 -i https://pypi.tuna.tsinghua.edu.cn/simple
from numpy import array
from qpsolvers import solve_qp
H=array([[1.,-1.],[-1.,2.]])
f=array([[-2.],[-6.]]).reshape((2,))
L=array([[1.,1.],[-1.,2.],[2.,1.]])
k=array([[2.],[2.],[3.]]).reshape((3,))
x = solve_qp(H, f, L,k)
print("QP solution: x = {}".format(x))
输出
QP solution: x = [0.66666667 1.33333333]