利用 python 实现 KNN 算法(自己实现 和 sklearn)
创作背景
昨天有个朋友请我帮他做一个 python 的作业,作业要求如下图(翻译过)

也就是:
给定了数据集,使用 KNN 算法完成下列目标
- 编写
自己的代码实现KNN并且用绘制图像 - 使用
sklearn绘制图像(使用KNeighborsClassifier进行分类)
绘制的图像效果如下

- 偷偷说一句:如果对我的答案和解析满意的话可不可以给我
点个赞,点个收藏之类的 Let's do it !!!
思路讲解
先开始我很懵,毕竟我也没怎么学过 KNN ,只是大概了解这个算法,想必来看文章的你也是有点不知所云,所以我们就先了解一下这个算法。
了解算法
KNN ,全称是 K-NearestNeighbors ,直译过来就是 K 个距离最近的邻居 ,专业术语是 K 最近邻分类算法 。
俗话说的好,物以类聚,人以群分 ,这个算法也是体现了这个思想,说的是每个样本的类别都可以用 离它最接近的 K 个邻近值的类别 来代表。
拿最常用的一个例子来说,看下边这一张图

我们要判断 绿色的圆形 也就是未知的数据属于哪个类别,我们就可以根据离它最近的几个点的类别来判断。
- 如果
k = 3,也就是我们要看离这个点最近的3个点(如实心?圈住的点),其中2 个是 红色三角形 ,1 个是 蓝色正方形 ,那我们就可以判断这个未知的点属于 红色三角形 ,因为离它最近的三个点中红色三角形的点数量多。 - 如果
k = 5,也就是我们要看离这个点最近的5个点(如虚线?圈住的点),其中3 个是 蓝色正方形 ,红色三角形 的数量还是2 个,这时候形势逆转,那现在我们就认为未知点属于 蓝色正方形 。
上边的例子应该很好理解,其他数据也是类似。
作业思路(自己实现)
知道了 KNN 是怎么回事了以后我们就可以来做作业了。
第一步
Of course,导库 ,这次我们用到的库有 numpy,矩阵操作;pandas ,读取数据;collections ,统计数量;matplotlib,绘图 。
import numpy as np
import pandas as pd
from collections import Counter
import matplotlib.pyplot as plt
第二步
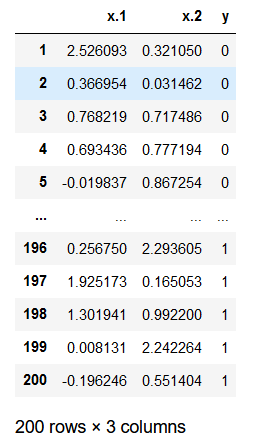
我们要 查看 一下作业 数据 ,并且进行 数据预处理 ,数据如下图所示(部分)
- 读取完毕后的数据,其中,
x.1和x.2分别是每个点的 横纵坐标 ,y是该点对应的 类别 ,取值为0和1。
- 数据预处理,即将点的坐标转换为
二维数组。np.concatenate进行矩阵合并,axis=1指定 按列合并 。代码如下(为了方便讲解代码逻辑,所以把一段长代码分为不同的行,文章后边也一样):
spots = np.concatenate(
[
np.array(df['x.1']).reshape(-1, 1),
np.array(df['x.2']).reshape(-1, 1)
],
axis=1
)
- 画一下
散点图,看一下数据分布,代码如下
for i, fig in enumerate([('#87CEEB', '.'), ('orange', 'x')]):
# 找到对应分类的点
data = df.where(df['y'] == i).dropna()
# 绘制散点图
plt.scatter(data['x.1'], data['x.2'], marker=fig[1], color=fig[0])
plt.show()

第三步
读取完数据后就到了第三步,利用 python 实现 knn 。
- 这个作业中模型函数是最基础的
线性模型:
y = β 0 + ∑ j = 1 p X j β j y={\beta}_{0} + \displaystyle \sum ^{p} _{j=1} {X}_{j} {\beta}_{j} y=β0?+j=1∑p?Xj?βj?
转换为矩阵形式:
y = X T β y = {X}^{T} \beta y=XTβ - 这里是将
β
0
{\beta}_{0}
β0? 作为第
0个数,对应x=1时y的取值,所以我们还需要将 X 扩展,并且第0个数为1。 - 这里我们计算点之间的
欧式距离,并以此作为评判标准。 - 为了提高代码的
复用性,我将算法封装成函数,参数为要预测的点的坐标和k值,代码如下:
def take_nearest(grid, k):
'''
对传入的点进行 knn 分类
:param grid: 点的坐标
:type grid : tuple
:param k: 邻居个数
:type k : int
:return : 点的分类
'''
# 计算所有已知点距离未知点的距离,即实现 欧氏距离 的计算
distance = np.sqrt(
np.sum((spots - grid) ** 2, axis=1)
)
# 类别判断
# 具体细节见下述
cate = Counter(
np.take(
df['y'],
distance.argsort()[:k]
)
).most_common(1)[0][0]
return cate
- 其中:
distance.argsort()得到 排序后的列表 的 对应数据索引,[:k]取 前 k 个 元素np.take根据第二个参数 条件 取第一个参数 数据 中对应的数据Counter计算序列中 每个类别出现的频率most_common(1)取 频率最高 的类别和数量
第四步
- 这函数也弄完了,可是这题目到底要用
KNN分类什么点呀? - 我当时已知没搞明白。后来,看了看上边要的效果图我才终于明白分类什么点。
- 如果你仔细看题目要求的图就会发现图的背景是
像素点,根据不同的分类,像素点的颜色也不同,代表两个不同的分类。 - 那我们就有
方向了(插一句,选对方向对于学习之路很重要,要不然会找不到前进的方向)。
这一步,我们应该 生成像素点 。图中的像素点之间的间隔为 0.2 ,所以我们可以 生成 两个差值为 0.2 的 等差数列 ,然后使用 np.meshgrid 生成网格点坐标矩阵。代码如下:
In[]: # 生成背景像素点
bg_x, bg_y = np.meshgrid(
np.arange(-3.0, 5.2, 0.2),
np.arange(-2.0, 3.2, 0.2)
)
# 拼接成二维矩阵
bg_spots = np.concatenate(
[
bg_x.reshape(-1, 1),
bg_y.reshape(-1, 1)
],
axis=1
)
bg_x, bg_y, bg_spots
---------------------------------------------------------------------------------
Out[]: (array([[-3. , -2.8, -2.6, ..., 4.6, 4.8, 5. ],
[-3. , -2.8, -2.6, ..., 4.6, 4.8, 5. ],
[-3. , -2.8, -2.6, ..., 4.6, 4.8, 5. ],
...,
[-3. , -2.8, -2.6, ..., 4.6, 4.8, 5. ],
[-3. , -2.8, -2.6, ..., 4.6, 4.8, 5. ],
[-3. , -2.8, -2.6, ..., 4.6, 4.8, 5. ]]),
array([[-2. , -2. , -2. , ..., -2. , -2. , -2. ],
[-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
[-1.6, -1.6, -1.6, ..., -1.6, -1.6, -1.6],
...,
[ 2.6, 2.6, 2.6, ..., 2.6, 2.6, 2.6],
[ 2.8, 2.8, 2.8, ..., 2.8, 2.8, 2.8],
[ 3. , 3. , 3. , ..., 3. , 3. , 3. ]]),
array([[-3. , -2. ],
[-2.8, -2. ],
[-2.6, -2. ],
...,
[ 4.6, 3. ],
[ 4.8, 3. ],
[ 5. , 3. ]]))
第五步
利用 第三步 封装的函数对每个像素点的类别进行判断,代码如下:
In[]: bg_spots_df = pd.DataFrame(
np.concatenate(
[
bg_spots,
np.array(
list(map(lambda x: take_nearest(x, 1), bg_spots))
).reshape(-1, 1)
],
axis=1
),
columns=data1.columns)
bg_spots_df
---------------------------------------------------------------------------------
Out[]: x.1 x.2 y
0 -3.0 -2.0 0.0
1 -2.8 -2.0 0.0
2 -2.6 -2.0 0.0
3 -2.4 -2.0 0.0
4 -2.2 -2.0 0.0
... ... ... ...
1061 4.2 3.0 1.0
1062 4.4 3.0 1.0
1063 4.6 3.0 1.0
1064 4.8 3.0 0.0
1065 5.0 3.0 0.0
1066 rows × 3 columns
其中:
list(map(lambda x: take_nearest(x, 1), bg_spots))是对每个像素点进行KNN 分类,并将结果存为列表,这是k=1的情况,如果要变化k值,则改为take_nearest(x, 【k 值】)np.array().reshape(-1, 1)将分类结果转换为n 行 1 列的二维矩阵np.concatenate()将背景点的坐标与分类进行对应pd.DataFrame()将结果转换为DataFrame,为了方便绘图
第六步(The Final Step)
这一步也是最后一步,进行 绘图 ,代码如下:
for i, fig in enumerate([('#87CEEB', '.'), ('orange', 'x')]):
# 查找对应分类的数据点
spot = data1.where(data1['y'] == i).dropna()
# 查找对应分类的背景点
bg_spot = bg_spots_df.where(bg_spots_df['y'] == i).dropna()
# 绘制散点图
plt.scatter(bg_spot['x.1'], bg_spot['x.2'], s=0.2, color=fig[0])
plt.scatter(spot['x.1'], spot['x.2'], marker=fig[1], color=fig[0])
plt.show()
绘制的图像如下
k = 1

k = 15

效果还算不错😁
使用 sklearn 实现
这就简单许多,因为 sklearn 已经封装好了 KNN 算法,我们只需要调用即可,代码如下:
from sklearn.metrics import accuracy_score
from sklearn.metrics import mean_squared_error
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
# 将数据分为训练集和测试集,用来测试模型分类正确率
train_set, test = train_test_split(deepcopy(df), test_size = 0.2, random_state = 42)
def train(k=1):
# 创建分类器
clf = KNeighborsClassifier(n_neighbors=k)
# 训练数据
clf.fit(train_set[train_set.columns[:-1]], train_set['y'])
# 测试数据
test_predictions = clf.predict(test[test.columns[:-1]])
print('Accuracy:', accuracy_score(test['y'], test_predictions))
print('MSE:', mean_squared_error(test['y'], test_predictions))
# 预测数据,绘图
for i, fig in enumerate([('#87CEEB', '.'), ('orange', 'x')]):
spots = pd.DataFrame(np.take(bg_spots, np.where(clf.predict(bg_spots) == i)[0], axis=0))
plt.scatter(spots[0], spots[1], s=0.2, marker=fig[1], color=fig[0])
结尾
以上就是我要分享的内容,因为学识尚浅,会有不足,还请各位大佬指正。
有什么问题也可在评论区留言。
