[人工智能]Tensorflow&numpy&keras最详细的学习笔记(附每一个函数的示例代码和练习程序）

笔者结合北京大学Tensorflow学习网课和一些个人理解对Tensorflow进行了系统化的学习和笔记总结，里面包括了从基础的张量创建到深入的进行构造BP,CNN,RNN等网络模型的Tensorflow_keras实现和改进，并利用北京大学Tensorflow学习网课中的样例进行了自我调整和实现。
本文可供和笔者一样的网络初学者使用和参考，也可供时间不允许，需要迅速使用网络框架的学者参考，如需查阅详细CNN，RNN，LSTM，DHNN等详细网络构造和数学推导，笔者这里推荐各位一本不错的书:《Neural Networks and Deep Learning》，编者邱锡鹏，机械工业出版。这里粗略的介绍了网络的构造和一些浅显的数学推导，如需了解神经网络构造和工作原理的读者，感兴趣的可以参考电子书籍《Neuronal DynamicsFrom single neurons to networks and models of cognition》，电子书原文地址如下：
https://neuronaldynamics.epfl.ch/index.html
北京大学Tensorflow学习网课原地址如下，如需要的读者可以自行查看
https://www.icourse163.org/learn/PKU-1002536002?tid=1462067447#/learn/announce
本文不包含严格数学推导，仅包含应用。
阅读本文需要先对神经网络的基本框架构造和基础计算方式有所了解，如需了解，可参考周志华《机器学习》中BP神经网络的工作方法和上述两本书中RNN,CNN的工作原理。
目前写到了BP，笔者会持续更新RNN和CNN的内容，希望大家支持！
下面进入正题

一、张量创建和张量转换

Tensorflow的张量定义如下：

1、tf.constant(张量内容，dtype=数据类型）

函数的用法解释和说明：

①常用的dtype示例如下：

当然不局限于表格里面这些，比如一些tf.string和tf.bool等不常用的笔者未列出，想要用的读者可以详细查找。
②张量内容可以是一维数值，二维向量，或者三维矩阵，n维向量···

example1:

tf.constant(35,dtype=tf.int64)#这是数的定义
tf.constant([1.1,2.2,3.3],dtype=tf.float32)#这是向量的定义
tf.constant([[1.1,2.2],[3.3,4.4]],dtype=tf.float32)#这是矩阵的定义

以此类推，你想要去定义多少维就可以定义多少维。
Tensorflow的张量转换函数如下：

2、tf.convert_to_numpy(要转换的数据名，dtype=数据类型）

由于日常生活中导入python的数据类型经常以numpy的np对象来导入，因此需要进行np和tf之间的数据转换。

example2:

import numpy as np
import tensorflow as tf
data=np.arange(0,10,1)
n_data=tf.convert_to_tensor(data,dtype=tf.int64)#数据转换为tf类型数据

二、Tensorflow常用函数

3、 tf.zeros(维度）tf.ones(维度）tf.fill(维度，指定填充值)

example3：

tf.zeros([2,2])#——生成2×2的零矩阵。
tf.ones(7)#——生成7个1，一维向量。
tf.fill([4,4],9)#——生成4×4的全9矩阵。

4、正态分布(截断与非截断）&均匀分布

①tf.random.normal(维度,mean=均值,stddev=标准差)

②tf.random.truncated_normal(维度,mean=均值,stddev=标准差)

③tf.random.uniform(维度,minval=最小值,maxval=最大值）

函数的用法解释和说明：

第一个是表示生成正态分布随机数的，第二个表示生成截断式正态分布随机数的，这里的截断式表示生成以均值为原点，两倍标准差为变化范围的正态分布数据,相当于截断了两边的尾。第三个函数为生成均匀分布[minval，maxval]的数据。

example4：

tf.random.normal([2,2],mean=5,stddev=1)
#2×2维正态分布随机数，满足均值是5，方差是1
tf.random.truncated_normal([2,2],mean=5,stddev=1)
#截断式正态分布，其余和上面一样。
tf.random.uniform([2,2],minval=-1,maxval=6)
#生成[-1,6]的均匀分布2×2矩阵数据。

5、其他常用的一些操作(加减乘除等)

①tf.cast(张量名称,dtype=数据类型)——张量强制转换

②tf.reduce_min(张量名称,axis=0 or 1)——求最小值，axis为0代表按列求（每一列的最小），axis为1代表按行求最小（即每一行的最小）。

③tf.reduce_max(张量名称,axis=0 or 1)——求最大值，axis为0代表按列求（每一列的最大），axis为1代表按行求（即每一行的最大）。

④tf.reduce_mean(张量名称,axis=0 or 1)——求平均值，axis为0代表按列求（每一列的平均值），axis为1代表按行求（即每一行的平均值）。

⑤tf.reduce_sum(张量名称,axis=0 or 1)——求和，axis为0代表按列求（每一列的和），axis为1代表按行求（即每一行的和

⑥tf.add(张量1,张量2)(张量1+张量2),tf.subtract(张量1,张量2)(张量1-张量2),tf.multiply(张量1,张量2)(张量1×张量2),tf,divide(张量1,张量2)(张量1÷张量2),tf.square(张量1)(张量1平方),tf.pow(张量1,张量2)(张量1的张量2次幂),tf.sqrt(张量1)(张量1开方),tf.matmul(张量1,张量2)(张量1×张量2的矩阵乘法,tf.greater(张量1,张量2)返回张量一是否大于张量二的bool阵。

⑦tf.where(条件语句，A，B）——条件语句为真执行A，否则执行B

example5：

import tensorflow as tf
tf.compat.v1.disable_eager_execution()#2.0版本没办法兼容Session
data=tf.constant([[1.1,2.2],[3.3,4.4],[5.5,6.6]],dtype=tf.float32)
tf.cast(data,dtype=tf.float64)#强制转换数据
tf.reduce_min(data,axis=1)#按列求最小，结果为[1.1,3.3,5.5]
tf.reduce_min(data,axis=0)#按行求最小，结果为[1.1,2.2]
tf.reduce_max(data,axis=1)#按列求最大，结果为[2.2，4.4，6.6]
tf.reduce_max(data,axis=0)#按行求最大，结果为[5.5，6.6]
tf.reduce_mean(data,axis=1)#按列求平均，结果为[1.6500001，3.85，6.05]
tf.reduce_mean(data,axis=0)#按行求平均，结果为[3.3 4.4]
tf.reduce_sum(data,axis=1)#按列求和，结果为[3.3000002,7.7,12.1]
tf.reduce_sum(data,axis=0)#按行求和，结果为[9.9,13.200001]
data1=tf.constant(1,dtype=tf.float64)
data2=tf.constant(5,dtype=tf.float64)
data3=tf.constant([[1,2,3],[4,5,6],[7,8,9]],dtype=tf.int32)
tf.add(data1,data2)#加法，结果是6
tf.subtract(data1,data2)#减法，结果是-5
tf.multiply(data1,data2)#乘法，结果是5
tf.divide(data1,data2)#除法，结果是0.2
tf.square(data1)#平方，结果是1
tf.pow(data1,data2)#乘方，结果是1
tf.sqrt(data1)#开方，结果是1
tf.matmul(data3,data3)#矩阵乘法，结果如下：
#[[ 30  36  42], [ 66  81  96], [102 126 150]]
sess=tf.compat.v1.Session()#2.0版本没办法兼容Session。
A=tf.where(tf.greater(data1,data2),1,0)#data1是否比data2大？是则1，否则0
print(sess.run(A))#因为data1<data2所以是false，因此执行第二个赋值，A是0.
#输出为0
y1=tf.constant([0.1,0.6,0.3],dtype=tf.float32)
y_1=tf.constant([0.2,0.7,0.1],dtype=tf.float32)
B=tf.where(tf.greater(y1,y_1),1,0)#y1是否比y_1大？是则1，否则0
print(sess.run(B))#输出为[0 0 1]

三、Tensorflow网络框架基础函数用法

6、网络参数的初始化和可训练函数tf.Variable(张量)

函数的用法解释和说明：

tf.Variable(张量)将张量设置成为可训练的参数，在神经网络中可以进行训练和反向传播等操作。

example6：

w1=tf.Variable(tf.random.truncated_normal([2,35],mean=0,stddev=1))
b1=tf.Variable(tf.constant(0.01,shape=[35]))#2*35第一层
w2=tf.Variable(tf.random.truncated_normal([35,6],mean=0,stddev=1))
b2=tf.Variable(tf.constant(0.01,shape=[6]))#35*6第二层
w3=tf.Variable(tf.random.truncated_normal([66,1],mean=0,stddev=1))
b3=tf.Variable(tf.constant(0.01,shape=[1]))#6*1第三层

这里笔者定义了一个三层的神经网络参数，假定我们的输入是二维向量，为1×2的，第一层是2×35个参数，偏置为1×35，第一层走过之后为1×35的向量，现在走第二层，第二层是35×6个参数，偏置为1×6，第二层走过后为1×6的向量，我们假定输出为1个值，那么第三层为6×1个参数，偏置为1×1，这样输出就是1×1个值。在这里我们定义了6个可训练变量，可以在今后的反向传播和其他操作中使用这六个变量。

7、损失函数&激活函数

首先介绍softmax函数：

tf.nn.softmax(X)#将输入的N维向量X按照概率分布$p_i$输出如下：

$$p_i=\frac{e^{(x_i)}}{{\sum }_{j=1}^N{e}^{(x_j)}}$$

Ⅰ、损失函数loss(y1,y_1)，我们假设真实值为y1,网络输出值为y_1

①平方损失函数tf.reduce.mean(tf.square(y_1-y1))

②交叉熵损失函数tf.losses.categorical_crossentropy(y_1,y1)

交叉熵损失函数重点用法：送入交叉熵函数的y1和y_1比如都是概率分布！
所以一般先通过softmax将它化成概率分布后再进行交叉熵计算,交叉熵计算方法如下：H(y_1,y1)=$?\sum$(y_1)log(y1)

③不需要softmax直接可以计算的交叉熵损失函数，相当于softmax和交叉熵的合体版本：tf.nn.softmax_cross_entropy_with_logits(y_1,y）

example7：

y1=tf.constant([0.1,0.6,0.3],dtype=tf.float32)
y_1=tf.constant([0.2,0.7,0.1],dtype=tf.float32)
y2=tf.constant([1,6,3],dtype=tf.float32)
y_2=tf.constant([2,9,4],dtype=tf.float32)
tf.losses.categorical_crossentropy(y_1,y1)#交叉熵损失，结果为0.938
tf.reduce_mean(tf.square(y_1-y1))#平方损失，结果为0.020000001
tf.nn.softmax_cross_entropy_with_logits(y_2,y2)#直接计算交叉熵损失，结果为22.82478（不需要softmax了）

④自定义损失函数：例如以下分段函数：

loss(y1,y_1)=0.3(y_1-y1)(y_1>y1)
loss(y1,y_1)=0.5(y1-y_1)(y_1<y1)
则这里的定义方法有所不同，代码如下：

example8：自定义损失函数loss：

loss=tf.reduce_sum(tf.where(tf.greater(y_1,y1),0.3(y_1-y1),0.5(y1-y_1)))
print(sess.run(loss))#结果为0.16，请自行计算验证正确性

Ⅱ、激活函数

一般来说，如过网络上一层输入是$x$的话，不加任何激活，这一层的输出$y$应该是如下所示的：其中$w$为权重矩阵，$b$为偏置向量。
$$y=?x^{T}w+b$$
但是这样，是一个线性方程，而我们的神经网络目的是去模拟非线性的居多，因此需要增加非线性因素进来，如何增加非线性因素呢？这就引入了激活函数的出现。
激活函数改进点在于将原来的输出不再是线性的而是增加了非线性因素：
$$y=f(?x^{T}w+b)$$
这里的$f$我们称之为激活函数，上式也是正向传播的关键。激活函数有以下几个大类：

①sigmod：$f(x)=\frac{1}{1+e^x}$容易梯度消失

②tanh：$f(x)=\frac{1?e^{?2x}}{1+e^{?2x}}$容易梯度消失

③Relu：$f(x)=0(x<0),x(x\ge 0)$解决了大于零的梯度消失但是没解决小于零的，收敛速度慢

④Leaky Relu：$f(x)=max(ax,x)$$a$是超参数，一般由我们自己去给定，这个可以解决小于零的梯度消失问题，但是这个函数用的很少。

⑤其他的自定义激活函数

激活函数的好坏实际上也决定了网络搭建的好坏程度，因此，我们激活函数选取较好，网络效果和准确率也就越高，反之，如果你觉得你的网络训练的不好可以从激活函数下手，也可以从后面的网络优化入手来进行调整。

8、经典BP网络梯度的计算和tf.GradientTape()的梯度用法

这里mooc给出了一种利用with…as结构的梯度计算方式，大家参考一下，它有点类似一种简单省略版的try…except语句，详细用法本人不在这里赘述。

函数的用法解释和说明：

with tf.GradientTape() as tp:
     #这里面写网络的正向传播公式。
     #写完网络的正向传播公式之后，写网络的损失函数loss的定义
grades=tp.gradient(loss,待求偏导的参数列表)#求出梯度 

我们知道，在传统BP神经网络中，最经典的就是反向传播了，反向传播需要学习率和梯度来更新我们之前所设置的$w$权重矩阵和$b$偏置向量。也即给定了某个学习率$LR$后，梯度更新规则为(以$w$和$b$举例)：
$$w^{?}=w?LR\times grade{s}_w(grade{s}_w为w的梯度)$$
$$b^{?}=b?LR\times grade{s}_b(grade{s}_b为b的梯度)$$
在这里有些读者看完这个结构肯定会非常疑惑，不知道这是干什么的，怎么去用。但是没关系，我们先留下一个悬念，记住这个形式和反向传播的办法以及明白这个函数是求梯度的就可以了，我在后面给出完整的BP网络模型。我会为大家进行解释。

9、网络训练前对数据特征处理和参数选择。

下面这两个原则比较重要，大家一定要记住了，我们假设待训练的特征为N个。即需要输入到网络的特征数为N

①初始化网络的参数$\alpha$要满足以下正态分布：

$$\alpha ～N(0,\sqrt{\frac{2}{N}})$$

②输入的特征需要中心化，服从以下正态分布：

$$N(0,1)$$

10、特征，标签合并和喂入网络的batch选取函数

tf.data.Dataset.from_tensor_slices(输入特征，输出标签).batch($2^n$)

函数的用法解释和说明：

batch代表喂入神经网络训练的基本单位，通常为2的n次幂，n为自己给定，比如取2的5次幂32，那么就以32个为一组喂入神经网络进行训练，这个函数是将特征和标签进行整体打包并为神经网络后续函数调用做铺垫的，换而言之，这是一个合并函数。

11、其他重要的函数：

①enumerate枚举函数，用在for循环里面不仅可以得到元素值，而且还可以获得元素的对应位置，一举两得，不用在写繁琐的for函数了：

example9：

list1=[34,35,36]
for location,value in enumerate(list1):
    print(location,value)#location返回位置，value返回对应位置的值
#结果为0 34，1 35，2 36.

②变量.assign_sub(自减内容）

example10：

a=1
a.assign_sub(2)#相当于a变成了1-2=-1,这句话就是a=a-2
a.assign_sub(-2)#相当于a变成了1-(-2)=3这句话就是a=a-(-2)

③numpy下的np.mgrid[起始值:结束值:步长],.ravel(),np.c_[数组1，数组2]

example11：

import numpy as np
a=np.mgrid[-3:3:1]#a=[-3 -2 -1  0  1  2]
[a,b]=np.mgrid[-3:3:1,-5:5:1]
a.ravel()#拉直a成为一列
b.ravel()#拉直b成为一列
K=np.c_[a.ravel(),b.ravel()]#换成坐标点

四、最基础的神经网络TensorFlow构建

有了我们上述描述的内容和知识，我们可以开始着手搭建我们的第一个神经网络。本实例文件利用了mooc提供的dot.csv文件。以下我将分步骤进行讲解。

step1:import相关的库函数

我们需要pandas进行csv文件的读取，需要numpy对读取的数据进行预处理，需要tensorflow进行网络的构建，当然最好有图片画出来更完美了，因此我们需要这四个库进行调用。

import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd

step2:读取相关特征标签，并进行初设置网络内容。

以下是我用的数据集，它有两个特征x1和x2，他有一个输出y_c，因此我们选择的时候首先根据9，初始化网络参数时候他们都应该服从$N(0,1)$正态分布，大家可以自行选择数据集进行训练或者上我给的mooc官网下载dot数据集

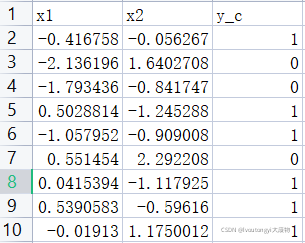
file=pd.read_csv('C:/Users/DELL/Desktop/dot.csv')#读取文件信息
x_data=np.array(file[['x1','x2']])#把file中名为这两列挑出来
y_data=np.array(file['y_c'])#把file中名为y_c的挑出来
x_train=np.vstack(x_data).reshape(-1,2)#垂直堆叠，并且转化成两列
y_train=np.vstack(y_data).reshape(-1,1)#垂直堆叠，并且转化成一列
#这里np.vstack函数代表垂直堆叠的意思
#reshape(-1,2)代表转化成两列（因为两个特征）
x_train=tf.cast(x_train,tf.float32)#转换数据类型为tf对象类型
y_train=tf.cast(y_train,tf.float32)#转换数据类型为tf对象类型
data=tf.data.Dataset.from_tensor_slices((x_train,y_train)).batch(32)
#32一组喂入神经网络，合并成总数据集
Ir=0.005#设置网络的学习率
epoch=3000#设置网络的训练轮数

step3:搭建网络框架

笔者这里选取了三层神经网络框架，相信看完了之前笔记部分，大家对我怎么搭建的有所了解了，看不懂的见example6。

w1=tf.Variable(tf.random.normal([2,35]),dtype=tf.float32)
b1=tf.Variable(tf.constant(0.01,shape=[35]))#1*35第一层输出
w2=tf.Variable(tf.random.normal([35,7]),dtype=tf.float32)#35*7第二层
b2=tf.Variable(tf.constant(0.01,shape=[7]))#1*7第二层输出
w3=tf.Variable(tf.random.normal([7,1]),dtype=tf.float32)#7*1第三层
b3=tf.Variable(tf.constant(0.01,shape=[1]))#1*1第三层输出

step4：正向传播和反向传播更新参数

相信大家已经记住了那个结构了吧，那么应该很容的能看懂这些都在干什么了：

for epoch in range(epoch):#训练3000轮
    for i,(x_train,y_train) in enumerate(data):#进行data的迭代
        with tf.GradientTape() as tape:#以下先进行正向传播
            h1=tf.matmul(x_train,w1)+b1#wx+b
            h1=tf.nn.relu(h1)#激活
            h2=tf.matmul(h1,w2)+b2#wx+b
            h2=tf.nn.relu(h2)#激活
            y=tf.matmul(h2,w3)+b3#wx+b
            #正向传播结束
            loss=tf.reduce_mean(tf.square(y_train-y))#定义损失函数
        variables=[w1,b1,w2,b2,w3,b3]#设置待求梯度的参数都有哪些
        grads=tape.gradient(loss,variables)#loss对每个变量求梯度
        w1.assign_sub(Ir*grads[0])#以下是参数更新过程，反向传播
        b1.assign_sub(Ir*grads[1])
        w2.assign_sub(Ir*grads[2])
        b2.assign_sub(Ir*grads[3])
        w3.assign_sub(Ir*grads[4])
        b3.assign_sub(Ir*grads[5])#六个参数都更新完，结束
   if(epoch%20==0):#每迭代20轮输出以下loss有多大
        print(epoch,float(loss))

step5：验证网络的好坏并进行测试对比

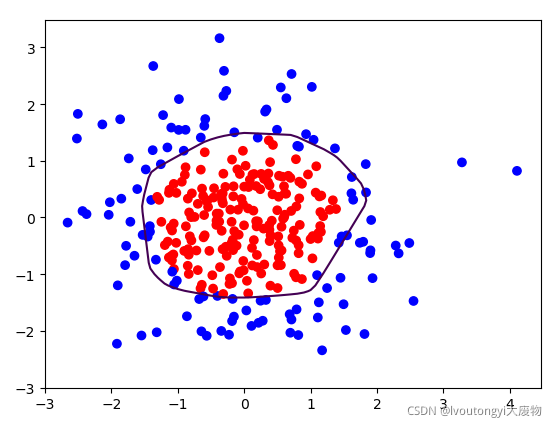
这样我们已经构建完了网络，但是不知道网络的好坏，我们首先需要画出我们的训练集散点图，这里我们要给两种颜色：

Y_c=[['red' if y else 'blue'] for y in y_train]#将0-1换成颜色列表
#如果y_train里面是1，那么赋值成'red'，否则赋值成'blue'
x1=x_data[:,0]#第一个坐标
x2=x_data[:,1]#第二个坐标
plt.scatter(x1,x2,color=np.squeeze(Y_c))#画出它的图像

结果如下所示
下面我们自己创造一些x1和x2作为测试数据来看看网络的训练效果

xx,yy=np.mgrid[-3:3:0.1,-3:3:0.1]
#设置网格点，步长是0.1，对应的为x1和x2
grid=np.c_[xx.ravel(),yy.ravel()]
#ravel是扁平化函数，将他们扁平化。
#np.c将它转化成网格坐标点，xx.ravel()为横坐标，yy.ravel()为纵坐标
grid=tf.cast(grid,tf.float32)#数据转换，便于进行计算
probs=[]#存储输出的y
for x_test in grid:#代入到训练好的网络中去
    h1=tf.matmul([x_test],w1)+b1
    h1=tf.nn.relu(h1)
    h2=tf.matmul(h1,w2)+b2
    h2=tf.nn.relu(h2)
    y=tf.matmul(h2,w3)+b3
    probs.append(y)#加入到数组中
probs=np.array(probs).reshape(xx.shape)#转化成和xx形状一样，便于画图
plt.contour(xx,yy,probs,levels=[0.5])
plt.scatter(x1,x2,color=np.squeeze(Y_c))#画出它的图像
plt.show()

以下是效果图：

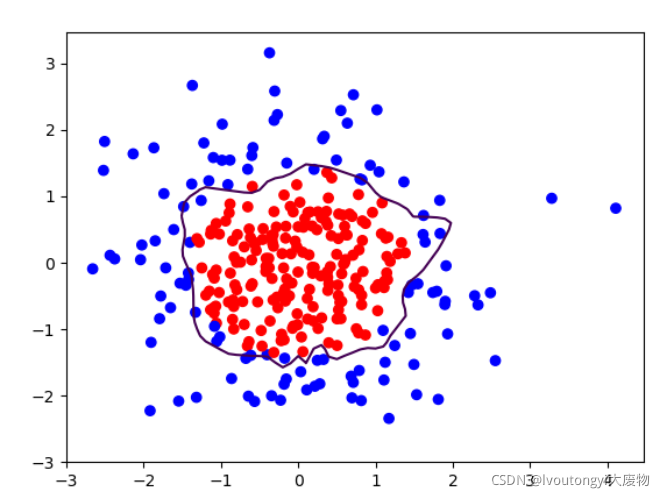
很明显的看出来了，这里面存在了过拟合现象！也就是这个曲线不平稳，这也就是我们现在要说的模型优化问题了。
这样我们将上面的代码合并起来，就得到了完整的网络结构和源代码，如下所示：

example12：

import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
file=pd.read_csv('C:/Users/DELL/Desktop/dot.csv')#读取文件信息存储成csv文件
x_data=np.array(file[['x1','x2']])#把file中名为这两列挑出来
y_data=np.array(file['y_c'])#把file中名为y_c的挑出来
x_train=np.vstack(x_data).reshape(-1,2)#转化成两列合并
y_train=np.vstack(y_data).reshape(-1,1)#转化成一列合并
Y_c=[['red' if y else 'blue'] for y in y_train]#将0-1换成颜色列表
x_train=tf.cast(x_train,tf.float32)#转换数据类型
y_train=tf.cast(y_train,tf.float32)#转换数据类型
data=tf.data.Dataset.from_tensor_slices((x_train,y_train)).batch(32)#32一组喂入神经网络，合并成总数据集
w1=tf.Variable(tf.random.normal([2,35]),dtype=tf.float32)
b1=tf.Variable(tf.constant(0.01,shape=[35]))#2*35第一层输出
w2=tf.Variable(tf.random.normal([35,7]),dtype=tf.float32)#35*36第二层
b2=tf.Variable(tf.constant(0.01,shape=[7]))#2*36第二层输出
w3=tf.Variable(tf.random.normal([7,1]),dtype=tf.float32)#36*1第三层
b3=tf.Variable(tf.constant(0.01,shape=[1]))
Ir=0.005#学习率
epoch=2000#训练轮数
for epoch in range(epoch):
    for i,(x_train,y_train) in enumerate(data):
        with tf.GradientTape() as tape:
            h1=tf.matmul(x_train,w1)+b1
            h1=tf.nn.relu(h1)
            h2=tf.matmul(h1,w2)+b2
            h2=tf.nn.relu(h2)
            y=tf.matmul(h2,w3)+b3
            """
            loss_regular=[]#加入网络正则化L2正则化
            loss_regular.append(tf.nn.l2_loss(w1))
            loss_regular.append(tf.nn.l2_loss(w2))
            loss_regular.append(tf.nn.l2_loss(w3))
            sum_loss=tf.reduce_sum(loss_regular)
            +0.03*sum_loss#计算误差(正则化后把它加在loss后面去)
            """
            loss=tf.reduce_mean(tf.square(y_train-y))
        variables=[w1,b1,w2,b2,w3,b3]
        grads=tape.gradient(loss,variables)
        w1.assign_sub(Ir*grads[0])
        b1.assign_sub(Ir*grads[1])
        w2.assign_sub(Ir*grads[2])
        b2.assign_sub(Ir*grads[3])
        w3.assign_sub(Ir*grads[4])
        b3.assign_sub(Ir*grads[5])
    if(epoch%20==0):
        print(epoch,float(loss))
xx,yy=np.mgrid[-3:3:0.1,-3:3:0.1];
print(xx,yy)
grid=np.c_[xx.ravel(),yy.ravel()]
grid=tf.cast(grid,tf.float32)
probs=[]
for x_test in grid:
    h1=tf.matmul([x_test],w1)+b1
    h1=tf.nn.relu(h1)
    h2=tf.matmul(h1,w2)+b2
    h2=tf.nn.relu(h2)
    y=tf.matmul(h2,w3)+b3
    probs.append(y)
x1=x_data[:,0]
x2=x_data[:,1]
probs=np.array(probs).reshape(xx.shape)
plt.scatter(x1,x2,color=np.squeeze(Y_c))
plt.contour(xx,yy,probs,levels=[0.5])
plt.show()

中间绿色注释掉的暂时不要看，在接下来的正则化部分中介绍它的作用。

五、网络动态学习率&网络正则化

通过上面我们发现了，网络存在着明显的过拟合现象，也就是虽然误差比较小，但是网络并不满足我们的要求，因此我们现在需要对网络进行优化，以下是笔者总结的比较重要的网络优化方法，便于大家对自己的网络进行改进

优化方法一：动态学习率

我们都知道，之前的学习率$LR$是给定的，那么这个给定的数值会影响网络的效果，我们不能把学习率给的太大，同时又不能给的太小，如果太大，则很容易越过梯度为0的点，如果太小，则收敛太慢甚至需要轮数太大，因此，我们可以采用动态学习率来进行改进这一缺点，定义动态学习率如下：
$$L{R}_m=LR?{\beta }^{\frac{当前轮数}{多少轮衰减一次}}(\beta 为给定的学习率衰减率)$$
比如我们定义如下，我们定义$\beta$为0.8，设置初始学习率为0.9，定义2轮训练学习率就衰减一次，则第$K$轮的学习率为：
$$L{R}_m=0.9\times 0.8^{\frac{K}{2}}$$
这样学习率会随着轮数的增加，越来越小，这就是动态学习率的意义，在程序中，将$LR$随着动态改变

优化方法二：正则化操作

针对网络的过拟合，往往可以采用增加正则化参数，提高网络数据集样本数量，采用网络正则化的办法来缓解过拟合问题，下面介绍两种正则化办法，相关两种正则化的原理和理论请参考其他博客，这里直接介绍。
我们一般正则化网络中的$w$,而很少正则化网络中的$b$
正则化即更改原来的损失函数，增加正则化损失即可。

①L1正则化

$$loss(w)=\sum _j|w_j|$$

②L2正则化

$$loss(w)=\sum _j|w_j^2|$$
更改后的$los{s}^{?}$为：
$$los{s}^{?}=loss+\gamma loss(w)。$$
其中$\gamma$为正则化权重，自行给定。
下面我们在example12的基础上增加网络的正则化代码，即加入这几行代码就可以了，就是注释的部分（笔者采用L2正则化操作)

loss_regular=[]#加入网络正则化L2正则化
loss_regular.append(tf.nn.l2_loss(w1))#w1的l2正则化
loss_regular.append(tf.nn.l2_loss(w2))#w2的l2正则化
loss_regular.append(tf.nn.l2_loss(w3))#w3的l2正则化
sum_loss=tf.reduce_sum(loss_regular)#计算总的正则化loss
loss=tf.reduce_mean(tf.square(y_train-y))+0.03*sum_loss
#正则化权重0.03

再加入网络的动态学习率变化：

Irbase=0.01#基础学习率
Ir=Irbase*(0.99**(epoch/1))#一轮迭代一次

但是改进的动态学习率不宜过高，因为轮数过大，会使得后者趋于0，那么这个时候学习率就是0了！那就不会再有参数更新的过程了，因此不宜取过大的epoch轮数。
下图是加入网络的正则化后，网络的训练效果，可以明显地看到，过拟合有一定的缓解了，曲线变得平缓了,正则化得到了缓解，如下图所示，大家可以自己试一下

六、网络动量优化