GTSAM Tutorial学习笔记

为了学习LIO-SAM，我快速过了一遍《机器人感知：因子图在SLAM中的应用》以及董靖大佬在泡泡机器人分享的《GTSAM Tutorial》，本博客内容主要是《GTSAM Tutorial》的学习笔记，并对GTSAM在LIO-SAM中的实际应用进行一些简单分析，如果对GTSAM有基本了解的同学可以直接跳到第三部分。

1. 基本原理

在下图是一个典型SLAM场景
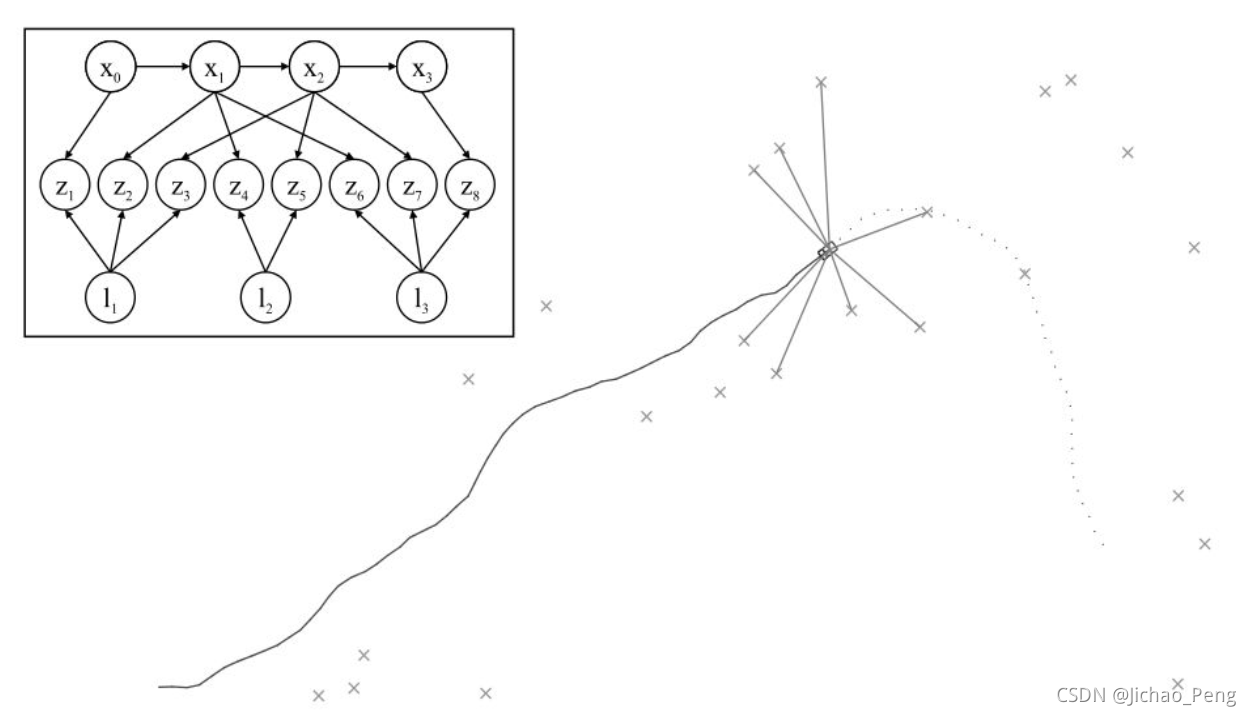
在这里插入图片描述
其中，机器人对特征点的观测可以构建为如上左图所示的一个贝叶斯网络，该贝叶斯网络中 $x_i$ 为机器人状态， $z_i$ 为机器人观测值， $l_i$ 为特征点。这样一个贝叶斯网络的联合分布概率可以通过如下公式表示： $Z)=P\left(x_{0}\right) \prod_{i=1}^{M} P\left(x_{i} \mid x_{i-1}, u_{i}\right) \prod_{k=1}^{K} P\left(z_{k} \mid x_{i_{k}}, l_{j_{k}}\right)$ 其中，
$P\left(x_{0}\right)$ 为先验状态概率分布，
$P\left(x_{i} \mid x_{i-1}, u_{i}\right)$ 表示已知状态 $x_{i-1}$ 和控制量 $u_{i}$ 分布的情况下， $\boldsymbol{x}_{i}$ 的概率分布，具体为： $x_{i}=f_{i}\left(x_{i-1}, u_{i}\right)+w_{i} \quad \Leftrightarrow$ $P\left(x_{i} \mid x_{i-1}, u_{i}\right) \propto \exp -\frac{1}{2}\left\|f_{i}\left(x_{i-1}, u_{i}\right)-x_{i}\right\|_{\Lambda_{i}}^{2}$ $P\left(z_{k} \mid x_{i_{k}}, l_{j_{k}}\right)$ 标示已知状态 $\boldsymbol{x}_{i_{k}}$ 和 $l_{j_{k}}$ 的分布的情况下， $z_{k}$ 的概率分布，具体为： $z_{k}=h_{k}\left(x_{i_{k}}, l_{j_{k}}\right)+v_{k} \quad \Leftrightarrow$ $P\left(z_{k} \mid x_{i_{k}}, l_{j_{k}}\right) \propto \exp -\frac{1}{2}\left\|h_{k}\left(x_{i_{k}}, l_{j_{k}}\right)-z_{k}\right\|_{\Sigma_{k}}^{2}$ 如果将以上分布都假定为高斯分布，那么就可以构建如下因子图：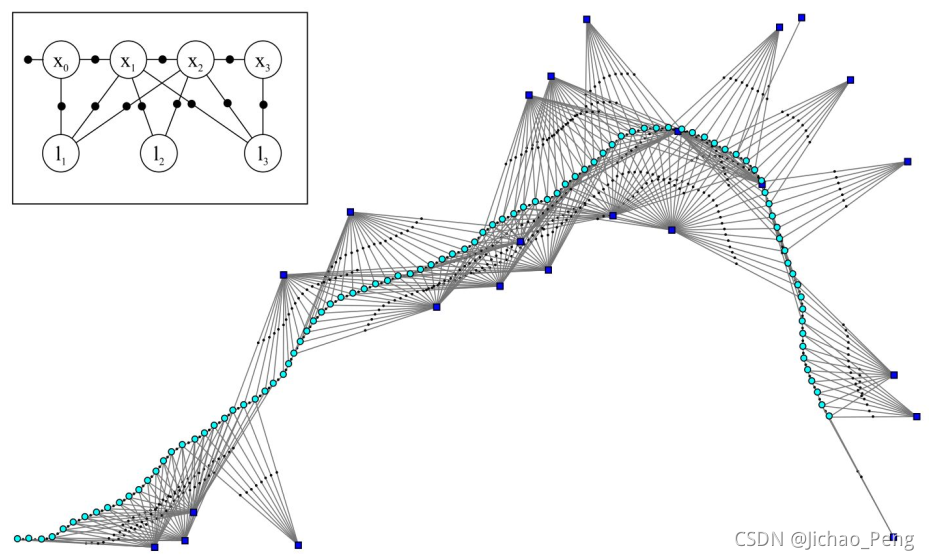在这里插入图片描述
我们通过如下公式表示以上因子图： $P(\Theta) \propto \prod_{i} \phi_{i}\left(\theta_{i}\right) \prod_{\{i, j\}, i<j} \psi_{i j}\left(\theta_{i}, \theta_{j}\right)，\Theta \triangleq(X, L)$ 其中 $\phi_{0}\left(x_{0}\right) \propto P\left(x_{0}\right)$ $\psi_{(i-1) i}\left(x_{i-1}, x_{i}\right) \propto P\left(x_{i} \mid x_{i-1}, u_{i}\right)$ $\psi_{i_{k} j_{k}}\left(x_{i_{k}}, l_{j_{k}}\right) \propto P\left(z_{k} \mid x_{i_{k}}, l_{j_{k}}\right)$ 这样，我们相当于将机器人状态和周围的地图点都等同于因子图中的一个因子，整个因子图的后验概率其实就可以建模是所有因子之间的后验概率的乘积： $f(\Theta)=\prod_{i} f_{i}\left(\Theta_{i}\right) \quad \Theta \triangleq(X, L) \quad \text { for each } f_{i}\left(\Theta_{i}\right) \propto \exp \left(-\frac{1}{2}\left\|h_{i}\left(\Theta_{i}\right)-z_{i}\right\|_{\Sigma_{i}}^{2}\right)$ 而我们的目标就是让总的后验概率最大： $\Theta^{*增量优化：}=\underset{\Theta}{\arg \max } f(\Theta)$ 直观理解就是我们求解什么样的机器人状态和地图点分布可以让当前的所有观测发生的概率最大，因为是高斯概率分布，因此我们通常将概率分布转到对数域： $\underset{\Theta}{\arg \min }(-\log f(\Theta))=\underset{\Theta}{\arg \min } \frac{1}{2} \sum_{i}\left\|h_{i}\left(\Theta_{i}\right)-z_{i}\right\|_{\Sigma_{i}}^{2}$ 求解该问题主要就是通过非线性优化算法，例如高斯牛顿法或者列文伯格法，那么整个求解过程如下在这里插入图片描述
这里还有几点需要注意：

增量优化：以上介绍的都是对于一个固定Batch数据的求解方法，而实际的SLAM问题是一个增量问题，在基于后端优化的方法增量优化：中，通常是采用滑窗的方式来进行局部地图优化，而在GTSAM中，是通过iSAM2构建的Bayers Tree来实现增量优化，如下图所示，红色区域表示GTSAM进行优化的区域，GTSAM只会取当前状态临近的状态和地图点进行优化，而对于即使产生回环，也只会在回环区域周围进行优化，这一部分细节在《iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree》。
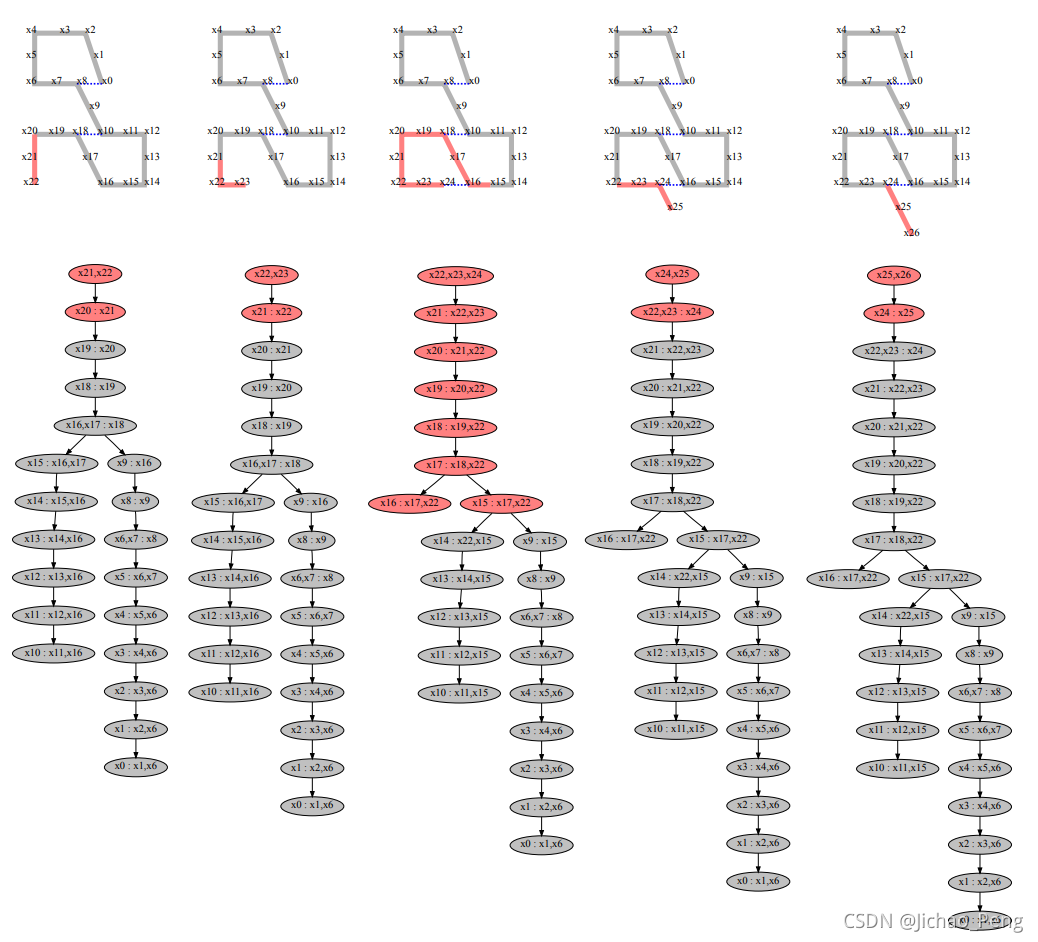
自动排序：我们知道不管是在高斯牛顿法还是列文伯格法中，都有一个重要步骤就是求解 $A X = b$ ，求解该矩阵通常有QR分解和Cholesky分解两种方法，其中QR分解如下： $Q^{T} A=\left[\begin{array}{l} R \\ 0 \end{array}\right] \quad Q^{T} b=\left[\begin{array}{l} d \\ e \end{array}\right]$ $\delta=d$ Cholesky分解如下： $A^{T} A \delta^{*}=A^{T} b$ $\mathcal{I} \triangleq A^{T} A=R^{T} R$ $\text { first } R^{T} y=A^{T} b \text { and then } R \delta^{*}=y$ Cholesky分解效率在某些情况下相对QR分解要高一个数量级，但是Cholesky分解在矩阵近似奇异时稳定性不如QR分解，但是不管是那种分解方法，分解效率都很大情况下取决于矩阵的稀疏性，在GTSAM中通过COLAMD算法使得我们A矩阵尽可能稀疏，从而提高计算效率。

2. Demo代码

在《GTSAM Tutorial》提供的Demo代码中，描述了如何构造如下图一个带回环的因子图
在这里插入图片描述
首先构建一个因子图容器

  // Create a factor graph container
  NonlinearFactorGraph graph;

接下来构建和添加先验因子，也就是图中的蓝色因子部分，注意该因子为一元边

  // prior measurment noise model 
  noiseModel::Diagonal::shared_ptr priorModel = noiseModel::Diagonal::Sigmas(Vector3(1.0, 1.0, 0.1));
  
  // Add a prior on the first pose, setting it to the origin
  // The prior is needed to fix/align the whole trajectory at world frame
  // A prior factor consists of a mean value and a noise model (covariance matrix)
  graph.add(PriorFactor<Pose2>(Symbol('x', 1), Pose2(0, 0, 0), priorModel));

然后是构建和添加里程计因子，也就是图中的黑色因子部分，这些因子为二元边

  // odometry measurement noise model (covariance matrix)
  noiseModel::Diagonal::shared_ptr odomModel = noiseModel::Diagonal::Sigmas(Vector3(0.5, 0.5, 0.1));

  // Add odometry factors
  // Create odometry (Between) factors between consecutive poses
  // robot makes 90 deg right turns at x3 - x5
  graph.add(BetweenFactor<Pose2>(Symbol('x', 1), Symbol('x', 2), Pose2(5, 0, 0), odomModel));
  graph.add(BetweenFactor<Pose2>(Symbol('x', 2), Symbol('x', 3), Pose2(5, 0, -M_PI_2), odomModel));
  graph.add(BetweenFactor<Pose2>(Symbol('x', 3), Symbol('x', 4), Pose2(5, 0, -M_PI_2), odomModel));
  graph.add(BetweenFactor<Pose2>(Symbol('x', 4), Symbol('x', 5), Pose2(5, 0, -M_PI_2), odomModel));

还有回环因子，也就是途中的红色因子部分，该因子为二元边

  // loop closure measurement noise model
  noiseModel::Diagonal::shared_ptr loopModel = noiseModel::Diagonal::Sigmas(Vector3(0.5, 0.5, 0.1));

  // Add the loop closure constraint
  graph.add(BetweenFactor<Pose2>(Symbol('x', 5), Symbol('x', 2), Pose2(5, 0, -M_PI_2), loopModel));

从上面可以看到，添加因子的过程就是先构造噪声模型，然后将因子类型，因子连接的节点，以及初始值添加到因子图的容器中，接下来就是初始化各个节点的噪声模型

  // initial varible values for the optimization
  // add random noise from ground truth values
  Values initials;
  initials.insert(Symbol('x', 1), Pose2(0.2, -0.3, 0.2));
  initials.insert(Symbol('x', 2), Pose2(5.1, 0.3, -0.1));
  initials.insert(Symbol('x', 3), Pose2(9.9, -0.1, -M_PI_2 - 0.2));
  initials.insert(Symbol('x', 4), Pose2(10.2, -5.0, -M_PI + 0.1));
  initials.insert(Symbol('x', 5), Pose2(5.1, -5.1, M_PI_2 - 0.1));

最后就是构建优化器以及执行优化

  // Use Gauss-Newton method optimizes the initial values
  GaussNewtonParams parameters;
  
  // print per iteration
  parameters.setVerbosity("ERROR");
  
  // optimize!
  GaussNewtonOptimizer optimizer(graph, initials, parameters);
  Values results = optimizer.optimize();

通过Marginals类可以获得各个节点优化后的残差值

  // Calculate marginal covariances for all poses
  Marginals marginals(graph, results);
  
  // print marginal covariances
  cout << "x1 covariance:\n" << marginals.marginalCovariance(Symbol('x', 1)) << endl;
  cout << "x2 covariance:\n" << marginals.marginalCovariance(Symbol('x', 2)) << endl;
  cout << "x3 covariance:\n" << marginals.marginalCovariance(Symbol('x', 3)) << endl;
  cout << "x4 covariance:\n" << marginals.marginalCovariance(Symbol('x', 4)) << endl;
  cout << "x5 covariance:\n" << marginals.marginalCovariance(Symbol('x', 5)) << endl;

以上就是Demo代码中的核心部分，可以看出来，GTSAM构建因子图的过程是非常简单明了的，接下来我们看看GTSAM在实际的工程中是怎么应用的。

3. LIO-SAM中部分代码分析

LIO-SAM中构建的因子图如下：
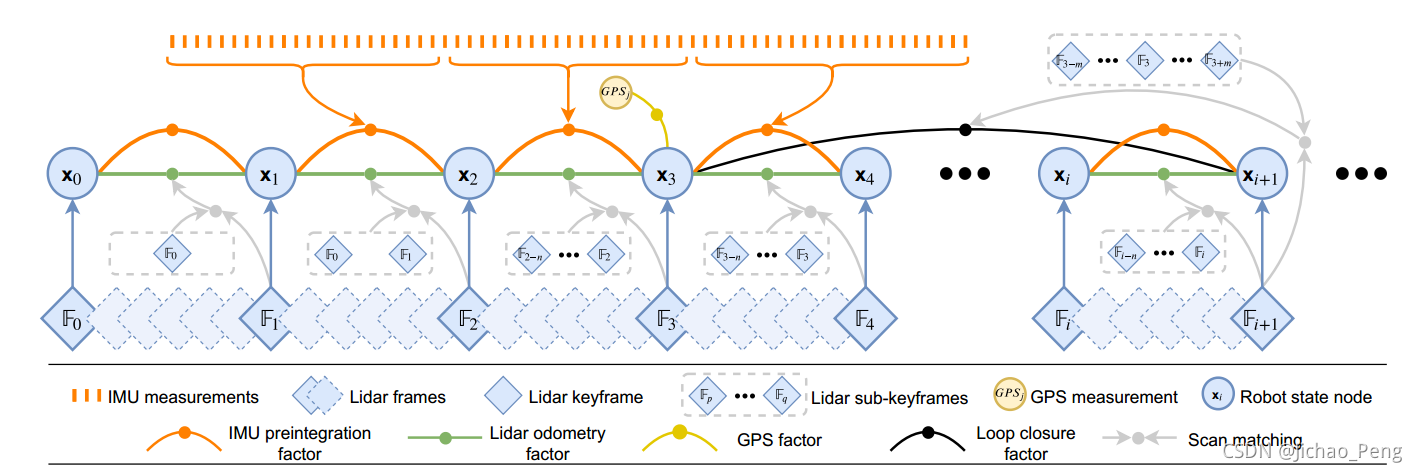
在这里插入图片描述
上图看上去是一个因子图，但是在LIO-SAM中实际上一共有两种类型的因子图，第一种因子图是在imuIntergration.cpp文件中，用激光里程计，两帧激光里程计之间的IMU预积分量构建因子图，优化当前帧的状态（包括位姿、速度、偏置），这里我们称之为预积分因子图。第二种因子图是在mapOptimization.cpp文件中，关键帧加入因子图，添加激光里程计因子、GPS因子、闭环因子，执行因子图优化，更新所有关键帧位姿，这里我们成为关键帧因子图。下面具体来看（部分代码注释参考LIO-SAM源码解析）：

3.1 预积分因子图

预积分因子图相关代码主要在imuIntergration.cpp的IMUPreintegration类中，该类定义如下：

class IMUPreintegration : public ParamServer
{
public:
    std::mutex mtx;

	// 订阅与发布
	ros::Subscriber subImu;
	ros::Subscriber subOdometry;
	ros::Publisher pubImuOdometry;
	
	bool systemInitialized = false;
	
	// 噪声协方差
	gtsam::noiseModel::Diagonal::shared_ptr priorPoseNoise;
	gtsam::noiseModel::Diagonal::shared_ptr priorVelNoise;
	gtsam::noiseModel::Diagonal::shared_ptr priorBiasNoise;
	gtsam::noiseModel::Diagonal::shared_ptr correctionNoise;
	gtsam::noiseModel::Diagonal::shared_ptr correctionNoise2;
	gtsam::Vector noiseModelBetweenBias;
	
	// imu预积分器
	gtsam::PreintegratedImuMeasurements *imuIntegratorOpt_;
	gtsam::PreintegratedImuMeasurements *imuIntegratorImu_;
	
	// imu数据队列
	std::deque<sensor_msgs::Imu> imuQueOpt;
	std::deque<sensor_msgs::Imu> imuQueImu;
	
	// imu因子图优化过程中的状态变量
	gtsam::Pose3 prevPose_;
	gtsam::Vector3 prevVel_;
	gtsam::NavState prevState_;
	gtsam::imuBias::ConstantBias prevBias_;
	
	// imu状态
	gtsam::NavState prevStateOdom;
	gtsam::imuBias::ConstantBias prevBiasOdom;
	
	bool doneFirstOpt = false;
	double lastImuT_imu = -1;
	double lastImuT_opt = -1;
	
	// ISAM2优化器
	gtsam::ISAM2 optimizer;
	gtsam::NonlinearFactorGraph graphFactors;
	gtsam::Values graphValues;
	
	const double delta_t = 0;
	
	// 用于记录第几个关键帧
	int key = 1;
	
	// imu-lidar位姿变换
	gtsam::Pose3 imu2Lidar = gtsam::Pose3(gtsam::Rot3(1, 0, 0, 0), gtsam::Point3(-extTrans.x(), -extTrans.y(), -extTrans.z()));
	gtsam::Pose3 lidar2Imu = gtsam::Pose3(gtsam::Rot3(1, 0, 0, 0), gtsam::Point3(extTrans.x(), extTrans.y(), extTrans.z()));

	// 构造函数
    IMUPreintegration();

	// 重置iSAM2优化器
    void resetOptimization();

	// 重置参数
    void resetParams();

	// 订阅激光里程计
    void odometryHandler(const nav_msgs::Odometry::ConstPtr& odomMsg);

	// IMU因子图优化结果判定
    bool failureDetection(const gtsam::Vector3& velCur, const gtsam::imuBias::ConstantBias& biasCur);

	// 订阅原始IMU数据
    void imuHandler(const sensor_msgs::Imu::ConstPtr& imu_raw);
};

其中类的成员变量包括需要优化的各个状态，以及各个先验因子的噪声协方差，这些参数都在构造函数中初始化，下面我们看构造函数内容：

IMUPreintegration()
{
    // 订阅imu原始数据，用下面因子图优化的结果，施加两帧之间的imu预计分量，预测每一时刻（imu频率）的imu里程计
    subImu      = nh.subscribe<sensor_msgs::Imu>  (imuTopic,                   2000, &IMUPreintegration::imuHandler,      this, ros::TransportHints().tcpNoDelay());
    // 订阅激光里程计，来自mapOptimization，用两帧之间的imu预计分量构建因子图，优化当前帧位姿（这个位姿仅用于更新每时刻的imu里程计，以及下一次因子图优化）
    subOdometry = nh.subscribe<nav_msgs::Odometry>("lio_sam/mapping/odometry_incremental", 5,    &IMUPreintegration::odometryHandler, this, ros::TransportHints().tcpNoDelay());
    
    // 发布imu里程计
    pubImuOdometry = nh.advertise<nav_msgs::Odometry> (odomTopic+"_incremental", 2000);

    // imu预积分的噪声协方差
    boost::shared_ptr<gtsam::PreintegrationParams> p = gtsam::PreintegrationParams::MakeSharedU(imuGravity);
    p->accelerometerCovariance  = gtsam::Matrix33::Identity(3,3) * pow(imuAccNoise, 2); // acc white noise in continuous
    p->gyroscopeCovariance      = gtsam::Matrix33::Identity(3,3) * pow(imuGyrNoise, 2); // gyro white noise in continuous
    p->integrationCovariance    = gtsam::Matrix33::Identity(3,3) * pow(1e-4, 2); // error committed in integrating position from velocities
    gtsam::imuBias::ConstantBias prior_imu_bias((gtsam::Vector(6) << 0, 0, 0, 0, 0, 0).finished());; // assume zero initial bias

    // 噪声先验
    priorPoseNoise  = gtsam::noiseModel::Diagonal::Sigmas((gtsam::Vector(6) << 1e-2, 1e-2, 1e-2, 1e-2, 1e-2, 1e-2).finished()); // rad,rad,rad,m, m, m
    priorVelNoise   = gtsam::noiseModel::Isotropic::Sigma(3, 1e4); // m/s
    priorBiasNoise  = gtsam::noiseModel::Isotropic::Sigma(6, 1e-3); // 1e-2 ~ 1e-3 seems to be good
    // 激光里程计scan-to-map优化过程中发生退化，则选择一个较大的协方差
    correctionNoise = gtsam::noiseModel::Diagonal::Sigmas((gtsam::Vector(6) << 0.05, 0.05, 0.05, 0.1, 0.1, 0.1).finished()); // rad,rad,rad,m, m, m
    correctionNoise2 = gtsam::noiseModel::Diagonal::Sigmas((gtsam::Vector(6) << 1, 1, 1, 1, 1, 1).finished()); // rad,rad,rad,m, m, m
    noiseModelBetweenBias = (gtsam::Vector(6) << imuAccBiasN, imuAccBiasN, imuAccBiasN, imuGyrBiasN, imuGyrBiasN, imuGyrBiasN).finished();
    
    // imu预积分器，用于预测每一时刻（imu频率）的imu里程计（转到lidar系了，与激光里程计同一个系）
    imuIntegratorImu_ = new gtsam::PreintegratedImuMeasurements(p, prior_imu_bias); // setting up the IMU integration for IMU message thread
    // imu预积分器，用于因子图优化
    imuIntegratorOpt_ = new gtsam::PreintegratedImuMeasurements(p, prior_imu_bias); // setting up the IMU integration for optimization        
}

接下来构建因子图最核心的部分就在订阅激光里程计函数函数中，具体如下:

/**
 * 订阅激光里程计，来自mapOptimization
 * 1、每隔100帧激光里程计，重置ISAM2优化器，添加里程计、速度、偏置先验因子，执行优化
 * 2、计算前一帧激光里程计与当前帧激光里程计之间的imu预积分量，用前一帧状态施加预积分量得到当前帧初始状态估计，添加来自mapOptimization的当前帧位姿，进行因子图优化，更新当前帧状态
 * 3、优化之后，执行重传播；优化更新了imu的偏置，用最新的偏置重新计算当前激光里程计时刻之后的imu预积分，这个预积分用于计算每时刻位姿
*/
void odometryHandler(const nav_msgs::Odometry::ConstPtr& odomMsg)
{
    std::lock_guard<std::mutex> lock(mtx);
    // 当前帧激光里程计时间戳
    double currentCorrectionTime = ROS_TIME(odomMsg);

    // 确保imu优化队列中有imu数据进行预积分
    if (imuQueOpt.empty())
        return;

    // 当前帧激光位姿，来自scan-to-map匹配、因子图优化后的位姿
    float p_x = odomMsg->pose.pose.position.x;
    float p_y = odomMsg->pose.pose.position.y;
    float p_z = odomMsg->pose.pose.position.z;
    float r_x = odomMsg->pose.pose.orientation.x;
    float r_y = odomMsg->pose.pose.orientation.y;
    float r_z = odomMsg->pose.pose.orientation.z;
    float r_w = odomMsg->pose.pose.orientation.w;
    bool degenerate = (int)odomMsg->pose.covariance[0] == 1 ? true : false;
    gtsam::Pose3 lidarPose = gtsam::Pose3(gtsam::Rot3::Quaternion(r_w, r_x, r_y, r_z), gtsam::Point3(p_x, p_y, p_z));


    // 0. 系统初始化，第一帧
    if (systemInitialized == false)
    {
        // 重置ISAM2优化器
        resetOptimization();

        // 从imu优化队列中删除当前帧激光里程计时刻之前的imu数据
        while (!imuQueOpt.empty())
        {
            if (ROS_TIME(&imuQueOpt.front()) < currentCorrectionTime - delta_t)
            {
                lastImuT_opt = ROS_TIME(&imuQueOpt.front());
                imuQueOpt.pop_front();
            }
            else
                break;
        }
        // 添加里程计位姿先验因子
        prevPose_ = lidarPose.compose(lidar2Imu);
        gtsam::PriorFactor<gtsam::Pose3> priorPose(X(0), prevPose_, priorPoseNoise);
        graphFactors.add(priorPose);
        // 添加速度先验因子
        prevVel_ = gtsam::Vector3(0, 0, 0);
        gtsam::PriorFactor<gtsam::Vector3> priorVel(V(0), prevVel_, priorVelNoise);
        graphFactors.add(priorVel);
        // 添加imu偏置先验因子
        prevBias_ = gtsam::imuBias::ConstantBias();
        gtsam::PriorFactor<gtsam::imuBias::ConstantBias> priorBias(B(0), prevBias_, priorBiasNoise);
        graphFactors.add(priorBias);
        // 变量节点赋初值
        graphValues.insert(X(0), prevPose_);
        graphValues.insert(V(0), prevVel_);
        graphValues.insert(B(0), prevBias_);
        // 优化一次
        optimizer.update(graphFactors, graphValues);
        graphFactors.resize(0);
        graphValues.clear();
        
        // 重置优化之后的偏置
        imuIntegratorImu_->resetIntegrationAndSetBias(prevBias_);
        imuIntegratorOpt_->resetIntegrationAndSetBias(prevBias_);
        
        key = 1;
        systemInitialized = true;
        return;
    }


    // 每隔100帧激光里程计，重置ISAM2优化器，保证优化效率
    if (key == 100)
    {
        // 前一帧的位姿、速度、偏置噪声模型
        gtsam::noiseModel::Gaussian::shared_ptr updatedPoseNoise = gtsam::noiseModel::Gaussian::Covariance(optimizer.marginalCovariance(X(key-1)));
        gtsam::noiseModel::Gaussian::shared_ptr updatedVelNoise  = gtsam::noiseModel::Gaussian::Covariance(optimizer.marginalCovariance(V(key-1)));
        gtsam::noiseModel::Gaussian::shared_ptr updatedBiasNoise = gtsam::noiseModel::Gaussian::Covariance(optimizer.marginalCovariance(B(key-1)));
        // 重置ISAM2优化器
        resetOptimization();
        // 添加位姿先验因子，用前一帧的值初始化
        gtsam::PriorFactor<gtsam::Pose3> priorPose(X(0), prevPose_, updatedPoseNoise);
        graphFactors.add(priorPose);
        // 添加速度先验因子，用前一帧的值初始化
        gtsam::PriorFactor<gtsam::Vector3> priorVel(V(0), prevVel_, updatedVelNoise);
        graphFactors.add(priorVel);
        // 添加偏置先验因子，用前一帧的值初始化
        gtsam::PriorFactor<gtsam::imuBias::ConstantBias> priorBias(B(0), prevBias_, updatedBiasNoise);
        graphFactors.add(priorBias);
        // 变量节点赋初值，用前一帧的值初始化
        graphValues.insert(X(0), prevPose_);
        graphValues.insert(V(0), prevVel_);
        graphValues.insert(B(0), prevBias_);
        // 优化一次
        optimizer.update(graphFactors, graphValues);
        graphFactors.resize(0);
        graphValues.clear();

        key = 1;
    }


    // 1. 计算前一帧与当前帧之间的imu预积分量，用前一帧状态施加预积分量得到当前帧初始状态估计，添加来自mapOptimization的当前帧位姿，进行因子图优化，更新当前帧状态
    while (!imuQueOpt.empty())
    {
        // 提取前一帧与当前帧之间的imu数据，计算预积分
        sensor_msgs::Imu *thisImu = &imuQueOpt.front();
        double imuTime = ROS_TIME(thisImu);
        if (imuTime < currentCorrectionTime - delta_t)
        {
            // 两帧imu数据时间间隔
            double dt = (lastImuT_opt < 0) ? (1.0 / 500.0) : (imuTime - lastImuT_opt);
            // imu预积分数据输入：加速度、角速度、dt
            imuIntegratorOpt_->integrateMeasurement(
                    gtsam::Vector3(thisImu->linear_acceleration.x, thisImu->linear_acceleration.y, thisImu->linear_acceleration.z),
                    gtsam::Vector3(thisImu->angular_velocity.x,    thisImu->angular_velocity.y,    thisImu->angular_velocity.z), dt);
            
            lastImuT_opt = imuTime;
            // 从队列中删除已经处理的imu数据
            imuQueOpt.pop_front();
        }
        else
            break;
    }
    // 添加imu预积分因子
    const gtsam::PreintegratedImuMeasurements& preint_imu = dynamic_cast<const gtsam::PreintegratedImuMeasurements&>(*imuIntegratorOpt_);
    // 参数：前一帧位姿，前一帧速度，当前帧位姿，当前帧速度，前一帧偏置，预积分量
    gtsam::ImuFactor imu_factor(X(key - 1), V(key - 1), X(key), V(key), B(key - 1), preint_imu);
    graphFactors.add(imu_factor);
    // 添加imu偏置因子，前一帧偏置，当前帧偏置，观测值，噪声协方差；deltaTij()是积分段的时间
    graphFactors.add(gtsam::BetweenFactor<gtsam::imuBias::ConstantBias>(B(key - 1), B(key), gtsam::imuBias::ConstantBias(),
                        gtsam::noiseModel::Diagonal::Sigmas(sqrt(imuIntegratorOpt_->deltaTij()) * noiseModelBetweenBias)));
    // 添加位姿因子
    gtsam::Pose3 curPose = lidarPose.compose(lidar2Imu);
    gtsam::PriorFactor<gtsam::Pose3> pose_factor(X(key), curPose, degenerate ? correctionNoise2 : correctionNoise);
    graphFactors.add(pose_factor);
    // 用前一帧的状态、偏置，施加imu预计分量，得到当前帧的状态
    gtsam::NavState propState_ = imuIntegratorOpt_->predict(prevState_, prevBias_);
    // 变量节点赋初值
    graphValues.insert(X(key), propState_.pose());
    graphValues.insert(V(key), propState_.v());
    graphValues.insert(B(key), prevBias_);
    // 优化
    optimizer.update(graphFactors, graphValues);
    optimizer.update();
    graphFactors.resize(0);
    graphValues.clear();
    // 优化结果
    gtsam::Values result = optimizer.calculateEstimate();
    // 更新当前帧位姿、速度
    prevPose_  = result.at<gtsam::Pose3>(X(key));
    prevVel_   = result.at<gtsam::Vector3>(V(key));
    // 更新当前帧状态
    prevState_ = gtsam::NavState(prevPose_, prevVel_);
    // 更新当前帧imu偏置
    prevBias_  = result.at<gtsam::imuBias::ConstantBias>(B(key));
    // 重置预积分器，设置新的偏置，这样下一帧激光里程计进来的时候，预积分量就是两帧之间的增量
    imuIntegratorOpt_->resetIntegrationAndSetBias(prevBias_);

    // imu因子图优化结果，速度或者偏置过大，认为失败
    if (failureDetection(prevVel_, prevBias_))
    {
        // 重置参数
        resetParams();
        return;
    }


    // 2. 优化之后，执行重传播；优化更新了imu的偏置，用最新的偏置重新计算当前激光里程计时刻之后的imu预积分，这个预积分用于计算每时刻位姿
    prevStateOdom = prevState_;
    prevBiasOdom  = prevBias_;
    // 从imu队列中删除当前激光里程计时刻之前的imu数据
    double lastImuQT = -1;
    while (!imuQueImu.empty() && ROS_TIME(&imuQueImu.front()) < currentCorrectionTime - delta_t)
    {
        lastImuQT = ROS_TIME(&imuQueImu.front());
        imuQueImu.pop_front();
    }
    // 对剩余的imu数据计算预积分
    if (!imuQueImu.empty())
    {
        // 重置预积分器和最新的偏置
        imuIntegratorImu_->resetIntegrationAndSetBias(prevBiasOdom);
        // 计算预积分
        for (int i = 0; i < (int)imuQueImu.size(); ++i)
        {
            sensor_msgs::Imu *thisImu = &imuQueImu[i];
            double imuTime = ROS_TIME(thisImu);
            double dt = (lastImuQT < 0) ? (1.0 / 500.0) :(imuTime - lastImuQT);

            imuIntegratorImu_->integrateMeasurement(gtsam::Vector3(thisImu->linear_acceleration.x, thisImu->linear_acceleration.y, thisImu->linear_acceleration.z),
                                                    gtsam::Vector3(thisImu->angular_velocity.x,    thisImu->angular_velocity.y,    thisImu->angular_velocity.z), dt);
            lastImuQT = imuTime;
        }
    }

    ++key;
    doneFirstOpt = true;
}

其中较为特殊一点的就是gtsam::PreintegratedImuMeasurements类的使用，找个类相当于把一堆预积分及其雅克比推导公式都给封装起来了，简直不要太爽。从代码中我们也可以看出来，在构建因子图过程中稍微复杂一点的部分就是因子的Noise Model的给定过程。

3.2 关键帧因子图

关键帧因子图相关代码主要在mapOptimization.cpp的saveKeyFramesAndFactor函数中，在mapOptimization.cpp中除了关键帧因子图部分，还包括Scan-to-Map的匹配算法，关键帧判定等，对这些代码我们就不做过多介绍，saveKeyFramesAndFactor函数如下：

/**
 * 设置当前帧为关键帧并执行因子图优化
 * 1、计算当前帧与前一帧位姿变换，如果变化太小，不设为关键帧，反之设为关键帧
 * 2、添加激光里程计因子、GPS因子、闭环因子
 * 3、执行因子图优化
 * 4、得到当前帧优化后位姿，位姿协方差
 * 5、添加cloudKeyPoses3D，cloudKeyPoses6D，更新transformTobeMapped，添加当前关键帧的角点、平面点集合
*/
void saveKeyFramesAndFactor()
{
    // 计算当前帧与前一帧位姿变换，如果变化太小，不设为关键帧，反之设为关键帧
    if (saveFrame() == false)
        return;

    // 激光里程计因子
    addOdomFactor();

    // GPS因子
    addGPSFactor();

    // 闭环因子
    addLoopFactor();

    // cout << "****************************************************" << endl;
    // gtSAMgraph.print("GTSAM Graph:\n");
    
    // 执行优化
    isam->update(gtSAMgraph, initialEstimate);
    isam->update();

    if (aLoopIsClosed == true)
    {
        isam->update();
        isam->update();
        isam->update();
        isam->update();
        isam->update();
    }

    // update之后要清空一下保存的因子图，注：历史数据不会清掉，ISAM保存起来了
    gtSAMgraph.resize(0);
    initialEstimate.clear();

    PointType thisPose3D;
    PointTypePose thisPose6D;
    Pose3 latestEstimate;

    // 优化结果
    isamCurrentEstimate = isam->calculateEstimate();
    // 当前帧位姿结果
    latestEstimate = isamCurrentEstimate.at<Pose3>(isamCurrentEstimate.size()-1);
    // cout << "****************************************************" << endl;
    // isamCurrentEstimate.print("Current estimate: ");

    // cloudKeyPoses3D加入当前帧位姿
    thisPose3D.x = latestEstimate.translation().x();
    thisPose3D.y = latestEstimate.translation().y();
    thisPose3D.z = latestEstimate.translation().z();
    // 索引
    thisPose3D.intensity = cloudKeyPoses3D->size(); 
    cloudKeyPoses3D->push_back(thisPose3D);

    // cloudKeyPoses6D加入当前帧位姿
    thisPose6D.x = thisPose3D.x;
    thisPose6D.y = thisPose3D.y;
    thisPose6D.z = thisPose3D.z;
    thisPose6D.intensity = thisPose3D.intensity ; 
    thisPose6D.roll  = latestEstimate.rotation().roll();
    thisPose6D.pitch = latestEstimate.rotation().pitch();
    thisPose6D.yaw   = latestEstimate.rotation().yaw();
    thisPose6D.time = timeLaserInfoCur;
    cloudKeyPoses6D->push_back(thisPose6D);

    // cout << "****************************************************" << endl;
    // cout << "Pose covariance:" << endl;
    // cout << isam->marginalCovariance(isamCurrentEstimate.size()-1) << endl << endl;
    // 位姿协方差
    poseCovariance = isam->marginalCovariance(isamCurrentEstimate.size()-1);

    // transformTobeMapped更新当前帧位姿
    transformTobeMapped[0] = latestEstimate.rotation().roll();
    transformTobeMapped[1] = latestEstimate.rotation().pitch();
    transformTobeMapped[2] = latestEstimate.rotation().yaw();
    transformTobeMapped[3] = latestEstimate.translation().x();
    transformTobeMapped[4] = latestEstimate.translation().y();
    transformTobeMapped[5] = latestEstimate.translation().z();

    // 当前帧激光角点、平面点，降采样集合
    pcl::PointCloud<PointType>::Ptr thisCornerKeyFrame(new pcl::PointCloud<PointType>());
    pcl::PointCloud<PointType>::Ptr thisSurfKeyFrame(new pcl::PointCloud<PointType>());
    pcl::copyPointCloud(*laserCloudCornerLastDS,  *thisCornerKeyFrame);
    pcl::copyPointCloud(*laserCloudSurfLastDS,    *thisSurfKeyFrame);

    // 保存特征点降采样集合
    cornerCloudKeyFrames.push_back(thisCornerKeyFrame);
    surfCloudKeyFrames.push_back(thisSurfKeyFrame);

    // 更新里程计轨迹
    updatePath(thisPose6D);
}

历史上所有状态变量优化的结果保存在isamCurrentEstimate中，而最新帧的结果在latestEstimate中，其中添加里程计因子的函数为

void addOdomFactor()
{
    if (cloudKeyPoses3D->points.empty())
    {
        noiseModel::Diagonal::shared_ptr priorNoise = noiseModel::Diagonal::Variances((Vector(6) << 1e-2, 1e-2, M_PI*M_PI, 1e8, 1e8, 1e8).finished()); // rad*rad, meter*meter
        gtSAMgraph.add(PriorFactor<Pose3>(0, trans2gtsamPose(transformTobeMapped), priorNoise));
        initialEstimate.insert(0, trans2gtsamPose(transformTobeMapped));
    }else{
        noiseModel::Diagonal::shared_ptr odometryNoise = noiseModel::Diagonal::Variances((Vector(6) << 1e-6, 1e-6, 1e-6, 1e-4, 1e-4, 1e-4).finished());
        gtsam::Pose3 poseFrom = pclPointTogtsamPose3(cloudKeyPoses6D->points.back());
        gtsam::Pose3 poseTo   = trans2gtsamPose(transformTobeMapped);
        gtSAMgraph.add(BetweenFactor<Pose3>(cloudKeyPoses3D->size()-1, cloudKeyPoses3D->size(), poseFrom.between(poseTo), odometryNoise));
        initialEstimate.insert(cloudKeyPoses3D->size(), poseTo);
    }
}

添加GPS因子函数为，这个相对复杂些，需要判断是否加入以及插值：

void addGPSFactor()
{
    if (gpsQueue.empty())
        return;

    // wait for system initialized and settles down
    if (cloudKeyPoses3D->points.empty())
        return;
    else
    {
        if (pointDistance(cloudKeyPoses3D->front(), cloudKeyPoses3D->back()) < 5.0)
            return;
    }

    // pose covariance small, no need to correct
    if (poseCovariance(3,3) < poseCovThreshold && poseCovariance(4,4) < poseCovThreshold)
        return;

    // last gps position
    static PointType lastGPSPoint;

    while (!gpsQueue.empty())
    {
        if (gpsQueue.front().header.stamp.toSec() < timeLaserInfoCur - 0.2)
        {
            // message too old
            gpsQueue.pop_front();
        }
        else if (gpsQueue.front().header.stamp.toSec() > timeLaserInfoCur + 0.2)
        {
            // message too new
            break;
        }
        else
        {
            nav_msgs::Odometry thisGPS = gpsQueue.front();
            gpsQueue.pop_front();

            // GPS too noisy, skip
            float noise_x = thisGPS.pose.covariance[0];
            float noise_y = thisGPS.pose.covariance[7];
            float noise_z = thisGPS.pose.covariance[14];
            if (noise_x > gpsCovThreshold || noise_y > gpsCovThreshold)
                continue;

            float gps_x = thisGPS.pose.pose.position.x;
            float gps_y = thisGPS.pose.pose.position.y;
            float gps_z = thisGPS.pose.pose.position.z;
            if (!useGpsElevation)
            {
                gps_z = transformTobeMapped[5];
                noise_z = 0.01;
            }

            // GPS not properly initialized (0,0,0)
            if (abs(gps_x) < 1e-6 && abs(gps_y) < 1e-6)
                continue;

            // Add GPS every a few meters
            PointType curGPSPoint;
            curGPSPoint.x = gps_x;
            curGPSPoint.y = gps_y;
            curGPSPoint.z = gps_z;
            if (pointDistance(curGPSPoint, lastGPSPoint) < 5.0)
                continue;
            else
                lastGPSPoint = curGPSPoint;

            gtsam::Vector Vector3(3);
            Vector3 << max(noise_x, 1.0f), max(noise_y, 1.0f), max(noise_z, 1.0f);
            noiseModel::Diagonal::shared_ptr gps_noise = noiseModel::Diagonal::Variances(Vector3);
            gtsam::GPSFactor gps_factor(cloudKeyPoses3D->size(), gtsam::Point3(gps_x, gps_y, gps_z), gps_noise);
            gtSAMgraph.add(gps_factor);

            aLoopIsClosed = true;
            break;
        }
    }
}

添加回环因子函数如下所示：

void addLoopFactor()
{
    if (loopIndexQueue.empty())
        return;

    for (int i = 0; i < (int)loopIndexQueue.size(); ++i)
    {
        int indexFrom = loopIndexQueue[i].first;
        int indexTo = loopIndexQueue[i].second;
        gtsam::Pose3 poseBetween = loopPoseQueue[i];
        gtsam::noiseModel::Diagonal::shared_ptr noiseBetween = loopNoiseQueue[i];
        gtSAMgraph.add(BetweenFactor<Pose3>(indexFrom, indexTo, poseBetween, noiseBetween));
    }

    loopIndexQueue.clear();
    loopPoseQueue.clear();
    loopNoiseQueue.clear();
    aLoopIsClosed = true;
}