开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 决策树原理 -> 正文阅读

[人工智能]决策树原理

前言

决策树原理：ID3算法，c4.5算法，CART算法

一、决策树是什么？

决策树（Decision Tree）是一种非参数的有监督学习方法，它能够从一系列有特征和标签的数据中总结出决策规则，并用树状图的结构来呈现这些规则，以解决分类和回归问题。

最初的问题所在的地方叫做根节点，在得到结论前的每一个问题都是中间节点，而得到的每一个结论（动物的类别）都叫做叶子节点。

决策树算法的核心是要解决两个问题：
1）如何从数据表中找出最佳节点和最佳分枝
2）如何让决策树停止生长，防止过拟合

二、算法原理

ID3算法

1.ID3算法概述

为了要将表格转化为一棵树，决策树需要找出最佳节点和最佳的分枝方法，而衡量这个“最佳”的指标叫做“不纯度”。不纯度基于叶子节点计算，所以树中的每个节点都会有一个不纯度，并且子节点的不纯度一定是低于父节点的，也就是说，在同一棵决策树上，叶子节点的不纯度一定是最低的。

什么是不纯度
决策树的每个叶子节点中都会包含一组数据，在这组数据中，如果有某一类标签占有较大的比例，我们就说叶子节点“纯”，分枝分得好。某一类标签占的比例越大，叶子就越纯，不纯度就越低，分枝就越好。如果没有哪一类标签的比例很大，各类标签都相对平均，则说叶子节点”不纯“，分枝不好，不纯度高。

分类型决策树在叶子节点上的决策规则是少数服从多数，在一个叶子节点上，如果某一类标
签所占的比例较大，那所有进入这个叶子节点的样本都会被认为是这一类别。

不纯度越低，决策树对训练集的拟合越好。

2.计算不纯度的方法

误差率

对于节点不纯度的计算和表示方法因决策树模型而异，但不管不纯度的度量方法如何，都是由误差率衍生而来，其计算公式如下：
$Classification-error(t)=1-\max_{i=1} [p(i|t)]$
误差率越低，则纯度越高
信息熵

信息熵，又叫做香农熵，其计算公式如下：
$Entropy(t)=-\sum_{i=0}^{c-1} p(i|t)\log_2 p(i|t)$
其中 $c$ 表示叶子节点上标签类别的个数， $c ? 1$ 表示标签的索引。注意在这里，是从第0类标签开始计算，所以最后的标签类别应该是总共c个标签，c-1为最后一个标签的索引。在计算Entropy时设定 $log_20=0$ 。
Gini(基尼系数)

主要用于CART决策树的纯度判定中，其计算公式如下：
$Gini=1-\sum_{i=0}^{c-1} [p(i|t)]^2$

3.公式应用及总结特征

假设在二分类问题中各节点呈现如下分布，则可进一步计算上述三指数的结果
在这里插入图片描述
能够看出，三种方法本质上都相同，在类分布均衡时（即当p=0.5时）达到最大值，而当所有记录都属于同一个类时（p等于1或0）达到最小值。换而言之，在纯度较高时三个指数均较低，而当纯度较低时，三个指数都比较大，且可以计算得出，熵在0-1区间内分布，而Gini指数和分类误差均在0-0.5区间内分布，三个指数随某变量占比增加而变化的曲线如下所示：
在这里插入图片描述
决策树最终的优化目标是使得叶节点的总不纯度最低，即对应衡量不纯度的指标最低。

ID3最优条件是叶节点的总信息熵最小，因此ID3决策树在决定是否对某节点进行切分的时候，会尽可能选取使得该节点对应的子节点信息熵最小的特征进行切分。换而言之，就是要求父节点信息熵和子节点总信息熵之差要最大。对于ID3而言，二者之差就是信息增益。

注意
一个父节点下可能有多个子节点，而每个子节点又有自己的信息熵，所以父节点信息熵和子节点信
息熵之差，应该是父节点的信息熵 - 所有子节点信息熵的加权平均。其中，权重是使用单个叶子节点上所占的样本量比上父节点上的总样本量来确定的一个权重，公式如下：
$I(child)=\sum_{j=1}^{k} \frac{N(v_j)}{N} I(v_j)$
而父节点和子节点的不纯度下降数可由下述公式进行计算：
$\Delta=I(parent)-I(child)$
I(.)是给定结点的不纯性度量（即是基尼系数或者信息熵），N是父结点上的样本数，k是这一层上子节点的个数， $N(v_j)$ 是与子结点 $v_j$ 相关联的样本个数。决策树算法通常选择最大化增益的测试条件，因为对任何分枝过程来说，I(parent)都是一个不变的值（因为此时父节点已经存在并且不可修改），所以最大化增益等价于最小化子结点的不纯性衡量的加权平均。最后，当选择熵（entropy）作为公式的不纯性度量时，熵的差就是所谓信息增益（Information gain） info。

4. 举例说明

假设现在有如下数据集，是一个消费者个人属性和信用评分数据，标签是”是否会发生购买电脑行为“，仍然是个而分类问题，在此数据集之上我们使用ID3构建决策树模型，并提取有效的分类规则。
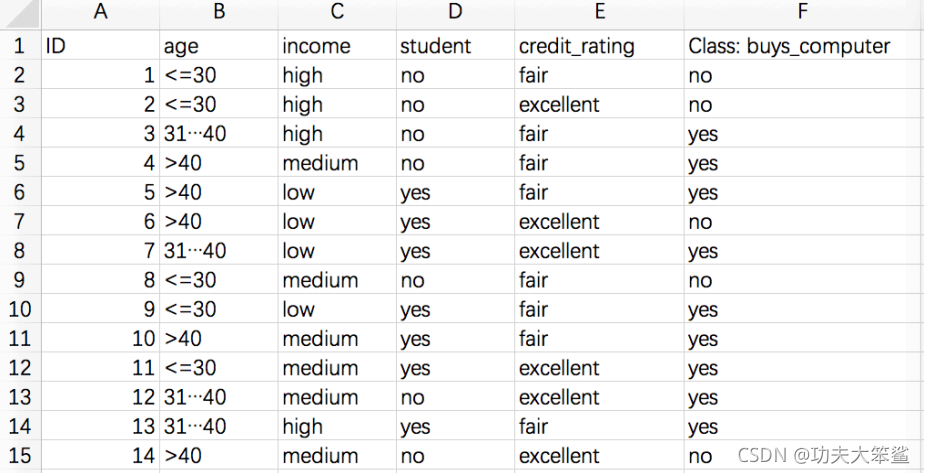
在这里插入图片描述
首先计算原始数据集的信息熵，我们可设置树模型中每个节点信息熵的表示方法，首先对于根节点而言，信息熵可用 $I(s_1,s_2)$ 来表示，其中s下标1和2代表两个分类水平， $s_1$ 和 $s_2$ 则代表分类水平下的对应样本个数，其计算公式如下所示：
$Entropy(t)=-\sum_{i=0}^{c-1} p(i|t)\log_2 p(i|t)$
对于根节点（购买电脑的行为）5个no，9个yes
$I(s_1,s_2)=I(9,5)=-\frac{9}{14} \log_2 \frac{9}{14}-\frac{5}{14} \log_2 \frac{5}{14}=0.940$
即在不进行任何切分前，总信息熵为0.940。然后我们依次选取各特征来尝试进行切分，并计算切分完成后的子节点信息熵是多少。首先选取age列进行切分，age是三分类的离散变量，因此若用age对根节点进行切分，将有三个分支，每个分支分别对应一个age的取值，分支所指向的子节点为对应的切分后的数据集

计算子节点的信息熵:
当 $a g e < = 30 :$
$s_{11}=2$ ???? $s_{21}=3$ ???? $I(s_{11},s_{21})=-\frac{2}{5} \log_2\frac{2}{5}-\frac{3}{5} \log_2\frac{3}{5}=0.971$
当 $a g e = 31 . . . . . 40 :$
$s_{12}=4$ ???? $s_{22}=0$ ???? $I(s_{12},s_{22})=-\frac{4}{4} \log_2\frac{4}{4}-0 \log_20=0$
当 $a g e > 40 :$
$s_{13}=3$ ???? $s_{23}=2$ ???? $I(s_{13},s_{23})=-\frac{3}{5} \log_2\frac{3}{5}-\frac{2}{5} \log_2\frac{2}{5}=0.971$

$E(age)=\frac{5}{15}I(s_{11},s_{21})+\frac{4}{15}I(s_{12},s_{22})+\frac{5}{15}I(s_{13},s_{23})=0.694$

即对于age属性而言，在根节点上切分一次之后子节点的信息熵为0.694，由此我们可计算age的信息增益，即局部最优化判别指标：
$Gain(age)=I(s_1,s_2)-E(age)=0.246$
以此类推，我们还能计算其他几个特征的信息增益，最终计算结果如下
Gain(income) = 0.029，Gain(student) = 0.15，Gain(credit_rating) = 0.048，很明显，第一次切分过程将采用age字段进行切分：

$a g e < = 30$ 数据集：

ID	age	income	student	credit_rating	Class: buys_computer
1	<=30	high	no	fair	no
2	<=30	high	no	excellent	no
8	<=30	medium	no	fair	no
9	<=30	low	yes	fair	yes
11	<=30	medium	yes	excellent	yes

$a g e = 31 . . . 40$ 数据集：

ID	age	income	student	credit_rating	Class: buys_computer
3	31…40	high	no	fair	yes
7	31…40	low	yes	excellent	yes
12	31…40	medium	no	excellent	yes
13	31…40	high	yes	fair	yes

$a g e > 40$ 数据集：

ID	age	income	student	credit_rating	Class: buys_computer
4	>40	medium	no	fair	yes
5	>40	low	yes	fair	yes
6	>40	low	yes	excellent	no
10	>40	medium	yes	fair	yes
14	>40	medium	no	excellent	no

第一次切分完成后，分成了三个数据集，其中age=“31…40"分类指标所指向的数据集纯度为1，因此不用再进行切分，而其他两个数据集则需要进一步进行切分，对于age="<=30"的数据集而言使用student特征进行切分后子节点纯度就将为1，而age=">40"的数据集则可采用credit_rating字段进行切分。
当credit_rating为fair时，buys_computer都为yes，因此纯度为1
当credit_rating为excellent时，buys_computer都为no，因此纯度为1
最终ID3决策树模型如下所示：
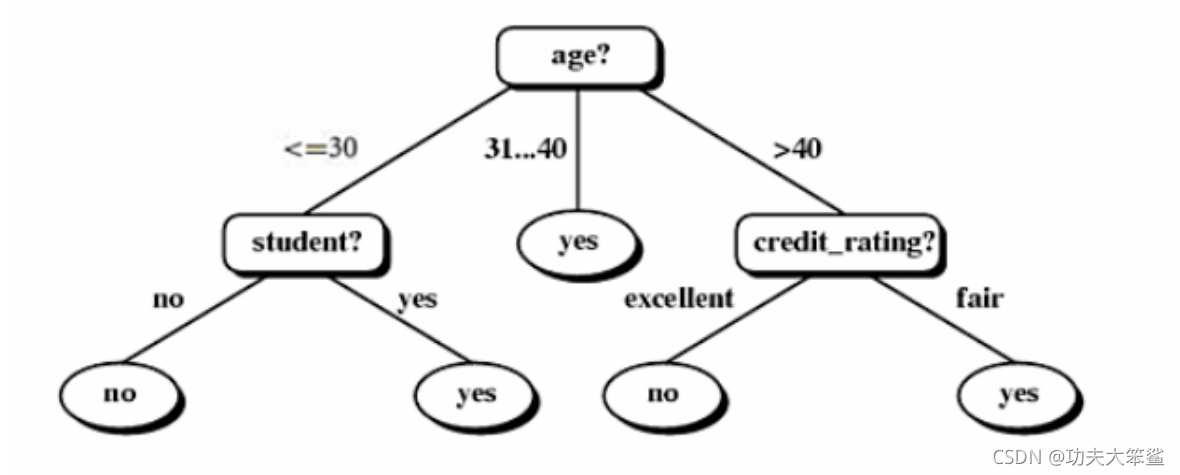
在这里插入图片描述

5.总结

总的来说，决策树模型是一个典型的贪心模型，总目标是一个全局最优解，即一整套合理的分类规则使得最终叶节点的纯度最高，但全局最优解在随特征增加而呈现指数级增加的搜索空间内很难高效获取，因此我们退而求其次，考虑采用局部最优来一步步推导结果——只要保证信息增益最大，我们就能得到次最优的模型。

6. ID3的局限性

ID3局限主要源于局部最优化条件，即信息增益的计算方法，其局限性主要有以下几点：

分支度越高（分类水平越多）的离散变量往往子节点的总信息熵会更小，ID3是按照某一列进行切分，有一些列的分类可能不会对我需要的结果有足够好的指示。极限情况下取ID作为切分字段，每个分类的纯度都是100%，因此这样的分类方式是没有效益的。
不能直接处理连续型变量，若要使用ID3处理连续型变量，则首先需要对连续变量进行离散化
对缺失值较为敏感，使用ID3之前需要提前对缺失值进行处理
没有剪枝的设置，容易导致过拟合，即在训练集上表现很好，测试集上表现很差

过拟合与欠拟合
过拟合：模型在训练集上表现很好，在测试集上表现很糟糕，学习能力很强但是学得太过精细了
欠拟合：模型在训练集和测试集上都表现糟糕，学习能力不足

C4.5算法

在决策树算法中，最经典，最常用的是C4.5算法，它在决策树算法中的主要优点是形象直观

1. C4.5与ID3和CART的区别

C4.5是基于ID3优化的算法，ID3基于信息增益进行分支，C4.5基于信息增益率进行分支（多了个随着属性取值数量增多而变大的分母），CART基于基尼系数。
ID3只能处理离散的分类的变量，对缺失值敏感；C4.5可以处理离散的、连续的变量，对缺失值有多种处理方法，但是C4.5处理过程需要对数据进行排序，耗时成本高，适用于小样本；CART同样可以处理连续和分类两种变量，也处理缺失值，适用于大样本。
ID3和C4.5只能做分类，CART可以做分类和回归
ID3和C4.5都只能在树中用一次变量，CART可以多次使用
C4.5有剪枝修正，CART利用利用全部数据对比树的结构来取舍

2. 修改局部最优化的条件

在信息增益计算方法的子节点总信息熵的计算方法中添加了随着分类变量水平的惩罚项。而分支度的计算公式仍然是基于熵的算法，只是将信息熵计算公式中的 $p (i ∣ t)$ (即某类别样例占总样例数)改成了 $p(v_i)$ ，即某子节点的总样本数占父节点总样本数的比例，这其实就是我们加权求和时的”权重“。这样的一个分支度指标，让我们在切分的时候，自动避免那些分类水平太多，信息熵减小过快的特征影响模型，减少过拟合情况。IV计算公式如下：
$Information-Value=-\sum_{i=1}^{k} p(v_i)\log_2 p(v_i)$
其中， $i$ 表示父节点的第 $i$ 个子节点， $v_i$ 表示第 $i$ 个子节点样例数， $p(v_i)$ 表示第 $i$ 个子节点拥有样例数占父节点总样例数的比例。很明显，IV可作为惩罚项带入子节点的信息熵计算中。可以简单计算得出，当取ID字段作为切分字段时，IV值为 $log_2k$ 。所以IV值会随着叶子节点上样本量的变小而逐渐变大，这就是说一个特征中如果标签分类太多，每个叶子上的IV值就会非常大。

在C4.5中，使用之前的信息增益除以分支度作为选取切分字段的参考指标，该指标被称作Gain Rati（增益率），计算公式如下：
$Gain-Ratio=\frac{Information-Gain}{Information-Value}$
增益比例是我们决定对哪一列进行分枝的标准，我们分枝的是数字最大的那一列，本质是信息增益最大，分支度又较小的列（也就是纯度提升很快，但又不是靠着把类别分特别细来提升的那些特征）。IV越大，即某一列的分类水平越多，Gain ratio实现的惩罚比例越大。当然，我们还是希望GR越大越好。

3. 利用GR重新计算上面的例子

计算age字段的GR，由于根据age字段切分后，3个分支分别有5个、4个和5个样例数据，因此age的IV指标计算过程如下：
$IV(age)=-\frac{5}{14}\log_2\frac{5}{14}-\frac{4}{14}\log_2\frac{4}{14}-\frac{5}{14}\log_2\frac{5}{14}=1.577$
进而可计算age列的GR：
$GR(age)=\frac{Gain(age)}{IV(age)}=\frac{0.246}{1.577}=0.156$
然后可进一步计算其他各字段的GR值，并选取GR值最大的字段进行切分。

4. 连续变量处理手段

在C4.5中，同样还增加了针对连续变量的处理手段。如果输入特征字段是连续型变量，则有下列步骤：

算法首先会对这一列数进行从小到大的排序
选取相邻的两个数的中间数作为切分数据集的备选点，若一个连续变量有N个值，则在C4.5的处理过程中将产生N-1个备选切分点，并且每个切分点都代表着一种二叉树的切分方案，此时针对连续变量的处理并非是将其转化为一个拥有N-1个分类水平的分类变量，而是将其转化成了N-1个二分方案，而在进行下一次的切分过程中，这N-1个方案都要单独带入考虑，其中每一个切分方案和一个
离散变量的地位均相同（一个离散变量就是一个单独的多路切分方案）。

例如：
有如下数据集，数据集中只有两个字段，第一行代表年龄，是特征变量，第二行代表性别，是目标字段，则对年龄这一连续变量的切分方案如图所示：
在这里插入图片描述
对于包含连续变量的数据集进行树模型构建的过程中要消耗更多的运算资源
当连续变量的某中间点参与到决策树的二分过程中，往往代表该点对于最终分类结果有较大影响，这也为我们连续变量的分箱压缩提供了指导性意见，若要对age列进行压缩，则可考虑使用36.5对其进行分箱，则分箱结果对于性别这一目标字段仍然具有较好的分类效果，这也是决策树的最常见用途之一，也是最重要的模型指导分箱的方法

CART算法

CART树是由C4.5改进而来，CART树本质其实和C4.5区别不大，只不过CART树所有的层都是二叉树，也就是每层只有两个分枝。

对于上述例子，假设年龄是特征，性别是标签：

首先将年龄从小到大依此进行排列
然后计算俩俩相邻的年龄的均值
按均值所在的点，对连续性变量进行二分（变成数字形式的，第一类是>均值，第二类是<均值），二分得到的
点叫做决策树的“ 树桩”。这是说，对于一个含有n个记录的连续性变量来说，就会存在n-1个潜在切分点，这n-1个潜在切分点的获益比例都都会被计算
找每种二分切分方案的获益比例，获益比例最大的切分点，就是切点
切完之后，计算加权信息熵，计算信息增益，引入分支度，可以计算出增益比例了

需要注意的是，这种切分方法，每次切分之后，并没有消费掉一列，只消费掉了一个备选点。在我们原本的切分方法中，ID3每次切分就会消费掉一整个列，但实际上，我们可以只关注每次分类的时候，对信息熵的减少贡献最多的那个分类。
按照上面的例子：分类age的时候，最关注的是31-40岁的那一个分类，我们完全可以实现，31-40一类，其他算一类，然后我们再对“其他”这个类别进行相似的二分类。这就是CART的核心原理，大量地减少了计算的量。