[人工智能]图像处理与傅里叶变换

图像处理与傅里叶变换

一维傅里叶变换

• 连续域

$$F(w)={\int }_{?\infty }^{\infty }f(x)e^{?j2\pi wx}dx$$

$$f(x)={\int }_{?\infty }^{\infty }F(w)e^{j2\pi wx}dw$$

• 离散域

$$F(k)=\frac{1}{N}\sum _{x=0}^{N?1}f(x)e^{?j2\pi kx/N},k=0,1,2,...N?1$$

$$f(x)=\sum _{k=0}^{N?1}F(k)e^{j2\pi kx/N},x=0,1,2,...N?1$$

二维傅里叶变换

• 连续域

$$F(u,v)={\int }_{?\infty }^{\infty }{\int }_{?\infty }^{\infty }f(x,y)e^{?2j\pi (xu+yv)}dxdy$$

$$f(x,y)={\int }_{?\infty }^{\infty }{\int }_{?\infty }^{\infty }F(u,v)e^{2j\pi (xu+yv)}dudv$$

• 离散域

$$F(u,v)=\frac{1}{MN}\sum _{x=0}^{N?1}\sum _{y=0}^{M?1}f(x,y)e^{?2j\pi [\frac{xu}{N}+\frac{yv}{M}]}$$

$$f(x,y)=\sum _{x=0}^{N?1}\sum _{y=0}^{M?1}F(u,v)e^{2j\pi [\frac{xu}{N}+\frac{yv}{M}]}$$

$$\begin{gathered} x=0,1,2,...N?1,y=0,1,2,...M?1 \\ u=0,1,2,...N?1,v=0,1,2,...M?1 \end{gathered}$$

# -*- coding: utf-8 -*-
"""
Created on Sun Oct 10 16:05:40 2021
@author: shiyi
"""

import numpy as np
import matplotlib.pyplot as plt

PI = np.pi
N = 256

x = np.linspace(0, 1, N)
y = np.linspace(0, 1, N)
X,Y = np.meshgrid(x, y) 

wx = 10 * PI
wy = 0 * PI
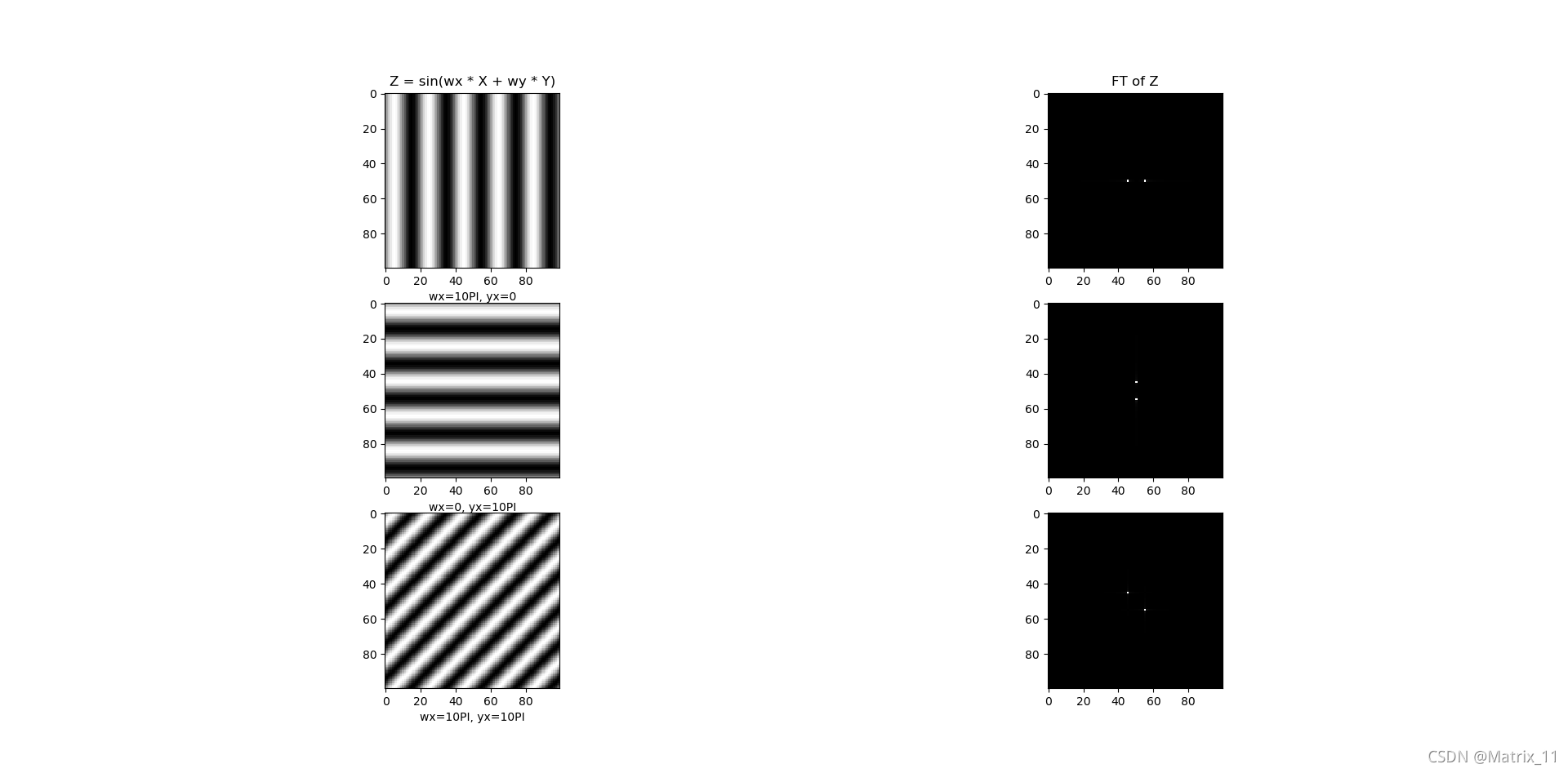
Z = np.sin(wx * X + wy * Y)
fft_ = np.fft.fft2(Z)
fshift_ = np.fft.fftshift(fft_) 
mag_fft = (np.abs(fshift_))
plt.figure(figsize=(10, 8))
plt.subplot(3, 2, 1)
plt.imshow(Z, cmap='gray')
plt.xlabel('wx=10PI, yx=0')
plt.title('Z = sin(wx * X + wy * Y)')
plt.subplot(3, 2, 2)
plt.imshow(mag_fft, cmap='gray')
plt.title('FT of Z')


wx = 0 * PI
wy = 10 * PI
Z = np.sin(wx * X + wy * Y)
fft_ = np.fft.fft2(Z)
fshift_ = np.fft.fftshift(fft_) 
mag_fft = (np.abs(fshift_))
plt.subplot(3, 2, 3)
plt.imshow(Z, cmap='gray')
plt.xlabel('wx=0, yx=10PI')
# plt.title('Z = sin(wx * X + wy * Y)')
plt.subplot(3, 2, 4)
plt.imshow(mag_fft, cmap='gray')
# plt.title('FT of Z')

wx = 10 * PI
wy = 10 * PI
Z = np.sin(wx * X + wy * Y)
fft_ = np.fft.fft2(Z)
fshift_ = np.fft.fftshift(fft_) 
mag_fft = (np.abs(fshift_))
plt.subplot(3, 2, 5)
plt.imshow(Z, cmap='gray')
plt.xlabel('wx=10PI, yx=10PI')
# plt.title('Z = sin(wx * X + wy * Y)')
plt.subplot(3, 2, 6)
plt.imshow(mag_fft, cmap='gray')
# plt.title('FT of Z')
plt.show()

# -*- coding: utf-8 -*-
"""
Created on Sun Apr  5 15:49:25 2020

@author: shini
"""

import os

import cv2
import numpy as np
import matplotlib.pyplot as plt

img_path_1 = '../test_img/4.jpg'
img_path_2 = '../test_img/22.jpg'

# img_list = os.listdir(img_path)

img_1 = cv2.imread(img_path_1, 0)
fft_1= np.fft.fft2(img_1)
fshift_1 = np.fft.fftshift(fft_1) 

## 提取傅里叶变换的实部，虚部
real_fft_1 = np.real(fshift_1)
imag_fft_1 = np.imag(fshift_1)

## 计算傅里叶变换的模
mag_fft_1 = np.abs(fshift_1)

## 对模取对数
log_mag_fft_1 = np.log(mag_fft_1)

## 逆傅里叶变换
ifft_img_1 = np.fft.ifft2(fshift_1)
i_img = np.abs(ifft_img_1)

img_2 = cv2.imread(img_path_2, 0)
fft_2 = np.fft.fft2(img_2)
fshift_2 = np.fft.fftshift(fft_2)

real_fft_2 = np.real(fshift_2)
imag_fft_2 = np.imag(fshift_2)

fshift_12 = real_fft_1 + imag_fft_2 * 1j
ifft_img_12 = np.fft.ifft2(fshift_12)
i_img_12 = np.abs(ifft_img_12)

fshift_21 = real_fft_2 + imag_fft_1 * 1j
ifft_img_21 = np.fft.ifft2(fshift_21)
i_img_21 = np.abs(ifft_img_21)

plt.figure()
plt.subplot(2, 2, 1)
plt.imshow(img_1, cmap='gray')
plt.subplot(2, 2, 2)
plt.imshow(img_2, cmap='gray')
plt.subplot(2, 2, 3)
plt.imshow(i_img_12, cmap='gray')
plt.subplot(2, 2, 4)
plt.imshow(i_img_21, cmap='gray')
plt.show()