K近邻算法实现手写数字识别系统
简单地说,K 近邻算法采用测量不同特征值之间的距离方法进行分类。
K 近邻算法的一般流程
1.收集数据:可以使用任何方法。
2.准备数据:距离计算所需要的数值,最好是结构化的数据格式。
3.分析数据:可以使用任何方法。
4.训练算法:此步骤不适用于 K 近邻算法。
5.测试算法:计算错误率。
6.使用算法:首先需要输入样本数据和结构化的输出结果,然后运行K 近邻算法判定输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。
准备:使用 Python 导入数据
首先,我们学习如何使用 Python 导入数据,这个过程非常简单。
import numpy as np
def createDataSet():
group = np.array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
labels = ['A', 'A', 'B', 'B']
return group, labels
在上面的代码中,我们导入科学计算包 NumPy,K 近邻算法执行排序操作时将使用这个模块提供的函数。
然后,我们尝试加载这些数据。
group, labels = createDataSet()
print('group:', group)
print('labels:', labels) # 输出数值
上述命令创建了变量 group 和 labels,在 Python 命令提示符下输入下列命令,输入变量的名字以检验是否正确地定义变量:
这里有 4 组数据,每组数据有两个我们已知的属性或者特征值。上面的 group 矩阵每行包含一个不同的数据,我们可以把它想象为某个日志文件中不同的测量点或者入口。由于人类大脑的限制,我们通常只能可视化处理三维以下的事务。因此为了简单地实现数据可视化,对于每个数据点我们通常只使用两个特征。
向量 labels 包含了每个数据点的标签信息,labels 包含的元素个数等于 group 矩阵行数。这里我们将数据点 (1, 1.1) 定义为类 A,数据点 (0, 0.1) 定义为类 B。为了说明方便,例子中的数值是任意选择的,并没有给出轴标签,图 2-2 是带有类标签信息的四个数据点。
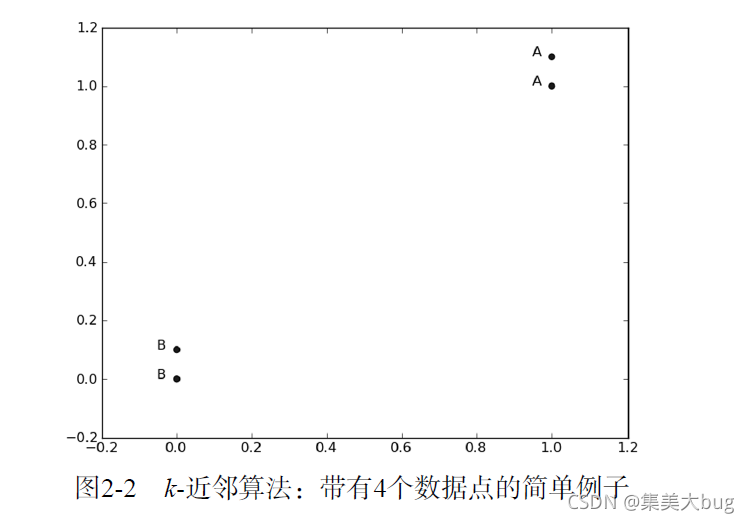
现在我们已经知道 Python 如何解析数据,如何加载数据,以及 K 近邻 算法的工作原理,接下来我们将使用这些方法完成分类任务。
使用 K 近邻分类器的手写识别系统。为了简单起见,这里构造的系统只能识别数字 0 到 9,参见图 2-6。需要识别的数字已经使用图形处理软件,处理成具有相同的色彩和大小 1:宽高是 32 像素 x 32 像素的黑白图像。
尽管采用文本格式存储图像不能有效地利用内存空间,但是为了方便理解,我们还是将图像转换为文本格式。

将图像转换为向量:该函数创建 1x1024 的 NumPy 数组,然后打开给定的文件,循环读出文件的前 32 行,并将每行的头 32 个字符值存储在 NumPy 数组中,最后返回数组。
def img2vector(filename):
# 创建向量
returnVect = np.zeros((1, 1024))
# 打开数据文件,读取每行内容
fr = open(filename)
for i in range(32):
# 读取每一行
lineStr = fr.readline()
# 将每行前 32 字符转成 int 存入向量
for j in range(32):
returnVect[0, 32*i+j] = int(lineStr[j])
return returnVect
然后,测试 img2vector 函数:
img2vector(‘digits/testDigits/0_1.txt’)
算法实现过程:
计算已知类别数据集中的点与当前点之间的距离;
按照距离递增次序排序;
选取与当前点距离最小的 k 个点;
确定前 k 个点所在类别的出现频率;
返回前 k 个点出现频率最高的类别作为当前点的预测分类。
import operator
def classify0(inX, dataSet, labels, k):
"""
参数:
- inX: 用于分类的输入向量
- dataSet: 输入的训练样本集
- labels: 样本数据的类标签向量
- k: 用于选择最近邻居的数目
"""
# 获取样本数据数量
dataSetSize = dataSet.shape[0]
# 矩阵运算,计算测试数据与每个样本数据对应数据项的差值
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
# sqDistances 上一步骤结果平方和
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1)
# 取平方根,得到距离向量
distances = sqDistances**0.5
# 按照距离从低到高排序
sortedDistIndicies = distances.argsort()
classCount = {}
# 依次取出最近的样本数据
for i in range(k):
# 记录该样本数据所属的类别
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
# 对类别出现的频次进行排序,从高到低
sortedClassCount = sorted(
classCount.items(), key=operator.itemgetter(1), reverse=True)
# 返回出现频次最高的类别
return sortedClassCount[0][0]
使用欧氏距离公式,计算两个向量点 之间的距离:

测试的步骤:
读取训练数据到向量(手写图片数据),从数据文件名中提取类别标签列表(每个向量对应的真实的数字)
读取测试数据到向量,从数据文件名中提取类别标签
执行K 近邻算法对测试数据进行测试,得到分类结果
与实际的类别标签进行对比,记录分类错误率
打印每个数据文件的分类数据及错误率作为最终的结果
from os import listdir
def handwritingClassTest():
# 样本数据的类标签列表
hwLabels = []
# 样本数据文件列表
trainingFileList = listdir('digits/trainingDigits')
m = len(trainingFileList)
# 初始化样本数据矩阵(M*1024)
trainingMat = np.zeros((m, 1024))
# 依次读取所有样本数据到数据矩阵
for i in range(m):
# 提取文件名中的数字
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = int(fileStr.split('_')[0])
hwLabels.append(classNumStr)
# 将样本数据存入矩阵
trainingMat[i, :] = img2vector(
'digits/trainingDigits/%s' % fileNameStr)
# 循环读取测试数据
testFileList = listdir('digits/testDigits')
# 初始化错误率
errorCount = 0.0
mTest = len(testFileList)
# 循环测试每个测试数据文件
for i in range(mTest):
# 提取文件名中的数字
fileNameStr = testFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = int(fileStr.split('_')[0])
# 提取数据向量
vectorUnderTest = img2vector('digits/testDigits/%s' % fileNameStr)
# 对数据文件进行分类
classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
# 打印 K 近邻算法分类结果和真实的分类
print("测试样本 %d, 分类器预测: %d, 真实类别: %d" %
(i+1, classifierResult, classNumStr))
# 判断K 近邻算法结果是否准确
if (classifierResult != classNumStr):
errorCount += 1.0
# 打印错误率
print("\n错误分类计数: %d" % errorCount)
print("\n错误分类比例: %f" % (errorCount/float(mTest)))