一、插值(interpolation)的定义
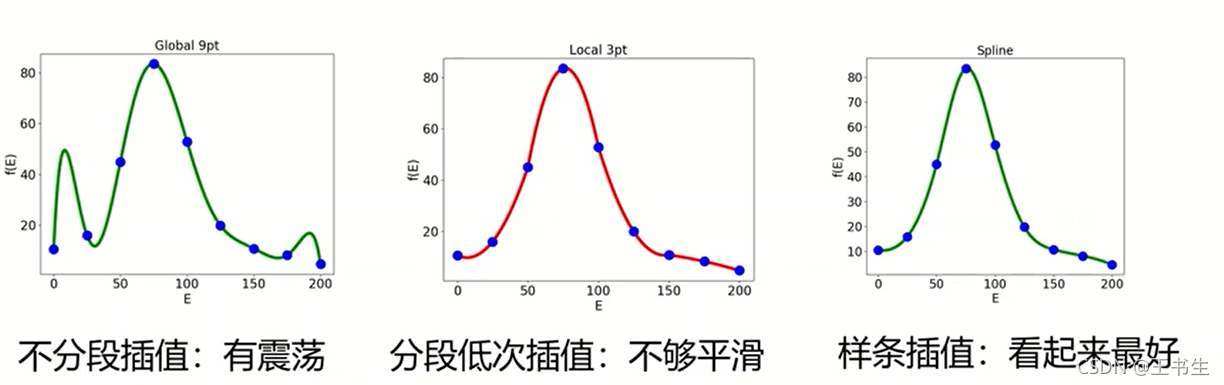
插值 :在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。
二、多项式插值
f
(
x
)
?
a
0
+
a
1
x
+
a
2
x
2
+
?
+
a
n
?
1
x
n
?
1
,
(
x
?
x
i
)
f(x) \simeq a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n-1} x^{n-1}, \quad\left(x \simeq x_{i}\right)
f(x)?a0?+a1?x+a2?x2+?+an?1?xn?1,(x?xi?).
三、拉格朗日插值法
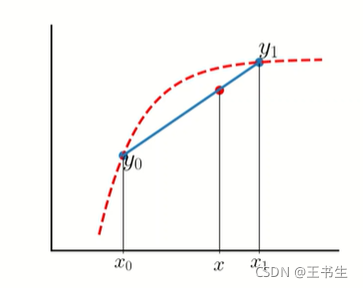
1. 线性插值
过两点
(
x
0
,
y
0
)
,
(
x
1
,
y
1
)
\left(x_{0}, y_{0}\right),\left(x_{1}, y_{1}\right)
(x0?,y0?),(x1?,y1?)的直线表达式构造为
y
=
x
?
x
1
x
0
?
x
1
y
0
+
x
?
x
0
x
1
?
x
0
y
1
y=\frac{x-x_{1}}{x_{0}-x_{1}} y_{0}+\frac{x-x_{0}}{x_{1}-x_{0}} y_{1}
y=x0??x1?x?x1??y0?+x1??x0?x?x0??y1?
将上式改写成
L
1
(
x
)
=
l
0
(
x
)
y
0
+
l
1
(
x
)
y
1
\quad L_{1}(x)=l_{0}(x) y_{0}+l_{1}(x) y_{1}
L1?(x)=l0?(x)y0?+l1?(x)y1?
l
0
(
x
)
,
l
1
(
x
)
满足:
l
0
(
x
0
)
=
1
,
l
0
(
x
1
)
=
0
l
1
(
x
0
)
=
0
,
l
1
(
x
1
)
=
1
\begin{array}{lll}l_{0}(x), l_{1}(x)\text{满足:}& l_{0}\left(x_{0}\right)=1, & l_{0}\left(x_{1}\right)=0 \\ & l_{1}\left(x_{0}\right)=0, & l_{1}\left(x_{1}\right)=1\end{array}
l0?(x),l1?(x)满足:?l0?(x0?)=1,l1?(x0?)=0,?l0?(x1?)=0l1?(x1?)=1?
是线性揷值函数的基函数,这种插值称为拉格朗日插值.
2. 二次拉格朗日插值基函数
利用3点构造二次拉格朗日揷值多项式:
L
2
(
x
)
=
l
0
(
x
)
y
0
+
l
1
(
x
)
y
1
+
l
2
(
x
)
y
2
L_{2}(x)=l_{0}(x) y_{0}+l_{1}(x) y_{1}+l_{2}(x) y_{2}
L2?(x)=l0?(x)y0?+l1?(x)y1?+l2?(x)y2? 是通过
(
x
0
,
y
0
)
,
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
\left(x_{0}, y_{0}\right),\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)
(x0?,y0?),(x1?,y1?),(x2?,y2?)三点的抛物线.则二次拉格朗日插值基函数:
{
l
0
(
x
)
=
(
x
?
x
1
)
(
x
?
x
2
)
(
x
0
?
x
1
)
(
x
0
?
x
2
)
l
1
(
x
)
=
(
x
?
x
0
)
(
x
?
x
2
)
(
x
1
?
x
0
)
(
x
1
?
x
2
)
l
2
(
x
)
=
(
x
?
x
0
)
(
x
?
x
1
)
(
x
2
?
x
0
)
(
x
2
?
x
1
)
\left\{\begin{array}{l} l_{0}(x)=\frac{\left(x-x_{1}\right)\left(x-x_{2}\right)}{\left(x_{0}-x_{1}\right)\left(x_{0}-x_{2}\right)} \\ \\ l_{1}(x)=\frac{\left(x-x_{0}\right)\left(x-x_{2}\right)}{\left(x_{1}-x_{0}\right)\left(x_{1}-x_{2}\right)} \\ \\ l_{2}(x)=\frac{\left(x-x_{0}\right)\left(x-x_{1}\right)}{\left(x_{2}-x_{0}\right)\left(x_{2}-x_{1}\right)} \end{array}\right.
??????????????l0?(x)=(x0??x1?)(x0??x2?)(x?x1?)(x?x2?)?l1?(x)=(x1??x0?)(x1??x2?)(x?x0?)(x?x2?)?l2?(x)=(x2??x0?)(x2??x1?)(x?x0?)(x?x1?)??
------------------------------------------------------------------------
l
0
(
x
0
)
=
1
l
0
(
x
1
)
=
0
l
0
(
x
2
)
=
0
l
1
(
x
0
)
=
0
l
1
(
x
1
)
=
1
l
1
(
x
2
)
=
0
l
2
(
x
0
)
=
0
l
2
(
x
1
)
=
0
l
2
(
x
2
)
=
1
\begin{array}{lll} l_{0}\left(x_{0}\right)=1 & l_{0}\left(x_{1}\right)=0 & l_{0}\left(x_{2}\right)=0 \\ l_{1}\left(x_{0}\right)=0 & l_{1}\left(x_{1}\right)=1 & l_{1}\left(x_{2}\right)=0 \\ l_{2}\left(x_{0}\right)=0 & l_{2}\left(x_{1}\right)=0 & l_{2}\left(x_{2}\right)=1 \end{array}
l0?(x0?)=1l1?(x0?)=0l2?(x0?)=0?l0?(x1?)=0l1?(x1?)=1l2?(x1?)=0?l0?(x2?)=0l1?(x2?)=0l2?(x2?)=1?
------------------------------------------------------------------------
用
y
=
f
(
x
)
y=f(x)
y=f(x)的
n
+
1
n+1
n+1个节点构造不超过
n
n
n次的拉格朗日插值多项式:
拉格朗日插值多项式:
L
n
(
x
)
=
∑
k
=
0
n
l
k
(
x
)
y
k
L_{n}(x)=\sum_{k=0}^{n} l_{k}(x) y_{k}
Ln?(x)=∑k=0n?lk?(x)yk?
拉格朗日插值基函数:
l
k
(
x
)
=
(
x
?
x
0
)
?
(
x
?
x
k
?
1
)
(
x
?
x
k
+
1
)
?
(
x
?
x
n
)
(
x
k
?
x
0
)
?
(
x
k
?
x
k
?
1
)
(
x
k
?
x
k
+
1
)
?
(
x
k
?
x
n
)
l_{k}(x)=\frac{\left(x-x_{0}\right) \cdots\left(x-x_{k-1}\right)\left(x-x_{k+1}\right) \cdots\left(x-x_{n}\right)}{\left(x_{k}-x_{0}\right) \cdots\left(x_{k}-x_{k-1}\right)\left(x_{k}-x_{k+1}\right) \cdots\left(x_{k}-x_{n}\right)}
lk?(x)=(xk??x0?)?(xk??xk?1?)(xk??xk+1?)?(xk??xn?)(x?x0?)?(x?xk?1?)(x?xk+1?)?(x?xn?)?
或写成: l k ( x ) = ∏ j = 0 , j ≠ k n ( x ? x j ) ( x k ? x j ) l_{k}(x)=\prod_{j=0, j \neq k}^{n} \frac{\left(x-x_{j}\right)}{\left(x_{k}-x_{j}\right)} lk?(x)=∏j=0,j?=kn?(xk??xj?)(x?xj?)?
3. Python代码实现Lagrange插值多项式
import numpy as np
import matplotlib.pyplot as plt
def Lagrange_interp(xdata,ydata,x):
'''
Lagrange插值代码,
参数设置:
xdata,ydata:已知数据
x:要插入数据的x坐标
'''
v = np.zeros(x.size) #插值结果数值
n = xdata.size
for k in range(n): #n个Lagrange多项式
w = np.ones(x.size) #记录连乘
for j in range(n):
if j != k:
w *= (x-xdata[j])/(xdata[k]-xdata[j])
v += w*ydata[k] # L_k(x)乘以对应函数值f(x_k)
return v
4. 实例:
import numpy as np
import matplotlib.pyplot as plt
'''
Lagrange插值代码,参数设置:xdata,ydata:已知数据x:要插入数据的x坐标
'''
def Lagrange_interp(xdata,ydata,x):
v = np.zeros(x.size) #插值结果数值
n = xdata.size
for k in range(n): #n个Lagrange多项式
w = np.ones(x.size) #记录连乘
for j in range(n):
if j != k:
w *= (x-xdata[j])/(xdata[k]-xdata[j])
v += w*ydata[k] # L_k(x)乘以对应函数值f(x_k)
return v
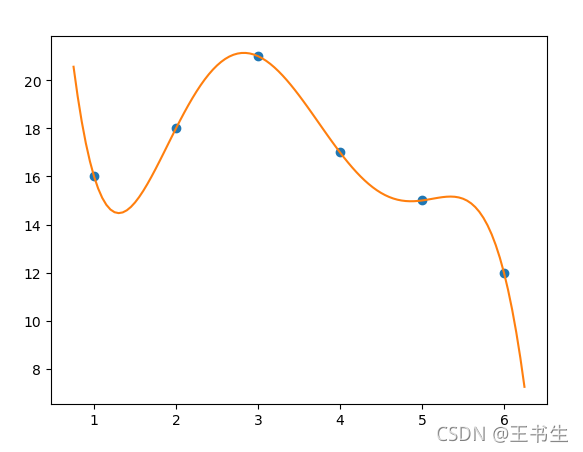
x = np.arange(1,7)
y = np.array([16,18,21,17,15,12])
u = np.arange(0.75,6.3,0.05)
v = Lagrange_interp(x,y,u)
plt.plot(x,y,'o',u,v,'-')
结果: