[人工智能] 【读书笔记】深度学习入门：基于python的理论与实现（1）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 【读书笔记】深度学习入门：基于python的理论与实现（1） -> 正文阅读

[人工智能]【读书笔记】深度学习入门：基于python的理论与实现（1）

第一二章比较基础和简单，不多赘述，主要包括python，python中矩阵运算常用库numpy的简单用法，和感知机的基本概念。python语言和numpy还是要提前学习比较好。

如果matplotlib库有报错：查看：
Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure 问题解决方法

第三章神经网络

??简单来说，神经网络有三层，输入层，中间层和输出层
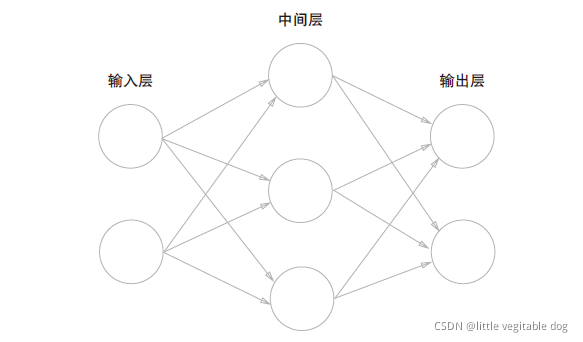
在这里插入图片描述
??但实际上只有两层神经元有权重，因此称为“2层网络”

神经网络中信号的传递方式：
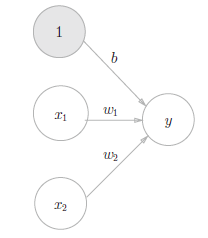
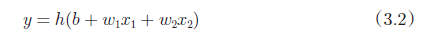
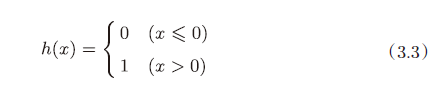
在这里插入图片描述

??输入信号的总和被函数h(x)转换，转换后的值就是输出y。然后式3.3 表示的函数h(x)，在输入超过0时返回1，否则返回0。
??刚才登场的h(x)函数会将输入信号的总和转换为输出信号，这种函数般称为激活函数( activation function)。如“激活”一词所示，激活函数的作用在于决定如何来激活输入信号的总和。
先计算输入信号的加权总和，然后用激活函数转换这一总和，因此，上述的式3.2 可以分为
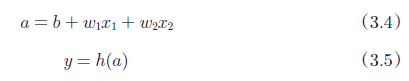
在这里插入图片描述
详细形式

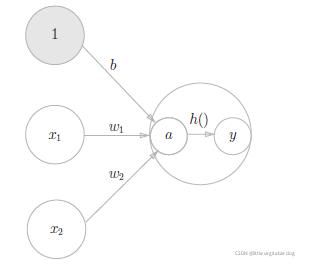
不同的激活函数：

sigmoid函数

??神经网络中用 sigmoid函数作为激活函数，进行信号的转换，转换后的信号被传送给下一个神经元。
实现：

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

阶跃函数

??输入大于0时输出为1，输入小于0时输出为0
sigmoid函数和阶跃函数比较：
??首先注意到的是**“平滑性”**的不同。 sigmoid函数是一条平滑的曲线，输出随着输入发生连续性的变化。而阶跃函数以0为界，输出发生急剧性的变化。 sigmoid函数的平滑性对神经网络的学习具有重要意义。
??sigmoid可以返回连续的实数值信号

共同点：都是非线性函数
?? 神经网络的激活函数必须使用非线性函数。（激活函数不能使用线性函数）
因为使用线性函数的话，加深神经网络的层数就没有意义了。线性函数的问题在于，不管如何加深层数，总是存在与之等效的“无隐藏层的神经网络”。为了具体地理解这一点，我们来思考下面这个简单的例子。这里我们考虑把线性函数h(x)=cx作为激活函数，把y(x)=h(h(h(x))）的运算对应3层神经网络。
??这个运算会进行y(x)=c×c×c×x的乘法运算，但是同样的处理可以由y(x)=ax(注意，a=c^3)这一次乘法运算（即没有隐藏层的神经网络）来表示。如本例所示，使用线性函数时，无法发挥多层网络带来的优势。因此，为了发挥叠加层所带来的优势，激活函数必须使用非线性函数。

ReLU函数（常用）

实现：

def relu(x):
    return np.maximum(0, x)

先介绍一些符号，w₁₂⁽¹⁾,a₁⁽¹⁾ 等
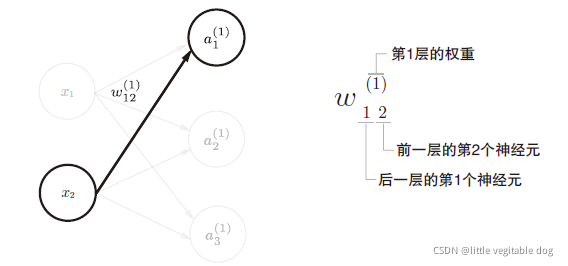
在这里插入图片描述
??权重和隐藏层的神经元右上角有一个（1）代表神经元的层号（即第一层的神经元）
??权重参数下角标的1,2的含义如图所示
各层间信号传递的实现：

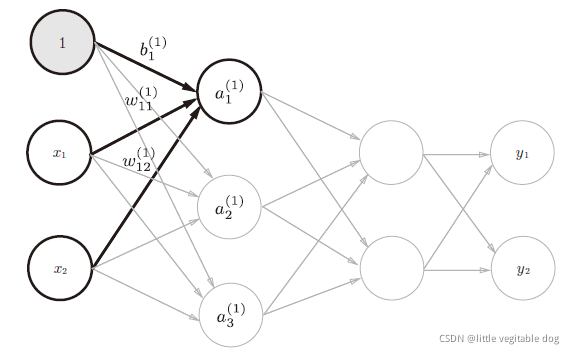
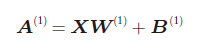
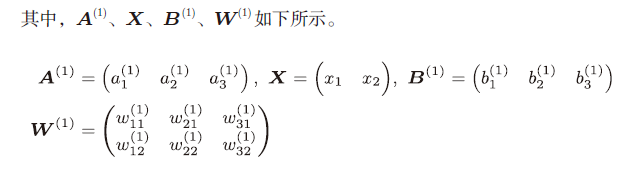
从输入层到第1层的信号传递：

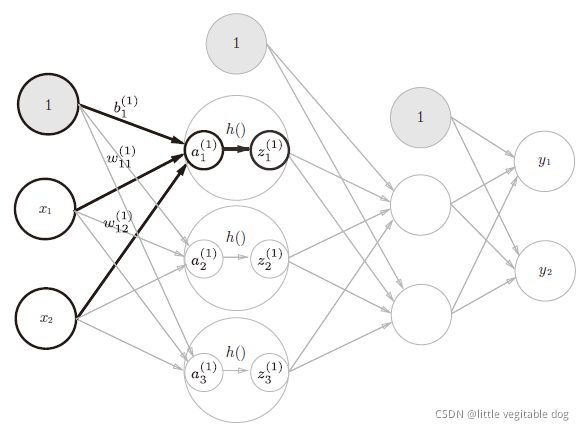
第一层到第2层的信号传递：

第2层到输出层的信号传递：

代码实现：

??权重记为W（数据格式设置为字典）定义网络的初始化和正向传播函数，前者进行权重和偏置的初始化，并保存在字典变量中，这个字典变量保存了每一层所需的参数（W和b），后者则封装了输入信号转换为输出信号的处理过程。

import numpy as np
import sigmoid as sigmoid


def identity_function(x):
    return x


def init_network():
    network = {'w1': np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]), 'b1': np.array([0.1, 0.2, 0.3]),
               'w2': np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]), 'b2': np.array([0.1, 0.2]),
               'w3': np.array([[0.1, 0.3], [0.2, 0.4]]), 'b3': np.array([0.1, 0.2])}
    return network


def forward(network, x):
    w1, w2, w3 = network['w1'], network['w2'], network['w3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, w1) + b1
    z1 = sigmoid.sigmoid(a1)
    a2 = np.dot(z1, w2) + b2
    z2 = sigmoid.sigmoid(a2)
    a3 = np.dot(z2, w3) + b3

    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)  #[0.31682708  0.69627909]