[人工智能]【opencv-python】轮廓操作

参考资料

• Contours in OpenCV

学习目标

• 理解轮廓是什么
• 学习如何找到并绘制轮廓
• 相关函数：cv.findContours(), cv.drawContours()

什么是轮廓

轮廓可以简单地解释为连接所有连续点（沿边界）的曲线，具有相同的颜色或灰度。轮廓是形状分析和对象检测和识别的有用工具。为了获得更好的准确性，使用二值图像。所以在找到轮廓之前，应该用阈值或Canny边缘检测算法先进行预处理。自OpenCV 3.2以后，findContours()不再对源图像进行修改。在应用中，查找轮廓就像从黑色背景中查找查找白色目标物体，所以在使用轮廓查找功能时，目标物体需要是白色的而背景需要是黑色的，这就是为什么要对二值图像进行预处理。下面我们看看如何在二值图像中查找轮廓。下面展示如何在二值图像中提取轮廓的代码：

import numpy as np
import cv2 as cv
im = cv.imread('test.jpg')
imgray = cv.cvtColor(im, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imgray, 127, 255, 0)
contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)

函数中由三个参数，第一是源图像，第二个是轮廓恢复模式，第三个是轮廓近似方法。函数输出轮廓和层级。输出轮廓的结果是包含图像中所有轮廓的一个Python列表。每个独立的轮廓是一个表现为（x,y）目标边界点坐标形式的Numpy数组。示例代码的功能基本上可以覆盖其他所有轮廓的提取任务。

如何绘制轮廓

画轮廓用cv.drawContours()函数。这个函数也可以用于任意形状且有边界点的轮廓。函数第一个参数是源图像，第二个参数是以Python列表形式传送的轮廓，第三个参数是轮廓的索引（如果画某个图像中单独的轮廓，这个选项就是有用的；如果先把图像中所有轮廓都画出来，这个参数就输入-1），其他剩余参数是轮廓颜色、厚度等等。

• 画图像中所有的轮廓：

cv.drawContours(img, contours, -1, (0,255,0), 3)

• 画第四个轮廓：

cv.drawContours(img, contours, 3, (0,255,0), 3)

• 大多数场景，下面的写法和上面的写法效果相同，但是放眼未来下面的这种写法却是更有用的 ：

cnt = contours[4]
cv.drawContours(img, [cnt], 0, (0,255,0), 3)

轮廓近似方法

轮廓近似方法选项就是cv.findContours()函数的第三个参数，那么这个参数实际意味着什么呢？前文所述，轮廓的本质就是具有相同灰度的轮廓形状，以形状边界的（x,y）点坐标形式存储。但是其是否存储所有的坐标，有这个轮廓近似方法确定。如果选“cv.CHAIN_APPROX_NONE”选项，所有的边界点都会储存，但是实际上不需要所有的边界点。例如，如果发现直线的轮廓，我们是否需要轮廓上全部的点去表示这条线？当然是不需要的，我只需要知道直线的两个端点就可以了，这些就可以用“cv.CHAIN_APPROX_SIMPLE”搞定，其可以移除冗余点并将轮廓压缩从而节省内存。下文的矩形图像阐释了这个技术，我们在轮廓阵列的所有坐标点上用蓝色绘制圆形，首先在第一张图像中展示用“cv.CHAIN_APPROX_NONE”（734个点）处理的轮廓，第二章图像显示用“cv.CHAIN_APPROX_SIMPlE”（只有四个点）提取的轮廓，由此可见这种操作节省了多少内存。

轮廓特征

主要涉及如何找到不同轮廓的特征，如面积、周长、边界框等等，与轮廓相关的功能还是非常多的。图像的moments能够辅助计算诸如目标质心、面积之类的特征，想要详细了解可以查阅维基百科相关页面。函数cv.moments()提供一个包含所有计算得到moment值得字典，参考如下代码：

import numpy as np
import cv2 as cv
img = cv.imread('star.jpg',0)
ret,thresh = cv.threshold(img,127,255,0)
contours,hierarchy = cv.findContours(thresh, 1, 2)
cnt = contours[0]
M = cv.moments(cnt)
print( M )

矩（MOMENTS）

从这个moments可以算出很多特征，如area、centroid。其中质心可以通过如下公式算出：
$$C_x=\frac{M_{10}}{M_{00}}，C_y=\frac{M_{01}}{M_{00}}$$
可以通过如下代码实现：

cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])

轮廓面积

轮廓面积由函数cv.contourArea()或矩M[‘m00’]给出，代码如下：

area = cv.contourArea(cnt)

轮廓周长

它也被称为弧长。可以使用cv.arcLength()函数实现功能。第二个参数指定形状是闭合轮廓（如果传递为True），还是仅为曲线。

perimeter = cv.arcLength(cnt,True)

轮廓近似

根据我们指定的精度，基于Douglas Peucker算法将一个轮廓形状近似为另一个顶点数较少的形状。为了理解这一点，假设试图在图像中找到一个正方形，但是由于图像中的一些问题没有得到一个完美的正方形，而是一个“坏形状”（如下面的第一幅图像所示），则可以使用此函数来近似形状。在这里，第二个参数称为ε，它是从轮廓到近似轮廓的最大距离，是一个表示精度参数。要获得正确的输出，需要正确地选择ε。

epsilon = 0.1*cv.arcLength(cnt,True)
approx = cv.approxPolyDP(cnt,epsilon,True)

在下图的第二幅图中，绿线显示了ε=0.1倍弧长的近似曲线。第三幅图显示了epsilon=弧长的1%的情况。第三个参数指定曲线是否闭合。

凸包

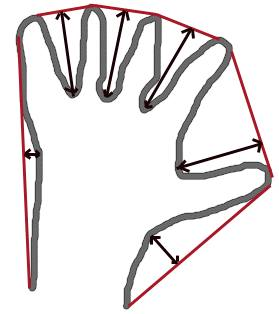
凸包看起来类似于轮廓近似，但事实并非如此（在某些情况下，两者可能提供相同的结果）。在这里，cv.convexHull()函数检查曲线的凸度缺陷并对其进行纠正。一般来说，凸曲线是指总是凸出的曲线，或者至少是平坦的曲线。如果内部凸起，则称为凸面缺陷。例如，检查下面的手的图像。红线显示手的凸面外壳。双面箭头标记显示凸面缺陷，即包与轮廓的局部最大偏差。
关于它的语法可以讨论一些内容：

hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]]])

函数参数细节说明如下：

• points：传入的轮廓；
• hull：是输出，一般我们不写；
• clockwise：方向标志位，如果为真，则输出凸包的方向为顺时针。否则其方向为逆时针方向；
• returnPoints：返回点，默认情况下为True返回外壳点的坐标，如果为False，则返回与外壳点对应的轮廓点索引。

因此为了得到形如上述图像的凸包，下列事项是非常重要的：

hull = cv.convexHull(cnt)

但如果要查找凸性缺陷，则需要传递returnPoints=False。为了理解它，我们将使用上面的矩形图像。首先我发现它的轮廓是cnt。现在我发现它的凸包返回点=True，我得到以下值：[[234 202]]，[[51 202]]，[[51 79]]，[[234 79]]]，它们是矩形的四个角点。现在，如果对returnPoints=False执行相同的操作，我将得到以下结果：[[129]、[67]、[0]、[142]]。这些是轮廓线中对应点的索引值。例如，检查第一个值：cnt[129]=[[234, 202]]，该值与第一个结果相同（其他值也是如此）。简单的说，如果returnPoints为True，就直接返回点，否则就返回点的索引值。当后面讨论凸性缺陷时，将再次看到这些内容。

凸性检测

cv.isContourConvex()函数可以检查曲线是否凸，它只返回正确或错误。

k = cv.isContourConvex(cnt)

边框

有两种类型的边界矩形。

• 直边矩形：就是一个直矩形且不考虑物体的旋转。所以此时边框的面积不会是最小的。它由函数cv.boundingRect()找到。下面代码中，(x,y)代表图像左上方向为原点的坐标系，(w,h)是边框的长和高，如下代码所示：

x,y,w,h = cv.boundingRect(cnt)
cv.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2)

• 旋转矩形：此时边界矩形是以最小面积绘制的，因此它考虑了旋转。使用的函数是cv.minareact()，返回一个包含以下详细信息的Box2D结构-（中心（x，y）、（宽度、高度）、旋转角度）。但是要画这个矩形，我们需要矩形的四个角，由函数cv.boxPoints()获得。

rect = cv.minAreaRect(cnt)
box = cv.boxPoints(rect)
box = np.int0(box)
cv.drawContours(img,[box],0,(0,0,255),2)

直边矩形（绿色）和旋转矩形（红色）都在下面的图中展示出来了。

最小外接圆

我们使用函数cv.MineConclosingCircle()查找对象的外接圆，即一个以最小面积完全覆盖物体的圆。代码如下：

center = (int(x),int(y))
radius = int(radius)
cv.circle(img,center,radius,(0,255,0),2)

拟合椭圆

将对象轮廓拟合为一个椭圆，并返回椭圆能内接的旋转矩形，代码如下：

ellipse = cv.fitEllipse(cnt)
cv.ellipse(img,ellipse,(0,255,0),2)

效果如下图所示：

拟合直线

近似地，可以针对一组点拟合一条直线，下图包含了一组白色的点，可以将它们近似逼近为一条直线，代码如下：

rows,cols = img.shape[:2]
[vx,vy,x,y] = cv.fitLine(cnt, cv.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
cv.line(img,(cols-1,righty),(0,lefty),(0,255,0),2)

运行效果如下图所示：

轮廓性质

此处我们获取目标轮廓的一些常用属性，如坚固度、等效直径、遮罩图像、平均灰度等。更多功能可在Matlab regionprops文档中找到。质心、面积、周长等也属于轮廓性质这一类，但是这些内容已经在前文提及了。

纵横比（Aspect Ratio ）

目标边界矩形的宽度与高度之比。
$$AspectRatio=\frac{Width}{Height}$$

x,y,w,h = cv.boundingRect(cnt)
aspect_ratio = float(w)/h

限度（Extent）

限度（Extent）就是轮廓面积和边框矩形的比值，用公式表示如下：

$$Extent=\frac{ObjectArea}{BoundingRectangleArea}$$

示例代码如下：

area = cv.contourArea(cnt)
x,y,w,h = cv.boundingRect(cnt)
rect_area = w*h
extent = float(area)/rect_area

坚固度（Solidity）

坚固度是轮廓面积和凸包面积之比
$$Solidity=\frac{ContourArea}{ConvexHullArea}$$

area = cv.contourArea(cnt)
hull = cv.convexHull(cnt)
hull_area = cv.contourArea(hull)
solidity = float(area)/hull_area

等效直径（Equivalent Diameter）

等效直径就是通过轮廓面积计算出来的圆直径。
$$EquivalentDiameter=\sqrt{\frac{4\times ContourArea}{\pi }}$$
示例代码：

area = cv.contourArea(cnt)
equi_diameter = np.sqrt(4*area/np.pi)

方向（Orientation）

方向就是目标指向的角度，下面显示的函数也能给出长轴和短轴长度。

(x,y),(MA,ma),angle = cv.fitEllipse(cnt)

掩膜和像素点（Mask and Pixel Points）

在某些情况下，我们需要包含目标的所有像素点，可以通过下列代码实现：

mask = np.zeros(imgray.shape,np.uint8)
cv.drawContours(mask,[cnt],0,255,-1)
pixelpoints = np.transpose(np.nonzero(mask))
#pixelpoints = cv.findNonZero(mask)

这里给出了两种方法，一种使用Numpy函数，另一种使用OpenCV函数（最后一行注释）来实现同样的功能。结果也一样，但略有不同。Numpy以**（行、列）格式给出坐标，而OpenCV以（x、y）**格式给出坐标。所以基本上答案会互换。请注意，行=y，列=x。

最大/最小值和相应位置（Maximum Value, Minimum Value and their locations ）

我们可以使用掩膜图像计算出这些参数：

min_val, max_val, min_loc, max_loc = cv.minMaxLoc(imgray,mask = mask)

平均颜色和平均灰度

可以找到目标的平均颜色，或者得到在灰度模式下的平均灰度，这些还可以通过相同的掩膜方法实现：

mean_val = cv.mean(im,mask = mask)

极值点

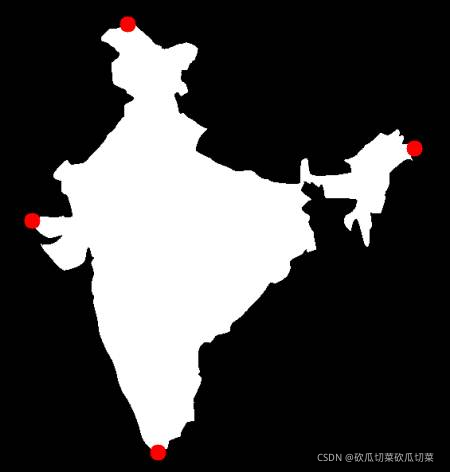
极值点是指目标的最上面、最下面、最右边和最左边的点。

leftmost = tuple(cnt[cnt[:,:,0].argmin()][0])
rightmost = tuple(cnt[cnt[:,:,0].argmax()][0])
topmost = tuple(cnt[cnt[:,:,1].argmin()][0])
bottommost = tuple(cnt[cnt[:,:,1].argmax()][0])

这是个印度的地图，得到下列结果：

其它更多函数

学习目标

• 凸性缺陷及其查找方法；
• 找到从一个点到多边形的最短距离；
• 匹配不同形状

理论和相关代码

凸性缺陷

之前已经熟悉了什么事凸包，目标与凸包之间的偏差可以视为凸性缺陷。OpenCV中的函数cv.convexityDefects()可以实现这个功能，示例代码如下：

hull = cv.convexHull(cnt,returnPoints = False)
defects = cv.convexityDefects(cnt,hull)

寻找凸包的时候，要设置returnPoints = False以便找到凸性缺陷。返回值是一个数组，形如[ start point, end point, farthest point, approximate distance to farthest point ]. 同时可以使用图像对其进行可视化，通过一条连接首末点，然后在最远点画个圆，前三个返回值是轮廓的索引，因此需要从cnt中读取到这些值，示例代码如下所示：

import cv2 as cv
import numpy as np
img = cv.imread('star.jpg')
img_gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
ret,thresh = cv.threshold(img_gray, 127, 255,0)
contours,hierarchy = cv.findContours(thresh,2,1)
cnt = contours[0]
hull = cv.convexHull(cnt,returnPoints = False)
defects = cv.convexityDefects(cnt,hull)
for i in range(defects.shape[0]):
    s,e,f,d = defects[i,0]
    start = tuple(cnt[s][0])
    end = tuple(cnt[e][0])
    far = tuple(cnt[f][0])
    cv.line(img,start,end,[0,255,0],2)
    cv.circle(img,far,5,[0,0,255],-1)
cv.imshow('img',img)
cv.waitKey(0)
cv.destroyAllWindows()

运行结果如下图所示：

感谢支持，欢迎关注，丰富技术/学术内容持续更新！

opencv-python快速入门视频教程