[人工智能]多示例多标签论文Multi-instance multi-label learning浅读分析

Multi-instance multi-label learning

周志华教授在这篇文章内讲了很多东西，这个博客只是简单的将其提出算法的大概意思叙述一遍，也为自己以后的阅读留点印象。这里附上ScienceDirect的论文链接：点这里.

摘要

在本文中，我们提出了 MIML（多示例多标签学习）框架，其中一个样本由多个实例描述并与多个类标签相关联。与传统的学习框架相比，MIML 框架对于表示具有多种语义含义的复杂对象更加方便和自然。为了从 MIML 样本中学习，我们提出了基于简单退化策略的 MimlBoost 和 MimlSvm 算法，实验表明，在 MIML 框架中解决涉及具有多种语义含义的复杂对象的问题可以带来良好的性能。考虑到退化过程可能会丢失信息，我们提出了直接在正则化框架中解决 MIML 问题的 D-MimlSvm 算法。此外，我们表明，即使我们无法访问真实对象，因此无法通过使用 MIML 表示从真实对象中获取更多信息，MIML 仍然有用。我们提出了 InsDif 和 SubCod 算法。 InsDif 的工作原理是将单实例转换为 MIML 表示进行学习，而 SubCod 的工作原理是将单标签示例转换为 MIML 表示进行学习。实验表明，在某些任务中，它们能够获得比直接学习单实例或单标签示例更好的性能。

基本思想

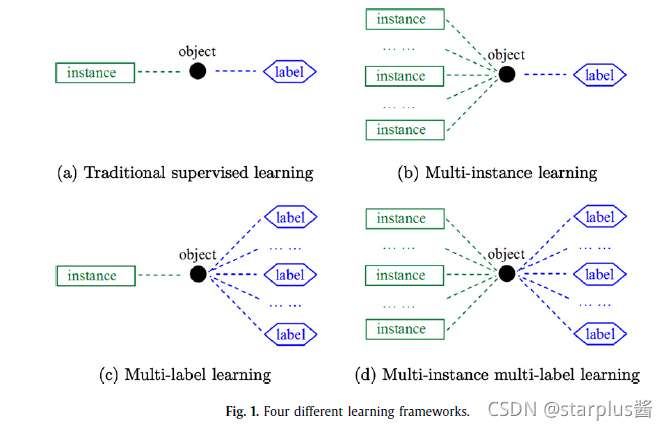
可以看出，上图中的四种学习框架归根结底就是数据结构的不同。各个框架的特点都是见名知义的。可以简单归纳为：

1. 单实例单标签(SISL)：一个对象由一个实例描述，且对应一个标签。
2. 多示例单标签(MISL)：一个对象由多个实例描述，且对应一个标签。
3. 单实例多标签(SIML)：一个对象由一个实例描述，且对应多个标签。
4. 多示例多标签(MIML)：一个对象由多个实例描述，且对应多个标签。
   可以看出，MIML能够更好地描述对象，其标签信息也更充分。

退化算法

在此主要介绍几种基于退化的算法，即将MIML问题退化成多示例学习或者多标签学习。

MIMLBoost

此算法将MIML问题转化为多示例问题进行处理。假设标签数为$U$，则对于一个MIML对象$(X,Y)$可以分解为$U$个MI对象，即：$[(X,Y_1),(X,Y_2),?,(X,Y_u)],u\in [1,?,U]$。举例说明，假设一个MIML对象为$(X,[1,0,1,0])$，其中$[1,0,1,0]$为标签。则这个对象转化为MI对象后的表示为$[(X,1),(X,0),(X,1),(X,0)]$。在将所有训练MIML对象转化为MI的包表示之后，再使用$U$个已有的多示例算法MIBoosting对其学习。总的来说，MIMLBoost算法将一个含有$N$个MIML对象和$U$个标签的数据集按照标签列分为了$U$个数据集，每个数据集用一个MIBoosting算法单独学习。在测试阶段，$U$个算法的结果拼接起来就得到新包的预测多标签。

MIMLSVM

此算法将MIML问题转化为多标签问题进行处理，即将包转化为单实例。假设MIML数据集用$(\mathcal{X},\mathcal{Y})$表示，我们首先在$\mathcal{X}$上使用k-medoids聚类算法，得到$k$个簇。假设$k$为3且用$X$表示包，且簇中心为$X_1,X_2,X_3$，则对于包$X_i$，其转化为的单向量为$[dis(X_i,X_1),dis(X_i,X_2),dis(X_i,X_3)]$。当所有包都转化为单向量后，MIML问题就转化为了传统的ML问题，在使用传统ML算法MLSVM进行训练和预测。

MIMLSVM${}_{mi}$

此算法与MIMLBoost算法相同，只是将MIMLBoost内部的多示例算法MIBoosting替换为另一个多示例算法MI-SVM。

MIMLNN

此算法为MIMLSVM的变体，即将MIMLSVM内部的MLSVM替换为两层的神经网络。

主要算法

上一章介绍的四种基于退化的算法会在一定程度上损失信息，例如包内实例的相关性或者标签之间的相关性。所以本文还提出了一种通过正则化来“直接”处理MIML结构的数据，目前还没有看明白，后面再补。

转换算法

在文章发表的时期，MIML的数据集还不是很多见。所以作者还提出了两种转换方法INSDIF和SUBCOD，用以通过MIML框架处理单实例多标签问题和多示例单标签问题。INSDIF算法将单实例多标签(SIML)问题转化为MIML问题，即将单实例转化为包。SUBCOD算法将多示例单标签(MISL)问题转化为MIML问题，即将单标签数据转化为多标签。这两种算法的提出并非为了强行解释，其中INSDIF算法可以将混合在单实例中的信息分隔开，有利于学习。
而SUBCOD算法可以分理出主要标签的子标签，也是更利于学习。

ISNDIF

文中的ISNDIF(Instance Differentiation)算法包含两个阶段，第一阶段将单实例转化为多示例，第二阶段采用某种MIML算法进行学习，在此就只介绍第一阶段的做法，即将单实例多标签数据转化为MIML数据。
首先，ISNDIF需要得到一组原型实例，其个数为标签个数。每个原型实例为训练集中所有属于其对应标签的实例的均值向量。
对于每个实例，它与每个原型实例相减都会得到一个向量，则这些相减得到的向量就作为原始单向量转换成的包。
则对于转换后的数据集，每个包的大小相同且都为标签个数。
以下为一个小例子：

上图中，因为标签数为3，所以能获得三个原型实例，且包大小为3。
对于第一个标签，其所属的实例有①②④，则第一个标签对应的原型实例为(①+②+④) / 3。
同理可得第二个标签的原型实例为(②+③+④) / 3。
第三个为(①+③+④+⑤) / 4。
由此得到如下三个原型实例：

则实例①转化为的包应该为 { [ ① ? a ] , [ ① ? b ] , [ ① ? c ] } \{[①-a], [①-b], [①-c]\} {[①?a],[①?b],[①?c]}，同理可得其他实例的转化结果。

SUBCOD

SUBCOD算法关注如何将原始单标签的子标签(sub-concepts)挖掘出来，从而实现单标签到多标签的转化。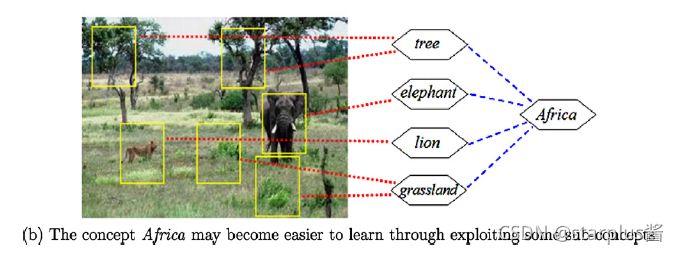
如上图所示，“Africa”的原始标签下其实能够分出很多子标签，例如：tree， elephant， lion， grassland。通过这种标签级别的分解，单标签到多标签的转化就能够实现了。
跟INSDIF一样，SUBCOD原本包含了单标签转化为多标签和在多标签上学习这两个阶段，但是这里只描述第一阶段。
需要注意的是，SUBCOD算法是用来将多示例单标签数据转化为MIML数据的。步骤如下：

1. 首先将所有包打开，得到实例空间 D = { x 1 , x 2 , ? ? , x N } D=\{\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_N\} D={x1?,x2?,?,xN?}。
2. 一个拥有$M$个分布的高斯混合分布(GMM)将基于EM算法来拟合所有实例(这一步可直接使用sklearn中的GMM类实现)。$M$即表示多标签的类别数。
3. 在GMM训练完成之后，我们可以得到每个实例对于这$M$个分布的隶属度向量，然后找到此向量中最大值的索引作为该实例所属的分布。
4. 然后再第三步的基础上考虑样本的原始标签。(此步还没看明白)