参考资料
[1] 强化学习入门 第四讲 时间差分法(TD方法)
本文主要是对该资料学习的笔记,并且加入了一些自己的想法,如有错误欢迎指出。
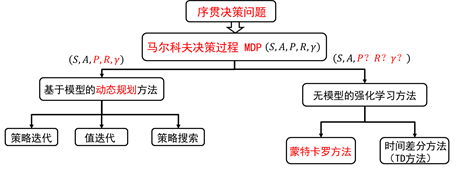
强化学习的分类
无模型强化学习 - 理论
强化学习的核心问题
强化学习的核心问题为:
- 策略评估部分:值函数、状态-行为值函数的估计问题!
- 策略改善部分:给定值函数下, π ( a ∣ s ) \pi(a|s) π(a∣s)的选取问题!
回报函数、值函数定义
累计回报函数
G
t
=
R
t
+
1
+
γ
R
t
+
2
+
.
.
.
=
∑
k
=
0
∞
γ
k
R
t
+
k
+
1
(1.1)
G_t = R_{t+1} + \gamma R_{t+2} + ... = \sum^{\infty}_{k=0} \gamma ^{k}R_{t+k+1} \tag{1.1}
Gt?=Rt+1?+γRt+2?+...=k=0∑∞?γkRt+k+1?(1.1)
状态值函数
v
π
(
s
)
=
E
π
[
G
t
]
=
E
π
[
∑
k
=
0
∞
γ
k
R
t
+
k
+
1
∣
S
t
=
s
]
(1.2)
v_\pi (s) = E_\pi[G_t] = E_\pi \left[ \sum^{\infty}_{k=0} \gamma ^{k}R_{t+k+1} | S_t = s \right] \tag{1.2}
vπ?(s)=Eπ?[Gt?]=Eπ?[k=0∑∞?γkRt+k+1?∣St?=s](1.2)
行为值函数
q
π
(
s
,
a
)
=
E
π
[
∑
k
=
0
∞
γ
k
R
t
+
k
+
1
∣
S
t
=
s
,
A
t
=
a
]
(1.3)
q_\pi (s,a) = E_\pi \left[ \sum^{\infty}_{k=0} \gamma ^{k}R_{t+k+1} | S_t = s , A_t = a \right] \tag{1.3}
qπ?(s,a)=Eπ?[k=0∑∞?γkRt+k+1?∣St?=s,At?=a](1.3)
可见状态值函数和行为值函数的定义是在策略
π
\pi
π下各次实现中累计回报函数的数学期望。
动态规划方法值函数:
V
(
s
t
)
=
∑
a
∈
A
π
(
a
∣
s
)
(
R
s
a
+
γ
∑
s
′
P
s
s
′
a
V
(
s
′
)
)
(1.4)
V (s_t) = \sum_{a \in A} \pi(a|s)\left( R^a_s + \gamma\sum_{s'} P^{a}_{ss'}V(s') \right) \tag{1.4}
V(st?)=a∈A∑?π(a∣s)(Rsa?+γs′∑?Pss′a?V(s′))(1.4)
动态规划方法值函数的计算用到了后继状态的值函数,利用bootstrapping方法,即用后继状态的值函数估计当前值函数。此时期望值由模型提供。
蒙特卡罗方法值函数:
V
(
s
t
)
=
V
(
s
t
)
+
α
(
G
t
?
V
(
s
t
)
)
=
(
1
?
α
)
V
(
s
t
)
+
α
G
t
(1.5)
V (s_t) = V (s_t) + \alpha(G_t-V(s_t)) = (1-\alpha)V (s_t) + \alpha G_t \tag{1.5}
V(st?)=V(st?)+α(Gt??V(st?))=(1?α)V(st?)+αGt?(1.5)
蒙特卡罗方法利用经验平均估计状态的值函数,即利用多次历史实验中该状态的平均累计回报函数来逼近期望。
时间差分法的引出
蒙特卡罗方法的缺点:需要等好一次试验完成后才可利用经验平均估计值函数。
为解决该问题:
- 参考动态规划法的booststrapping自举方法,利用后继状态估计当前值函数;
- 参考蒙特卡罗方法,使用试验估计值函数。
时间差分法的值函数
先给出TD法值函数的公式:
V
(
S
t
)
←
V
(
S
t
)
+
α
(
R
t
+
1
+
γ
V
(
S
t
+
1
)
?
V
(
S
t
)
)
(2.1)
V(S_t) \leftarrow V(S_t) + \alpha(R_{t+1} + \gamma V(S_{t+1}) - V(S_t)) \tag{2.1}
V(St?)←V(St?)+α(Rt+1?+γV(St+1?)?V(St?))(2.1)
V ( S t ) ← ( 1 ? α ) V ( S t ) + α ( R t + 1 + γ V ( S t + 1 ) ) (2.2) V(S_t) \leftarrow (1-\alpha)V(S_t) + \alpha(R_{t+1} + \gamma V(S_{t+1})) \tag{2.2} V(St?)←(1?α)V(St?)+α(Rt+1?+γV(St+1?))(2.2)
其中:
- R t + 1 + γ V ( S t + 1 ) R_{t+1} + \gamma V(S_{t+1}) Rt+1?+γV(St+1?)定义为TD目标
- δ t = R t + 1 + γ V ( S t + 1 ) ? V ( S t ) \delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t) δt?=Rt+1?+γV(St+1?)?V(St?)定义为TD偏差
(2.2)式为个人便于理解的形式。
与蒙特卡罗法在方差上的对比,参考[1]:
蒙特卡罗法利用对各次实验获得的累计回报函数(1.1)式求平均来逼近值函数,为无偏估计。每次得到的 G t G_t Gt?值要等到最终状态出现,要经历很多随机的状态和动作,因此每次得到的 G t G_t Gt?随机性很大,因此方差无穷大。
时间差分方法中若 V ( S t + 1 ) V(S_{t+1}) V(St+1?)采用真实值,则是无偏估计,但实际中 V ( S t + 1 ) V(S_{t+1}) V(St+1?)是估计值,因此时间差分估计方法属于有偏估计。然而,跟蒙特卡罗方法相比,时间差分方法只用到了一步随机状态和动作,因此TD目标的随机性比蒙特卡罗方法中的 G t G_t Gt?要小,因此其方差也比蒙特卡罗方法的方差小。
基于时间差分法的强化学习算法
有了(2.1)式,现在可以给出on-policy的Sarsa强化学习算法和off-policy的Qlearning强化学习算法:
- Sarsa
- Q-Learning
可以看出,异策略的Qlearning方法与同策略的Sarsa方法主要差别在于Q的更新。在QLearning中由于更新的算法为贪婪算法所以需要取代表贪婪策略的maxQ(s,a)。
从算法中可以明确看到为什么说TD为有偏估计:公式中 V ( S t + 1 ) V(S_{t+1}) V(St+1?)在理论上是与未来状态有关的量,但实际中采用了仍在逐步更新的、可能尚未收敛的值来计算。
T D ( λ ) TD(\lambda) TD(λ)方法
G
t
(
1
)
=
R
t
+
1
+
γ
V
(
S
t
+
1
)
G_{t}^{(1)} = R_{t+1} + \gamma V(S_{t+1})
Gt(1)?=Rt+1?+γV(St+1?)表示使用t时刻的下一步t+1时刻的值函数
V
(
S
t
+
1
)
V(S_{t+1})
V(St+1?)和当前的回报来估计该次实验的累计回报函数。
G
t
(
2
)
=
R
t
+
1
+
γ
R
t
+
2
+
γ
2
V
(
S
t
+
2
)
G_{t}^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^{2} V(S_{t+2})
Gt(2)?=Rt+1?+γRt+2?+γ2V(St+2?)表示使用t时刻后t+2时刻的值函数
V
(
S
t
+
2
)
V(S_{t+2})
V(St+2?)和当前及下一步的回报来估计该次实验的累计回报函数。
…
G
t
(
n
)
=
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
.
.
.
+
γ
n
?
1
R
t
+
n
+
γ
n
V
(
S
t
+
2
)
G_{t}^{(n)} = R_{t+1} + \gamma R_{t+2} + \gamma^{2}R_{t+3} + ... + \gamma^{n-1}R_{t+n} + \gamma^{n} V(S_{t+2})
Gt(n)?=Rt+1?+γRt+2?+γ2Rt+3?+...+γn?1Rt+n?+γnV(St+2?)表示使用t时刻后t+n时刻的值函数
V
(
S
t
+
2
)
V(S_{t+2})
V(St+2?)和当前及往后n步的回报来估计该次实验的累计回报函数。
将上式加权融合:
G
t
λ
=
(
1
?
λ
)
G
t
(
1
)
+
(
1
?
λ
)
λ
G
t
(
2
)
+
.
.
.
+
(
1
?
λ
)
λ
n
?
1
G
t
(
n
)
≈
V
(
S
t
)
(3)
G_t^{\lambda} = (1-\lambda)G_t^{(1)} + (1-\lambda)\lambda G_t^{(2)} + ... + (1-\lambda)\lambda^{n-1} G_t^{(n)} \approx V(S_t) \tag{3}
Gtλ?=(1?λ)Gt(1)?+(1?λ)λGt(2)?+...+(1?λ)λn?1Gt(n)?≈V(St?)(3)
T D ( λ ) TD(\lambda) TD(λ)方法即为用(3)式来更新当前状态值函数的方法。即加权融合后面n个状态的值函数来更新当前的值函数。
当 λ = 0 \lambda = 0 λ=0时,等价于之前说的TD方法。
[1]中对 T D ( λ ) TD(\lambda) TD(λ)方法的两种理解:
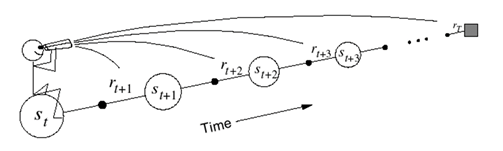
- T D ( λ ) TD(\lambda) TD(λ)前向视角
假设一个人坐在状态流上拿着望远镜看向前方,前方是那些将来的状态。当估计当前状态的值函数时, T D ( λ ) TD(\lambda) TD(λ)的定义中可以看到,它需要用来将来时刻的值函数。也就是说, T D ( λ ) TD(\lambda) TD(λ)前向观点通过观看将来状态的值函数来估计当前的值函数。
前向视角下的 T D ( λ ) TD(\lambda) TD(λ)方法值函数公式如下:
V
(
S
t
)
←
V
(
S
t
)
+
α
(
G
t
(
λ
)
?
V
(
S
t
)
)
(3.1)
V(S_t) \leftarrow V(S_t) + \alpha(G^{(\lambda)}_t - V(S_t)) \tag{3.1}
V(St?)←V(St?)+α(Gt(λ)??V(St?))(3.1)
G
t
λ
=
(
1
?
λ
)
∑
n
=
1
∞
(
1
?
λ
)
λ
n
?
1
G
t
(
n
)
(3.2)
G_t^{\lambda} = (1-\lambda)\sum_{n=1}^{\infty}(1-\lambda)\lambda^{n-1} G_t^{(n)} \tag{3.2}
Gtλ?=(1?λ)n=1∑∞?(1?λ)λn?1Gt(n)?(3.2)
G
t
(
n
)
=
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
.
.
.
(3.3)
G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \gamma^{2}R_{t+3} + ... \tag{3.3}
Gt(n)?=Rt+1?+γRt+2?+γ2Rt+3?+...(3.3)
从公式中可以看出前向视角下的 T D ( λ ) TD(\lambda) TD(λ)方法计算用到了将来时刻的值函数,因此需要等到整个试验结束后才对值函数进行集中更新。
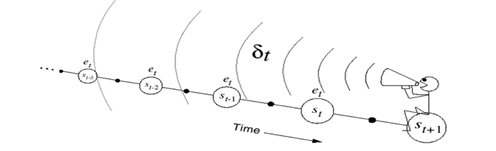
- T D ( λ ) TD(\lambda) TD(λ)后向视角
人骑坐在状态流上,手里拿着话筒,面朝已经经历过的状态流,获得当前回报并利用下一个状态的值函数得到TD偏差后,此人会向已经经历过的状态喊话,告诉这些已经经历过的状态处的值函数需要利用当前时刻的TD偏差进行更新。此时过往的每个状态值函数更新的大小应该跟距离当前状态的步数有关。假设当前状态为 S t S_t St?,TD偏差为 δ t \delta_t δt? ,那么 s t ? 1 s_{t-1} st?1?处的值函数更新应该乘以一个衰减因子 γ λ \gamma \lambda γλ,状态 s t ? 2 s_{t-2} st?2?处的值函数更新应该乘以 ( γ λ ) 2 (\gamma \lambda)^2 (γλ)2 ,以此类推。
后向视角下的
T
D
(
λ
)
TD(\lambda)
TD(λ)方法值函数算法如下:

从算法中可以看出后向视角下的 T D ( λ ) TD(\lambda) TD(λ)方法计算在一次状态变化后就可进行更新,但需要更新空间中的所有状态。
利用 T D ( λ ) TD(\lambda) TD(λ)的 S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)算法如下:
T D ( λ ) TD(\lambda) TD(λ)方法与原始的 T D TD TD方法相比复杂度提升很多,其目的在于取得更好的估计效果。