机器学习 —— 感知机简单入门
第1关:感知机 - 西瓜好坏自动识别
1. 感知机原理简介
1.1 举例
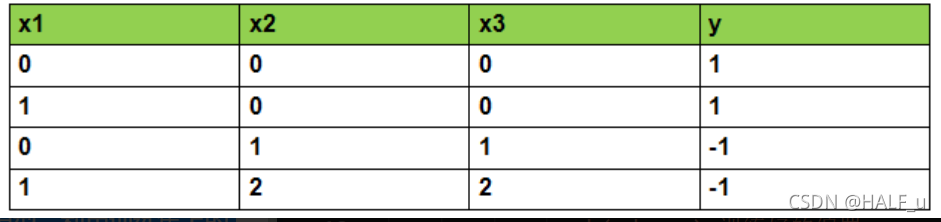
这里,我们利用西瓜书上的例子来构造数据,实例中包括特征和类别。一共构造了帮助预测的特征一共有 30 个:色泽、根蒂、敲声等等。类别为是好瓜与不是好瓜。部分数据如下:

由于我们的模型只能对数字进行计算。所以,我们用x1表示色泽,x2表示根蒂,x3表示敲声 。y 表示类别。其中,x1 = 0,表示青绿,x2 = 2,表示稍蜷, y=-1,表示不是好瓜。具体如下图:
而我们的任务就是,用感知机算法建立一个模型,利用训练集上的数据对模型进行训练,并对测试集上的数据进行分类。
1.2 数学原理/公式
我们知道神经网络是由一个个的神经元所组成的,我们知道了神经元的工作原理,就能帮助我们理解神经网络是如何工作的了。上个世纪六十年代,提出了最早的“人造神经元”模型,叫做“感知机”,直到今天还在用。感知机与逻辑回归一样,也是一个二分类模型,那么它又是如何进行预测的呢?
假如,我们希望构建一个感知机模型,根据色泽、根蒂、敲声这三个特征来判断是好瓜还是坏瓜。
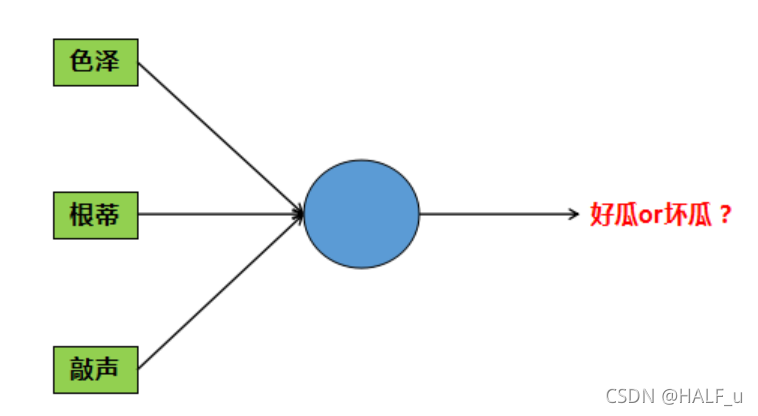
比如说,输入的特征值分别是青绿,蜷缩,浊响对应特征向量为 (0,0,0)。感知机模型会将每一个特征值xi乘以一个对应的权重wi ,再加上一个偏置 b,所得到的值如果大于等于 0,则判断为 +1 类别,即为好瓜,如果得到的值小于 0,则判断为 -1 类别,即不是好瓜。数学模型如下:

我们能否正确对西瓜好坏进行预测,完全取决于权重与偏置的值是否正确,那么如何找到正确的参数呢?方法与逻辑回归相似,这里就不重复叙述,唯一不同的就是感知机模型所用的损失函数。

那么,感知机使用的损失函数是怎么样的呢?
感知机采用的损失函数最初采用的是误分类点到决策边界的距离为:

又因为:
- 1/||w|| 不影响 -y(w.x+b) 正负的判断,我们只需要判断 -y(wx+b) 的正负来判断分类的正确与否。所以 1/||w|| 对感知机学习算法的中间过程可有可无。
- 1/||w|| 不影响感知机学习算法的最终结果。因为感知机学习算法最终的终止条件是所有的输入都被正确分类,即不存在误分类的点。则此时损失函数为 0。对应于 -y(wx+b)/||w|| ,即分子为 0。则可以看出 1/||w|| 对最终结果也无影响。所以最后采用的损失函数为:

1.3 算法流程
感知机只针对误分类的点对参数进行更新,算法流程如下:
- 选取初始值 w0 ,b0 ;
- 在训练集中选取数据xi ,yi ;
- 如果yi (w.xi +b)≤0,即这个点为误分类点,则进行如下更新(η为学习率,为0到1之间的值):
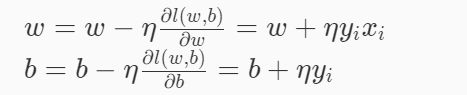
- 重复 2,3 直到训练集中没有误分类点
2. 实现代码
#encoding=utf8
import numpy as np
#构建感知机算法
class Perceptron(object):
def __init__(self, learning_rate = 0.01, max_iter = 200):
self.lr = learning_rate
self.max_iter = max_iter
def fit(self, data, label):
'''
input:data(ndarray):训练数据特征
label(ndarray):训练数据标签
output:w(ndarray):训练好的权重
b(ndarry):训练好的偏置
'''
# 编写感知机训练方法,w为权重,b为偏置
self.w = np.array([1.]*data.shape[1])
self.b = np.array([1.])
# 选择初值w0,b0
# 当shape[0]时,得到的是矩阵的行数
# 当shape[1]时,得到的是矩阵的列数
# [1.] == [1.0] 数据集的每一项变成浮点数吗?然后在转换为ndarry?
#********* Begin *********#
i = 0
while i < self.max_iter:
flag = True
for j in range(len(label)):
if label[j] * (np.inner(self.w, data[j]) + self.b) <= 0:
flag = False
self.w += self.lr * (label[j] * data[j])
self.b += self.lr * label[j]
if flag:
break
i+=1
#********* End *********#
def predict(self, data):
'''
input:data(ndarray):测试数据特征
output:predict(ndarray):预测标签
'''
#********* Begin *********#
y = np.inner(data, self.w) + self.b
# np.inner(a,b) 两个数组的内积
for i in range(len(y)): # range(0,6)
# print(list(range(0,6))) --> [0, 1, 2, 3, 4, 5]
if y[i] >= 0:
y[i] = 1
else:
y[i] = -1
predict = y
#********* End *********#
return predict
第2关:scikit-learn感知机实践 - 癌细胞精准识别
1. 数据集介绍及使用
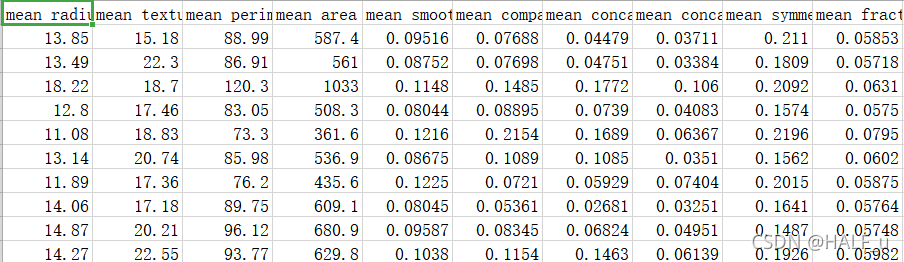
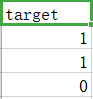
乳腺癌数据集,其实例数量是 569,实例中包括诊断类和属性,帮助预测的属性一共 30 个,各属性包括为 radius 半径(从中心到边缘上点的距离的平均值), texture 纹理(灰度值的标准偏差)等等,类包括:WDBC-Malignant 恶性和 WDBC-Benign 良性。用数据集的 80% 作为训练集,数据集的 20% 作为测试集,训练集和测试集中都包括特征和诊断类。
想要使用该数据集可以使用如下代码:
import pandas as pd
#获取训练数据
train_data = pd.read_csv('./step2/train_data.csv')
#获取训练标签
train_label = pd.read_csv('./step2/train_label.csv')
train_label = train_label['target']
#获取测试数据
test_data = pd.read_csv('./step2/test_data.csv')
数据集中部分数据与标签如下图所示:
2. 使用 sklearn.Perceptron 方法实现感知机算法
在 sklearn 中,使用 Perceptron 方法实现感知机算法,Perceptron 的构造函数中有两个常用的参数可以设置:
- eta0:学习率大小,默认为 1.0 ;
- max_iter:最大训练轮数。
和 sklearn 中其他分类器一样, Perceptron 类中的 fit 函数用于训练模型, fit 函数有两个向量输入:
- X :大小为 [样本数量,特征数量] 的 ndarray,存放训练样本;
- Y :值为整型,大小为 [样本数量] 的 ndarray,存放训练样本的分类标签。
Perceptron 类中的 predict 函数用于预测,返回预测标签, predict 函数有一个向量输入:
- X :大小为[样本数量,特征数量]的 ndarray ,存放预测样本。
Perceptron 的使用代码如下:
from sklearn.linear_model.perceptron import Perceptron
clf = Perceptron()
clf.fit(X_train, Y_train)
result = clf.predict(X_test)
3.题目编程要求
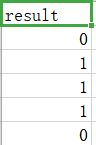
在 begin-end 之间补充代码,使用 sklearn 构建感知机模型,利用训练集数据与训练标签对模型进行训练,然后使用训练好的模型对测试集数据进行预测,并将预测结果保存到./step2/result.csv中。保存格式如下:
测试说明:我们会获取你的预测结果与真实标签对比,预测正确率高于 90% 视为过关。
4. 实现代码
#encoding=utf8
import os
if os.path.exists('./step2/result.csv'):
os.remove('./step2/result.csv')
#********* Begin *********#
import pandas as pd
#获取训练数据
train_data = pd.read_csv('./step2/train_data.csv')
#获取训练标签
train_label = pd.read_csv('./step2/train_label.csv')
train_label = train_label['target']# 取标签为target的一列
#获取测试数据
test_data = pd.read_csv('./step2/test_data.csv')
from sklearn.linear_model.perceptron import Perceptron
clf = Perceptron(eta0 = 0.01,max_iter = 200)
# 如果采用默认参数,预测正确率仅50%,不能达到过关标准
# 0.01,200的参数设置是参照感知机第一关设计
# max_iter = 1000,eta0 = 0.1, random_state = 666 为另一种参数设置参考
# 上述两种都可过关
clf.fit(train_data, train_label)
result = clf.predict(test_data)
frameResult = pd.DataFrame({'result':result})
frameResult.to_csv('./step2/result.csv', index = False)
#********* End *********#
# pandas的I/O API是一组read函数,
# 比如pandas.read_csv() (opens new window)函数。
# 这类函数可以返回pandas对象。
# 相应的write函数是像DataFrame.to_csv() (opens new window)一样的对象方法。
5. sklearn.Perceptron方法详述
英语好的直接看这个:官方手册
英语不好的看这个:面向csdn学习
本次实验中会涉及的相关知识点:
5.1 参数提及
| 参数名称 | 参数取值 | 参数解释 | 通俗解释 |
|---|---|---|---|
| max_iter | int整数,默认=1000 | 最大迭代次数,哪怕损失函数依旧大于0 | 梯度下降(寻找最优解的方法之一)时迭代的次数 |
| eta0 | 取值双精度浮点型double,默认=1 | 学习率,决定梯度下降时每次参数变化的幅度 | theta改变式子中的alpha学习捋?我猜的 |
| shuffle | bool值,默认=True | 每轮训练后是否打乱数据 | 结合下面这个参数一起看 |
| random_state | 取值为int, RandomState instance or None,默认=None | 当 shuffle =True时,用于打乱训练数据 | 结合上面这个参数一起看 |
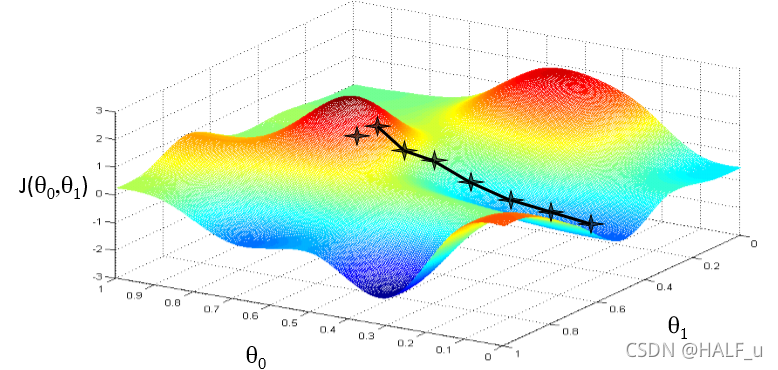
5.2 梯度下降法简单介绍


学习率:
-
如果α大小,结果是它一点一点的挪动,非常的缓慢,需要很多步才能到达全局最低点。
-
如果α太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛乃至发散。知道你发现实际上离最低点越来越远。
-
如果θ1初始化在局部最低点,在这儿,它已经在一个局部的最优处或局部最低点。结果是此处的导数是0,那么θ1将不会变,一直是原来的那个θ1,这也解释了为什么即使学习速率α不变时,梯度下降法也可以收敛局部最低点。
学习率换一种说法解释:
- 梯度下降算法每次迭代受到α的影响
- 如果α过小,则达到收敛所需的跌打次数将很大;
- 如果α过大,每次迭代可能不会减小代价函数的值,反而会远离局部最小值导致无法收敛。
- 通常可以考虑的下面这些学习率
- α = 0.01,0.03,0.1,0.3,1,3,10

迭代次数与学习率密切相关。
个人感觉,shuffle打乱数据是为了减少数据顺序导致的运算结果偶然性,类似如下二图:
一种下山情况:
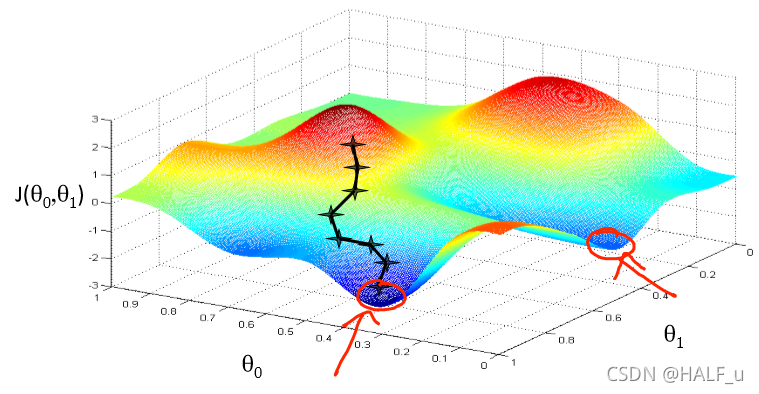
另一种下山情况: