为什么需要对数值类型的特征做归一化?
对数值类型的特征做归一化可以将所有的特征都统一到一个大致相同的数值区间内。最常用的方法主要有以下两种。
- 线性函数归一化(Min-Max Scaling)。它对原始数据进行线性变换,使得结果映射到[0,1]的范围,实现对原始数据的等比缩放。归一化公式如下
X n o r m = X ? X m i n X m a x ? X m i n X_{norm}=\frac{X-X_{min}}{X_{max}-X_{min}} Xnorm?=Xmax??Xmin?X?Xmin??
其中 X X X为原始数据, X m i n 、 X m a x X_{min}、X_{max} Xmin?、Xmax?分别为数据最大值和最小值。 - 零均值归一化(Z-Score Normalization)。它会将原始数据映射到均值为0、标准差为1的分布上。具体来说,假设原始特征的均值为
μ
\mu
μ、标准差为
σ
\sigma
σ,那么归一化为
z = x ? μ σ z=\frac{x-\mu}{\sigma} z=σx?μ?
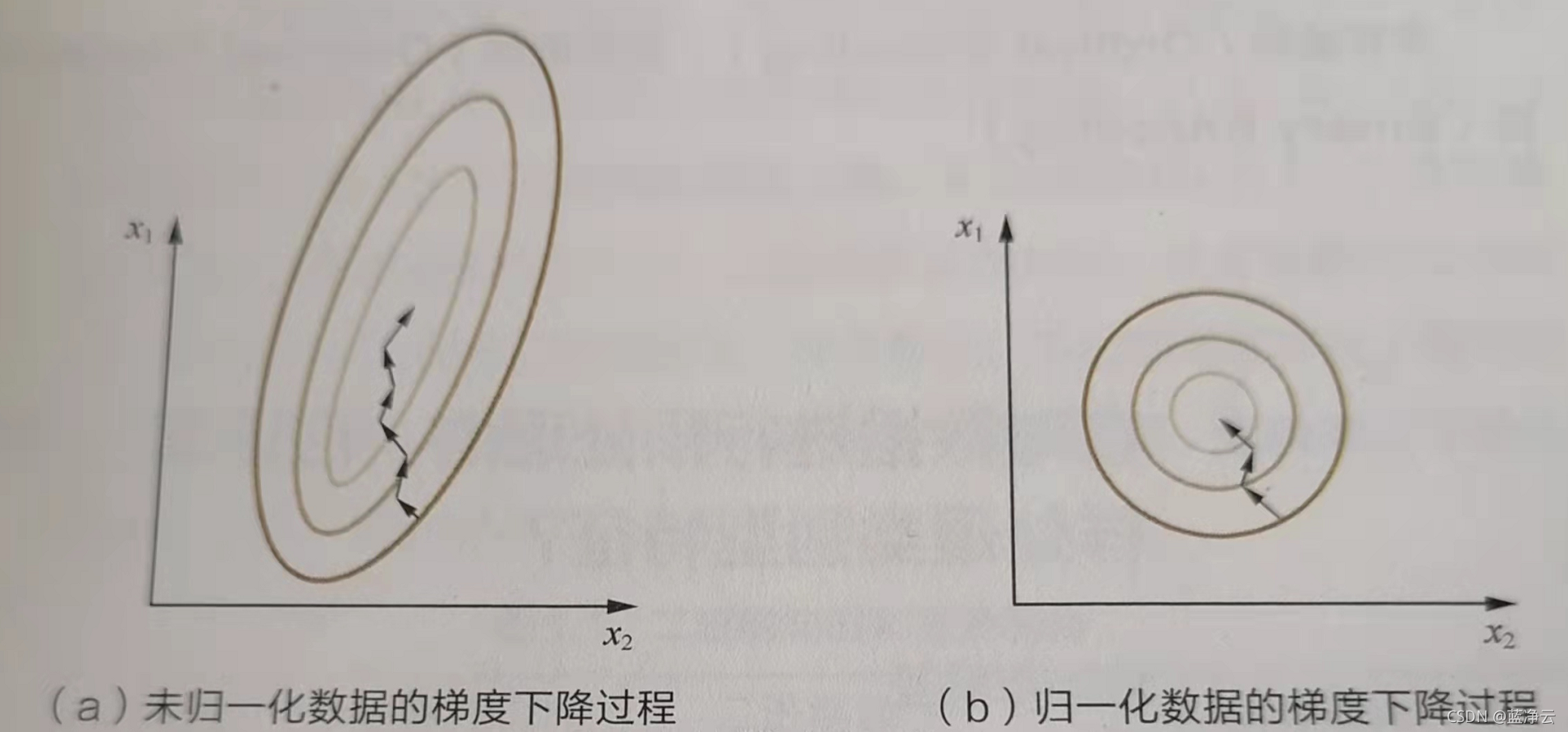
为什么需要对数值型特征做归一化呢?我们不妨借助随机梯度下降的实例来说明归一化的重要性。假设有两种数值型特征, x 1 x_1 x1?的取值范围是[0,10], x 2 x_2 x2?的取值范围是[0,3],于是可以构造一个目标函数图(a)中的等值图。
在学习率相同的情况下, x 1 x_1 x1?的更新速度会大于 x 2 x_2 x2?,需要更多的迭代才能找到最优解。如果将 x 1 x_1 x1?和 x 2 x_2 x2?归一化到相同的数值区间后,优化目标的等值图会变成图(b)中的圆形, x 1 x_1 x1?和 x 2 x_2 x2?的更新速度变得更为一致,容易更快地通过梯度下降找到最优解。
当然,数据归一化并不是万能的。在实际应用中,通过梯度下降法求解的模型通常是需要归一化的,包括线性回归、逻辑回归、支持向量机、神经网络等模型。但对决策树模型则并不适用,决策树在进行节点分裂时主要依据数据集D关于特征x的信息增益比,而信息增益比跟特征是否经过归一化是无关的,因为归一化并不会改变样本在特征x上的信息增益。