心得体会
本次主要学习了时间序列分析中的几种移动平均和指数平滑的时间序列处理方法,并实践了配套的R语言代码,体会到不同算法直接的联系与区别,部分算法是前身算法的加强与改进。
在这里感谢datawhale开源社区的小伙伴们给予的学习帮助,今后的学习也要一样加油呀
提示:以下是本篇文章正文内容
时间序列综述
时间序列也称动态序列,是指将某种现象的指标数值按照时间顺序排列而成的数值序列。其应用方向可大致分成三个部分,分别是描述过去、分析规律
和预测未来。
影响时间序列的因素
- 长期变动趋势(T)、
- 季节变动规律(S)、
- 周期变动规律(C)
- 不规则变动(I)(也称随机扰动项)
叠加模型和乘积模型
如果四种变动之间是相互独立的关系,那么叠加模型可以表示为:
Y = T + S + C + I
如果四种变动之间存在相互影响关系,那么应该使用乘积模型:
Y = T × S × C × I
一、简单移动平均法
移动平均法是根据时间序列资料逐渐推移,依次计算包含一定项数的时序平均数,以反映长期趋势的方法。当时间序列的数值由于受周期变动和不规则变动的影响,起伏较大,不易显示出发展趋势时,可用移动平均法,消除这些因素的影响,分析、预测序列的长期趋势。
如果数据具有一定的规律性,且一直在某一个值附近波动,那么我们可以用该组数据的平均值来近似拟合下一次可能出现的值。

当历史序列的基本趋势变化不大且序列中随机变动成分较多时,N 的取值应较大一些。否则N 的取值应小一些。在有确定的季节变动周期的资料中,移动平均的项数应取周期长度。选择最佳N 值的一个有效方法是,比较若干模型的预测误差。预测标准误差最小者为好。简单移动平均法只适合做近期预测,而且是预测目标的发展趋势变化不大的情况。如果目标的发展趋势存在其它的变化,采用简单移动平均法就会产生较大的预测偏差和滞后。
二、加权移动平均法
在简单移动平均公式中,每期数据在求平均时的作用是等同的。但是,每期数据所包含的信息量不一样,近期数据包含着更多关于未来情况的信息。因此,把各期数据等同看待是不尽合理的,应考虑各期数据的重要性,对近期数据给予较大的权重,这就是加权移动平均法的基本思想。

在加权移动平均法中,wt 的选择,同样具有一定的经验性。一般的原则是: 近期数据的权数大,远期数据的权数小。至于大到什么程度和小到什么程度,则需要按照预测者对序列的了解和分析来确定。
三、趋势移动平均法
简单移动平均法和加权移动平均法,在时间序列没有明显的趋势变动时,能够准确反映实际情况。但当时间序列出现直线增加或减少的变动趋势时,用简单移动平均法和加权移动平均法来预测就会出现滞后偏差。因此,需要进行修正,修正的方法是作二次移动平均,利用移动平均滞后偏差的规律来建立直线趋势的预测模型。这就是趋势移动平均法。

四、指数平滑法
一次移动平均实际上认为最近N 期数据对未来值影响相同,都加权1/N ; 而N 期以前的数据对未来值没有影响,加权为0。但是,二次及更高次移动平均数的权数却不是1/N ,且次数越高,权数的结构越复杂,但永远保持对称的权数,即两端项权数小,中间项权数大,不符合一般系统的动态性。一般说来历史数据对未来值的影响是随时间间隔的增长而递减的。所以,更切合实际的方法应是对各期观测值依时间顺序进行加权平均作为预测值。指数平滑法可满足这一要求,而且具有简单的递推形式。指数平滑法根据平滑次数的不同,又分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。
1、一次指数平滑法

α的选择:
- 如果时间序列波动不大,比较平稳,则α 应取小一点,如(0.1~0.5)。以减少
修正幅度,使预测模型能包含较长时间序列的信息; - 如果时间序列具有迅速且明显的变动倾向,则α 应取大一点,如(0.6~0.8)。
使预测模型灵敏度高一些,以便迅速跟上数据的变化。
2、二次指数平滑法
一次指数平滑法虽然克服了移动平均法的缺点。但当时间序列的变动出现直线趋势时,用一次指数平滑法进行预测,仍存在明显的滞后偏差。因此,也必须加以修正。修正的方法与趋势移动平均法相同,即再作二次指数平滑,利用滞后偏差的规律建立直线趋势模型。这就是二次指数平滑法。
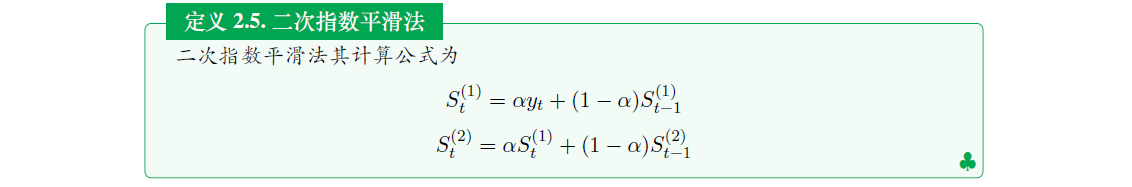
3、三次指数平滑法
当时间序列的变动表现为二次曲线趋势时,则需要用三次指数平滑法。三次指数平滑是在二次指数平滑的基础上,再进行一次平滑,计算式定义如下:

选择α值的准则:
- 如果序列的基本趋势比较稳,预测偏差由随机因素造成,则α 值应取小一些,以减
少修正幅度,使预测模型能包含更多历史数据的信息。 - 如果预测目标的基本趋势已发生系统的变化,则α 值应取得大一些。这样,可以偏
重新数据的信息对原模型进行大幅度修正,以使预测模型适应预测目标的新变化。
参考资料:
开源仓库:https://github.com/datawhalechina/team-learning-data-mining/tree/master/TimeSeries