[人工智能]Task 01：决策树（上）打卡（学习内容简单总结+课后题自解

Task1：学习链接：

Part A: 决策树 — Datawhale (datawhalechina.github.io)

学习到的知识：

1. 从信息论中引入信息熵，此作为判断节点不纯度，通过分裂来降低子节点的平均不纯度。
2. 熟悉了信息熵的理论定义、性质（关于n增大，极值等）；信息增益的定义。这层了解比之前仅仅了解三个公式（信息增益、信息增益比、GINI指数好多了）。
3. 从sklearn对ID3, C4.5，CART的实现中了解他们之间的区别。例如对连续变量的处理、缺失值的处理，以及找分割点的方式（最佳分割、随机分割），树生长的两种模式（深度优先和最佳增益）。
4. 了解CART与ID3, C4.5的区别，原来信息增益（不纯度的减少）还可以用MSE, MAE来度量；gini指数的引入是因为log不好计算，搞得对数函数再p=1处的一阶泰勒近似得到的gini指数
5. 关于决策树的剪枝，有预剪枝和后剪枝，之前只直到李航课本上的后剪枝，了解的更加全面，重要的是，自己能够从原理上推这样剪枝是合理的；关于剪枝的实现，了解了一些参数的意义，他们都有什么作用，以后调参总算是不会乱调了。
6. 整个教程很好，从为什么，理论证明，怎么做，理论证明，实现上大体是怎样的，参数的介绍等非常清楚。

练习部分自己的解答

【练习1】定义$X,Y$的联合熵为$H(Y,X)$?为$E(Y,X)～p(y,x)[?{\log }_{2}p(Y,X)]$?

• 请证明如下关系： $G(Y,X)=H(X)?H(X|Y)$??,$G(Y,X)=H(X)+H(Y)?H(Y,X)$?,$G(Y,X)=H(Y,X)?H(X|Y)?H(Y|X)$????
• 下图被分为了A、B和C三个区域。若AB区域代表X的不确定性，BC区域代表Y的不确定性，那么$H(X)$???、$H(Y)$???、$H(X|Y)H(X|Y)$???、$H(Y|X)$???、$H(Y,X)$???和$G(Y,X)$???,$G(Y,X)$???分别指代的是哪片区域？

1、首先证明 $G(Y,X)=H(X)?H(X|Y)$

右式子：
$$\begin{array}{rl}H(X)?H(X|Y)& ={\mathbb{E}}_X[?{\log }_{2}p(x)]?{\mathbb{E}}_Y{\mathbb{E}}_{X|Y}[?{\log }_{2}P(X|Y)]\\ & =?\sum _{m=1}^{M}p(x_m){\log }_{2}p(x_m)+\sum _{k=1}^K\sum _{m=1}^{M}p(x_m|y_k){\log }_{2}p(x_m|y_k)\\ & =?\sum _{k=1}^K[\sum _{m=1}^{M}p(x_m,y_k){\log }_{2}p(x_m)]+\sum _{k=1}^K\sum _{m=1}^{M}p(y_k)\frac{p(x_m,y_k)}{p(y_k)}{\log }_2\frac{p(x_m,y_k)}{p(y_k)}\\ & =\sum _{k=1}^K\sum _{m=1}^{M}p(x_m,y_k)[{\log }_2\frac{p(x_m,y_k)}{p(x_m)p(y_k)}]\\ & =?\sum _{k=1}^K\sum _{m=1}^{M}p(x_m,y_k)[{\log }_2\frac{p(x_m)p(y_k)}{p(x_m,y_k)}]\end{array}$$
上面等式结果等于$G(Y,X)=H(Y)?H(Y|X)=?{\sum }_{k=1}^K{\sum }_{m=1}^{M}p(x_m,y_k)[{\log }_2\frac{p(x_m)p(y_k)}{p(x_m,y_k)}]$?

故证得$G(Y,X)=H(X)?H(X|Y)$.

2、再证明$G(Y,X)=H(X)+H(Y)?H(Y,X)$

右边 =
$$\begin{array}{rl}& H(X)+H(Y)?H(Y,X)\\ & ={\mathbb{E}}_X[?{\log }_{2}p(X)]+{\mathbb{E}}_Y[?{\log }_{2}p(Y)]?{\mathbb{E}}_Y{\mathbb{E}}_{Y,X}[?{\log }_{2}P(Y,X)]\\ & =?\sum _{m=1}^{M}p(x_m){\log }_{2}p(x_m)?\sum _{k=1}^{K}p(y_k){\log }_{2}p(y_k)+\sum _{k=1}^K\sum _{m=1}^{M}p(y_k,x_m){\log }_{2}p(y_k,x_m)\\ & =?\sum _{m=1}^M[\sum _{k=1}^{K}p(y_k,x_m){\log }_{2}p(x_m)]?\sum _{k=1}^K[\sum _{m=1}^{M}p(y_k,x_m){\log }_{2}p(y_k)]+\sum _{k=1}^K\sum _{m=1}^{M}p(y_k,x_m){\log }_{2}p(y_k,x_m)\\ & =?\sum _{k=1}^K\sum _{m=1}^{M}p(y_k,x_m){\log }_2\frac{p(y_k,x_m)}{p(y_k)p(x_m)}\end{array}$$
同1，这与$G(Y,X)$相等

3、证明$G(Y,X)=H(Y,X)?H(X|Y)?H(Y|X)$

由于
$$\begin{array}{rl}G(Y,X)& =H(Y)?H(Y|X)(1)\\ G(Y,X)& =H(X)?H(X|Y)(2)\\ G(Y,X)& =H(X)+H(Y)?H(Y,X)(3)\end{array}$$
(1) + (2) - (3) 即可得$G(Y,X)=H(Y,X)?H(X|Y)?H(Y|X)$?

问题二：
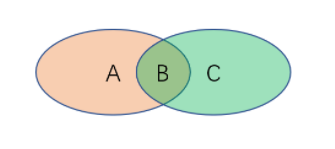$$\begin{array}{r}B:H(X,Y)\\ A:H(Y|X)\\ C:H(X|Y)\\ A\cup B:H(X)\\ B\cup C:H(Y)\\ B:G(Y,X)\end{array}$$

【练习2】假设当前我们需要处理一个分类问题，请问对输入特征进行归一化回对树模型的类别输出产生影响嘛？请解释原因。

不会产生影响。因为无论我们使用的是ID3，C4.5或者说是CART, 其树的生成都是基于概率来进行计算的，而归一化的作用仅仅是对数值特征进行放缩，它会影响到我分裂节点的取值，但是并不会影响到分裂节点的大小分布，所以说，对于一个分类问题而言，特征的归一化不会对分类的结果产生影响。

【练习3】如果将系数替换为$1?{\gamma }^2$，请问对缺失值是增强了还是削弱了惩罚。

$\gamma$取值范围为$[0,1]$，在这个区间内，${\gamma }^2$?的取值是小于$\gamma$的，所以对于同样的缺失率${\gamma }_0$，$1?{\gamma }^2>1?\gamma$， 所以对缺失的惩罚会变小，即是削弱的。

【练习4】如果将树的生长策略从深度优先生长改为广度优先生长，假设其他参数保持不变的情况下，两个模型对应的结果输出可能不同吗？

可能会。因为有max_leaf_nodes这个限制。在达到max_leaf_nodes的限制之后，如果按照深度优先搜索来的话，则会有很多节点在max_depth处是叶子节点；当采用广度优先搜索的话，则当达到max_leaf_nodes限制之后，可能会在1/2 max_depth时停止分裂。采用深度优先搜索得到的树在深度「比较大」的概率会比较大，而又因为在深度比较大的叶节点上，它分类的准确率又是比较高的，所以我认为会不同。

【练习5】在一般的机器学习问题中，我们总是通过一组参数来定义模型的损失函数，并且在训练集上以最小化该损失函数为目标进行优化。请问对于决策树而言，模型优化的目标是什么？

使得子树的不纯度尽可能小。不纯度低意味着纯度高，一个叶子节点中实际的类别数量是比较少的，并且确定性是比较高的。

【练习6】对信息熵中的$log$?函数在$p=1$?处进行一阶泰勒展开可以近似为基尼系数，那么如果在$p=1$?处进行二阶泰勒展开我们可以获得什么近似指标？请写出对应指标的信息增益公式。

泰勒展开式为
$$f(x)=f(x_0)+f^{{}^{\prime }}(x_0)\frac{(x?x_0)}{1!}+f^{{}^{\prime \prime }}(x_0)\frac{(x?x_0{)}^2}{2!}+?+f^n(x_0)\frac{(x?x_0{)}^n}{n!}+O((x?x_0{)}^n)$$
故$\ln x$在$p=1$处的二阶泰勒展开式为
$$\begin{array}{rl}\ln x& \approx \ln 1+\frac{1}{1}\frac{x?1}{1}?\frac{1}{1^2}\frac{(x?1{)}^2}{2}\\ & =x?1?\frac{1}{2}(x?1{)}^2\\ & =?\frac{1}{2}{x}^2+2x?\frac{3}{2}\end{array}$$
故信息熵中的$\log$?函数在$p=1$??处进行二阶泰勒展开为：
$$\begin{array}{rl}{\mathbb{E}}_Y[?\log Y]& ={\mathbb{E}}_Y[\frac{3}{2}?2Y+\frac{1}{2}{Y}^2]\\ & =\sum _{k=1}^K\tilde{p}(y_k)[\frac{3}{2}?2\tilde{p}(y_k)+\frac{1}{2}{\tilde{p}}^2(y_k)]\\ & =\frac{3}{2}?2\sum _{k=1}^K{\tilde{p}}^2(y_k)+\frac{1}{2}{\tilde{p}}^3(y_k)\end{array}$$
【练习7】除了信息熵和基尼系数之外，我们还可以使用节点的$1?{\max }_{k}p(Y=y_k)$???和第m个子节点的$1?{\max }_{k}p(Y=y_k|X=x_m)$??来作为衡量纯度的指标。请解释其合理性并给出相应的信息增益公式。

合理性：当${\max }_{k}p(Y=y_k)$?等于1时，纯度为0，概率为1，随机事件发生，我们就很容易猜到它可能是这个概率为1的事件，这显然是合理的。而且${\sum }_{k=1}^K{p}_k=1$?保证纯度取值在$[0,1]$?之间。

TODO: 补充信息增益公式。

信息增益公式为：
$$\begin{array}{r}G(Y,X)\end{array}$$

【练习8】为什么对没有重复特征值的数据，决策树能够做到损失为0？

因为对于没有重复特征的数据，比如所这个所有的特征都是离散特征且特征是不重复的，所以我们总能够对这个特征有限次分裂（对这个特征的每个分类点都进行分裂），最后会得到对于每个特征的不同组合得到一个叶子节点，每个样本点都会被分配到其中的一个节点，最后所有的特征都被分类正确。

【练习9】如何理解min_samples_leaf参数能够控制回归树输出值的平滑程度？

min_samples_leaf最大的作用在于控制叶节点的数量，使得它不过分大（大于min_samples_leaf) 。取两个极端情况来看，当min_sample_leaf为1时，最后叶子节点的数量为N(样本数量)，最后输出样本的方差为原始数据集的方差；当min_samples_leaf为N时，根节点不进行分裂，但是此时输出值为所有因变量$Y$?的均值，得到的方差为原始方差的1/N, 也就更加光滑。而当min_samples_leaf取值1和N之间时，方差介于两者之间，当min_samples_leaf值比较小时，光滑程度比较大，当min_samples_leaf比较大时（靠近N），光滑程度比较小，取值相对凹凸不平一些。

知识回顾

1. ID3树算法、C4.5树算法和CART算法之间有何异同？

   • ID3, C4.5只能用于分类，而CART不仅可以分类，还可以进行回归

   • ID3使用的信息增益作为分裂节点的准则，C4.5用信息增益比来分裂节点；CART在分类时可以用Gini指数来分裂节点，在回归时，可以使用MSE和MAE来分裂节点

   • C4.5在处理数值特征时，可以使用最佳分割法和随机分割法，而ID3只有最佳分割法；

   • C4.5 可以处理缺失数据，对缺失数据进行惩罚，而ID3不行

   • ID3, C4.5 只生成树，不剪枝，容易过拟合；但是CART会对生成的树进行剪枝。

2. 什么是信息增益？它衡量了什么指标？它有什么缺陷？

   信息增益是，节点分裂之后信息熵减少的量，它衡量了节点分裂之后不确定性的的降低或者而纯度的提高。

   缺陷：特征取值多的信息熵比较大，信息增益也比较大。在决策树使用信息增益比来进行节点分裂时，会比较倾向于取值比较多的特征，这会对树的预测精度造成影响。

   解决：使用信息增益比可以降低对取值较多的特征的关注。

3. sklearn决策树中的random_state参数控制了哪些步骤的随机性？

   • 选取max_features进行分裂时，选取的特征
   • 决策树生长时，找到下一个分裂节点，使用的是深度有限生长时，找到一个节点进行深度优先生长时，所选择的那个节点

4. 决策树如何处理连续变量和缺失变量？

   从连续变量的最大最小值中找到一个值来切分变量，使得这个变量变成分类变量，在分割点左边的为一类，在分割点右边的为一类；

   处理缺失变量：计算剩下特征中非缺失值的信息熵，计算缺失值的比例$\gamma$, 用$1?\gamma$ 乘以计算得到的信息熵

5. 基尼系数是什么？为什么要在CART中引入它？

   基尼指数是衡量一个节点分裂之后得到的信息增益，其计算如下：
   $$Gini(Y)=1?\sum _{k=1}^K{\tilde{p}}^2(y_k)$$
   其中$\tilde{p}(y_k)$是利用样本计算得到$y_k$出现的频率，估计的$y_k$出现的概率。

   引入它，是因为之前计算的信息增益中的对数$log$不好计算，所以找到了$log$函数在$p=1$处的近似值。

6. 什么是树的预剪枝和后剪枝？具体分别是如何操作的？

   预剪枝：在判断节点是否分裂的时候就通过一些规则来阻止其分裂.

   后剪枝：在数的节点已经全部生长完成后，通过一些规则来摘除一些子树。

   后剪枝步骤

   1. 计算当前节点为根节点的树的剪枝度量
      $$R_{\alpha }(T^N)=R(T^N)+\alpha |T^N|$$

   2. 计算当前节点不分裂时的剪枝度量:
      $$R_{\alpha }(Nod{e}^N)=R(Nod{e}^N)+\alpha$$

   3. 如果一个根的剪枝度量小于其子节点的剪枝度量的话，即
      $$R_{\alpha }(T^N)\le R_{\alpha }(Nod{e}^N)$$
      此时有$\frac{R_{\alpha }(Nod{e}^N)?R(T)}{|T^N|?1}\le \alpha$

   4. 从叶子节点往根节点，按照1-3来计算与判断，直到不能够进行剪枝为止。

   TODO: 补充预剪枝过程。