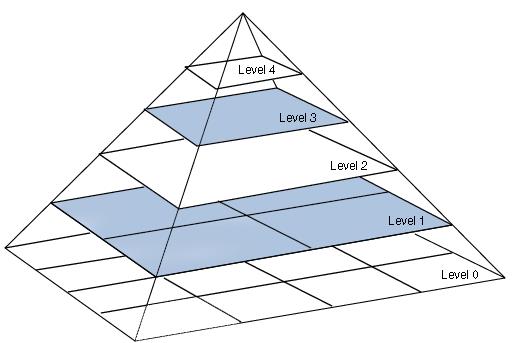
? ? ? ? ? ? ? ? 图像“金字塔”是通过多个分辨率表示图像的一种有效且简单的结构,它是以一系列以金字塔形状排列、分辨率逐步降低的图像集合,如图:
?一、高斯“金字塔”
? ? ? ? 它是解决尺度不确定性的一种常用的方法。它是指通过下采样不断地将图像的尺寸缩小,进而包含多个尺寸的图像。通常情况没往上一层,尺寸缩小为原来的一半。在OpenCV中提供了pyrDown()函数专门用于图像的下采样的计算。
pyrDown()函数原型:
void cv::pyrDown(InputArray src,
OutputArray dst,
const Size & dstsize = Size(),
int borderType = BORDER_DERAULT
)src:输入待下采样的图像。
dst:输出下采样后的图像,图像尺寸可以指定,但是数据类型和通道数与src相同。
dstsize:输出图像尺寸,可以默认。
borderType:像素边界外推方法的标志。
? ? ? ? 该函数实现图像模糊并对其进行下采样,我们可以通过dsize参数来设置输出图像的大小,无论尺寸多大都满足下式。该函数首先将原始图像与内核矩阵进行卷积,内核矩阵如下,之后通过不使用偶数行和列的方式对图像进行下采样。
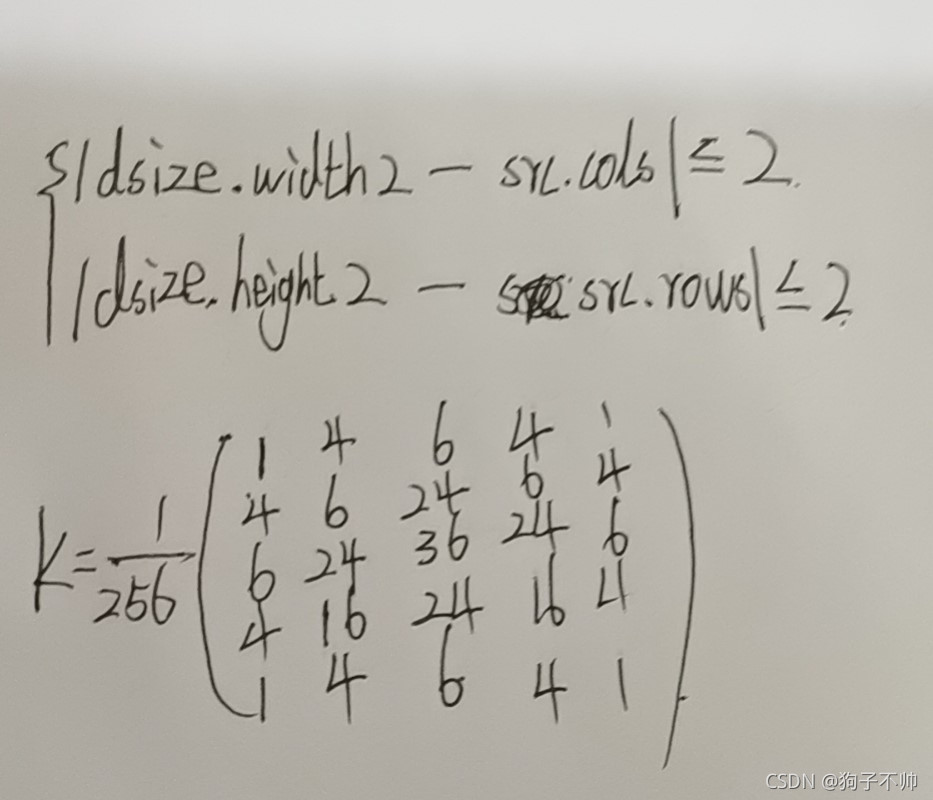
?二、拉普拉斯“金字塔”
? ? ? ? 拉普拉斯“金字塔”与高斯“金字塔”相反,高斯“金字塔”通过底层图像构建上层图像,而拉普拉斯“金字塔”通过上层小尺寸的图像构建下层大尺寸图像。拉普拉斯“金字塔”具有预测残差的作用,需要与高斯“金字塔”联合使用。假设我们已经有一个高斯图像“金字塔”,对于其中的第i层图像,首先通过下采样得到一个尺寸缩小一半的图像,即高斯“金字塔”中的第i + 1层或者不在高斯“金字塔”中,之后通过对这幅图像进行上采样,将图像的尺寸恢复到第i层图像的大小,最后求取高斯“金字塔”第i层图像与经过上采样后得到的差值图像,这个差值图像就是拉普拉斯“金字塔”的第i层图像。
? ? ? ? 对于上采样在OpenCV中提供了pyrUp()函数,函数原型如下:
void cv::pyrUp(InputArray src,
OutputArray dst,
const Size& dstsize = Size(),
int borderType = BORDER_DEFAULT
)?实例代码如下:
#include<opencv2/opencv.hpp>
#include<iostream>
#include<vector>
using namespace std;
using namespace cv;
int main()
{ int i = 0;
Mat img = imread("f9afe18da2fb1fa2ff72c4d8b29fe6a (2).png");
if (img.empty())
{
cout << "请检查文件的名字是否正确" << endl;
return -1;
}
vector<Mat> Gauss, Lap; //高斯金字塔,拉普拉斯金字塔
int level = 3; //下采样的次数
Gauss.push_back(img); //将原图作为高斯金字塔的第零层
for (int i = 0; i < level; i++)
{
Mat gauss;
pyrDown(Gauss[i], gauss);
Gauss.push_back(gauss);
}
//构建拉普拉斯金字塔
for (int i = Gauss.size() - 1; i > 0; i--)
{
Mat lap, upGauss;
if (i == Gauss.size() - 1)//如果是高斯金字塔的最上面一层图像
{
Mat down;
pyrDown(Gauss[i], down);
pyrUp(down, upGauss);
lap = Gauss[i] - upGauss;
Lap.push_back(lap);
}
pyrUp(Gauss[i], upGauss);
lap = Gauss[i - 1] - upGauss;
Lap.push_back(lap);
}
for (int i = 0; i < Gauss.size(); i++)
{
string name = to_string(i);
imshow("G" + name, Gauss[i]);
imshow("l" + name, Lap[i]);
}
waitKey(0);
return 0;
}