李宏毅机器学习Task03
本次任务依旧关注回归问题,涉及到一些概率和微积分的内容,大体上都能听懂在讲些什么。
误差
误差有两个来源:偏差与方差。
偏差
偏差描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距,简单讲,就是在样本上拟合的好不好。要想在偏差上表现好,就要将模型变得复杂一些,增加参数,但是这样容易过拟合。
偏差大的时候,我们首要考虑的问题就是去改进自己的模型,以宝可梦为例就是除了进化前的CP值,还要考虑一些高度重量等数据,此时去收集更多的数据其实意义并不大。
方差
方差描述的是样本上训练出来的模型在测试集上的表现,要想在方差上表现好,就要简化模型。但是这样容易欠拟合。
方差大了,我们的方法比较简单粗暴,就是可以获取更多的数据,不过很多时候无法手机到更多的数据,此时可以针对问题理解对数据集做调整。
模型的选择
根据课上内容,我个人理解偏差和方差在都是尚可的模型中是一对矛盾,我们的任务在于找到一个平衡点,能够同时得到较低的偏差与方差,使得最后误差最小。

在选择模型的时候,不要简单的认为在自己手头的测试集中表现最好的模型就是实际上最好的模型,其实由于你并没有真实的测试集,你的模型究竟如何并不清楚。
所以我们通常会多做几步来解决这个问题,课程中提供了一种交叉验证的方法。
交叉验证
交叉验证就是将训练集分为两部分,一部分作为训练集,一部分作为验证集。用训练集训练模型,然后再验证集上比较,确实出最好的模型之后(比如模型3),再用全部的训练集训练模型3,然后再用public(手头上)的测试集进行测试。不推荐利用测试集的数据再去调模型来让误差更小。
n折交叉利用
考虑道单次分组有偶然性,我们可以多次分组。
将已有的训练集中的数据多次分组,每组可以有两部分来训练,一部分来验证,这样每一组我们都能得到一个误差可以用各个模型在所有组的表现取一个均值,最后取得一个误差均值最小的模型。
再谈梯度下降
上次任务中我们已经接触过梯度下降的方法,梯度下降就是找出模型中最合适的参数,本次课程中扩充了相关知识。
梯度下降的数学原理
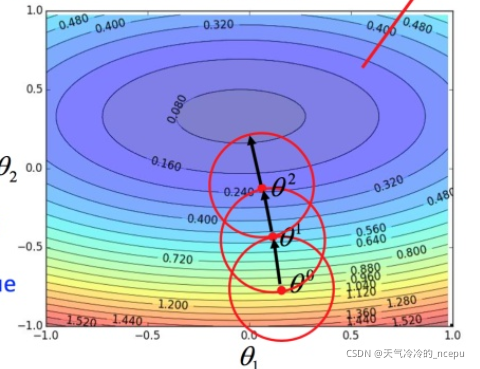
实际上我们要做的工作是先随机取一个点,然后画一个圈,在这个圈内去找损失函数最小的点,以找到的点再画圈找点,反复工作。最后就可以将损失函数的最小值找到。
那么问题的关键就在于如何找到损失函数值最小的点。
泰勒展开法
泰勒展开是高数中学过的知识,记得当时被折磨的厉害,这里不再复述。
我们可以在圈内将损失函数泰勒展开一下(略去后面的高阶项):
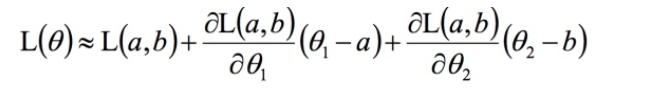
考虑让值最小,第一项为常值,实际上就是后两项越小,也就是两个向量(△θ1,△θ2 ) 和 (L关于θ1偏导,L关于θ2偏导) 的内积最小,方法就是两个方向相反。
到最后就可以推出梯度下降的公式。
这里用这种方法找到这个式子有个前提,泰勒展开式给的损失函数的估算值是要足够精确的,而这需要红色的圈圈足够小(也就是学习率足够小)来保证。这也与之前的试验中要保证小学习率的推测比较符合。
如果我们考虑泰勒公式中的二阶项,会发现多了很多运算,结果上差异也不大,所以基本都是一阶搞定。
学习率的取法
通过原理分析与之前的实践,我们能够看出学习率值是一个非常关键的参数,直接关系到能否找到那个f*。
Adagrad自适应算法
每个参数的学习率都把它除上之前微分的均方根。
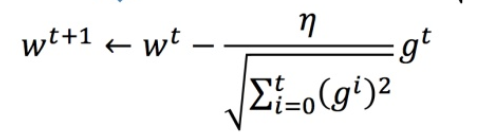
Adagrad的问题
在 Adagrad 中,当梯度越大的时候,更新的值应该更大,但下面分母又导致梯度越大的时候,更新的值会越小。
问题解释
李老师用了一个二次函数的例子开始,我们发现如果算出来的微分越大,则距离最低点越远。而且最好的下次更新的值的大小和一阶导正比。最佳距离:
∣
2
a
x
0
+
b
2
a
∣
|\frac{2ax_0+b}{2a}|
∣2a2ax0?+b?∣
同时发现在多参数下结论不成立。
同时观察到一元情况下分母的2a正是函数的二阶导,即不止和一次微分成正比,还和二次微分成反比。
一
次
微
分
二
次
微
分
\frac{一次微分}{二次微分}
二次微分一次微分?
最好的步骤应该考虑到二次微分。对于
∑
i
=
0
t
g
i
2
\sqrt{\sum_{i=0}^{t}g_i^2}
∑i=0t?gi2?? 就是希望在尽可能不增加过多运算的情况下模拟二次微分。
随机梯度下降法
损失函数不需要处理训练集所有的数据,选取一个例子
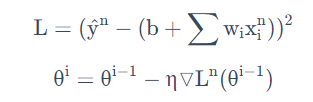
此时不需要像之前那样对所有的数据进行处理,只需要计算某一个例子的损失函数,就可以赶紧更新值。
特征缩放
假如输入的分布的范围很不一样,建议把他们的范围缩放,使得不同输入的范围是一样的。
特征缩放是在多元的情况下考虑,在两个输入分布的范围差距很大时,对应的参数影响损失函数效果就会不同,这种情况不是我们想要的。
特征缩放的方法很多,本次课程入门性质,具体方法有待后续的深入学习。