本篇笔记包含学习章节:
P5误差从哪来
P6梯度下降
P7梯度下降(用AOE演示)
P8梯度下降(用Minecraft演示)
目录
一、误差的来源
error来自于bias和variance。关于偏差和方差的认识可以从射箭的例子来理解。

?图源 知乎?既生宇何生亮 ?的回答
?机器学习中的 Bias(偏差)、Error(误差)、Variance(方差)有什么区别和联系? - 知乎
模型的复杂度越高,偏差越小,方差越大。因此在模型的选择中,偏差和方差的权衡是一个重要的问题。大偏差小方差,是欠拟合;大方差小偏差,是过拟合。

遇到欠拟合时,考虑函数是不是设置错误了,可以将更多的函数加进去,比如考虑高度重量,或者HP值等等。 或者考虑更多次幂、更复杂的模型。?
遇到过拟合时,可以加入更多的数据,或者是对数据集进行调整。
由于测试集往往是一开始我们拿不到的,为了控制测试误差,交叉验证是很重要的方法。
(一)验证集方法
随机将观测数据对半分为训练集和验证集。
优点:易于操作
缺点:测试误差预测误差大;观测数据少,可能导致高估测试错误率。
(二)k折交叉验证
将数据随机分成k份,分别将第1,2...,k折作为验证集,在剩下的k-1折上拟合模型。计算出的k个测试误差求均值得到最终的估计值。
k折交叉验证得到的测试误差的波动会比验证集方法要小得多。
模型选择:选择平均测试误差最小的模型,再用全部训练集训练模型。
二、梯度下降
(一)学习率的选择
(1)手动调整
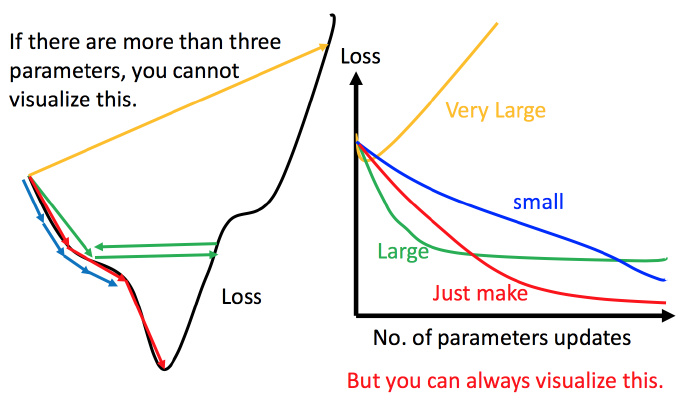
学习率的选择非常重要,如果学习率调整的刚刚好,就能顺利找到最低点。如果学习率调整的太小,就会走的太慢,实际情况可能会等不及出结果。如果学习率调整的有点大,就会在上面震荡,走不下去,永远无法到达最低点。甚至直接就“飞”出去了,损失函数越更新越大。如下左图是比较直观的显示,但是一旦多于三个参数便很难可视化。
可以使用另一种可视化方法来选择学习率,将参数改变对损失函数的影响进行可视化。如下右图所示。
(2)自适应学习率
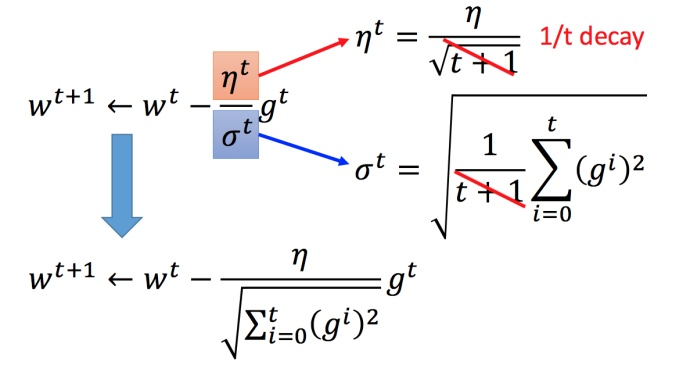
举一个简单的思想:随着次数的增加,通过一些因子来减少学习率,比如随着迭代次数的增加缩短步长:
但是对于不同的参数采用相同的步长也是不合理的,所以我们考虑给不同参数不同的学习率
(3)Adagrad算法
在学习率的计算中加入不同参数的信息:
每个参数的学习率都把它除上之前微分的均方根。学习率的更新可以参照下图中的例子:
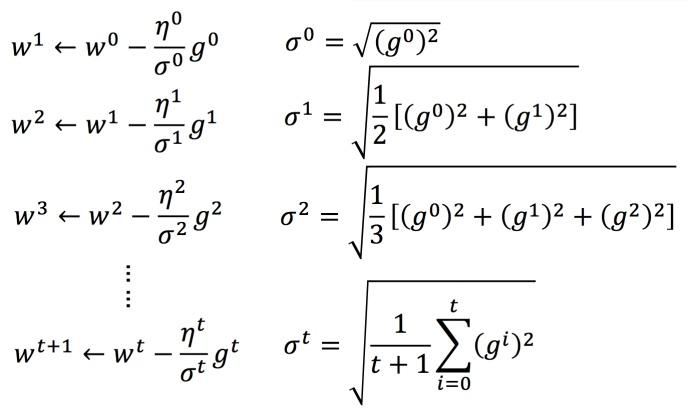
这个时候我们想要从直观去理解,微分值如果变化不大的话,学习率也不会发生大的变化。
但是Adgrad似乎存在一个问题:如果微分值突然减小,意味着下降的斜率减缓,则需要减缓学习率,然而Adgrad更新的学习率却变大了。
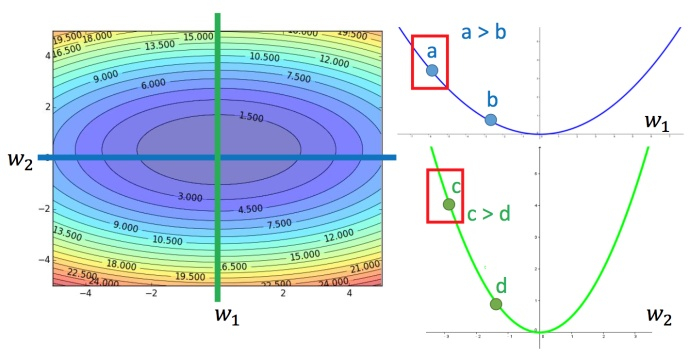
李宏毅老师的解释是,“梯度越大,就跟最低点的距离越远。”单个参数这么想是对的,但是多变量下时,跨参数对比之下,最优的步长不能只考虑一阶微分,还得考虑二阶微分才行。如下图所示,比较最优学习率,只考虑w1,a比b大;只考虑w2,c比d大。但同时考虑w1和w2,则需要考虑两个函数的二阶微分值。
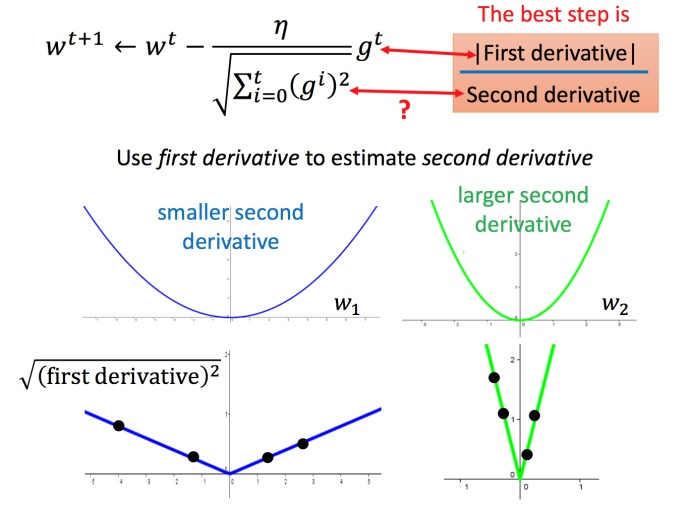
如下图所示,事实上,的最优学习率可以写成一阶微分/二阶微分的形式。
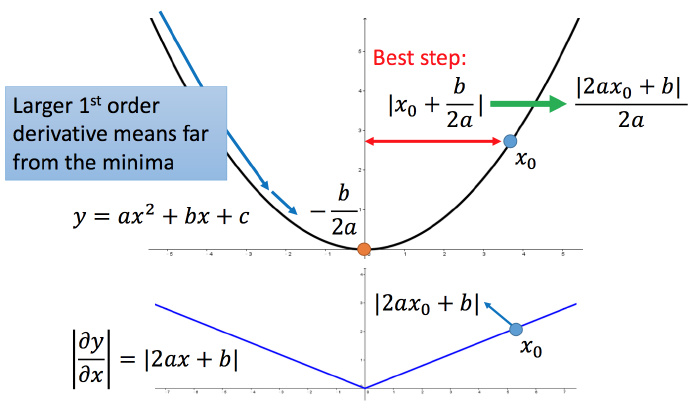
?而Adgrad事实上是同时考虑到了一阶微分和二阶微分的。这里的由于是对单个参数而言的,并不代表下降方向,而代表一阶微分,分母实际上是用一阶微分来估计二阶微分(包含了二阶微分的信息)
?(4)随机梯度下降法
随机梯度下降法有更快的更新速度。Loss函数只考虑一个样本,并立刻更新参数。会比梯度下降法快很多!(但我不知道它的准确性怎么样。可以通过实践来比较)
(5)特征缩放
输入的分布的范围差异很大时,把他们的范围缩放,使得不同输入的范围是一样的。

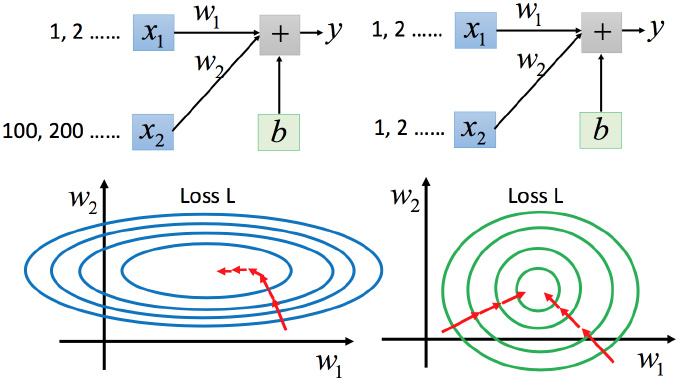
?为啥呢?如下图所示,x1??的scale比 x2??要小,所以当 w1??和 w2??做同样的变化时,w1??对?y 的变化影响更小。考虑两个参数的error surface,左边蓝色图中表现了scale差距大时,沿梯度方向下降的方向不是向着最低点的方向,需要不断更新,而且两个方向需要不同的学习率,因此需要Adagrad。右边的绿色图是scale比较接近的示意图,更新参数的方向一开始就可以向着最低点,这样做参数更新更有效率。
?做法一般是类似于做标准化处理。(减去均值,除以标准差)
(二)梯度下降法的数学基础
对损失函数进行泰勒展开。
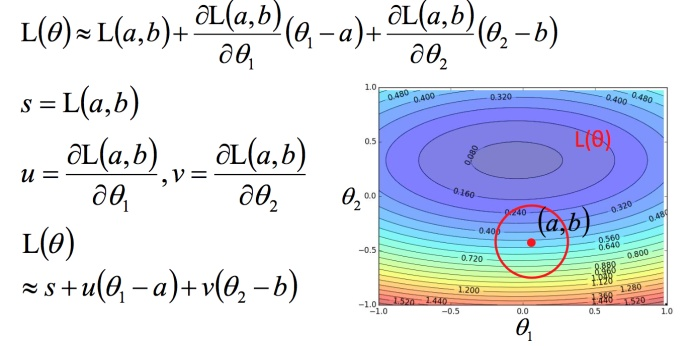

问题转化为最小化两个向量()和 (
)?的内积,即与向量 (
)??方向相反的向量


?泰勒展开式的使用要求红色的圈圈足够小,也就是学习率足够小
所以实际中,当更新参数的时候,如果学习率没有设好,会导致做梯度下降的时候,损失函数没有越来越小。
(三)梯度下降的限制:局部最优
参考教材:An introduction to statistical learning