频域滤波步骤:
1.给定大小为 M × N M\times N M×N的输入图像,将其填充为大小 P × Q P\times Q P×Q的图像其中 P = 2 M , Q = 2 N P=2M,Q=2N P=2M,Q=2N。填充方法为:在M,N的后面添加0(尾部加0)。设经过此步骤的图像为 f p ( x , y ) f_p(x,y) fp?(x,y)
进行第一步的原因(下面卷积公式应为f(m)):
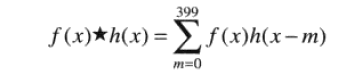
如图,相当于对h(m)关于y轴对称之后向右不断平移x,并求其和f(m)的乘积。如果对称之后,h(m)的图像与h(x) or f(x)有重叠,就会产生混叠,影响结果。

2.对图像× ( ? 1 ) x + y (-1)^{x+y} (?1)x+y,将其移到变换中心
进行第二步的原因:

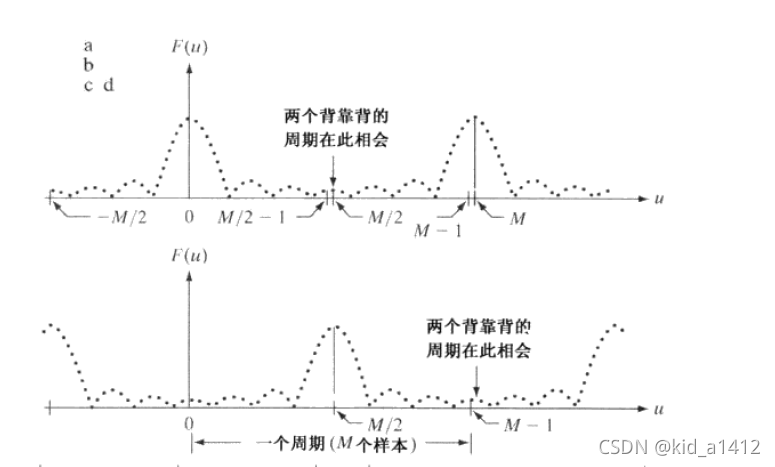
如图,进行运算之后在
[
0
,
M
?
1
]
[0,M-1]
[0,M?1]内是完整的一个周期,便于DFT
3.计算步骤二之后获得的图像(矩阵)的DFT
就直接套公式就完事了
F
(
u
,
v
)
=
∑
x
=
0
M
?
1
∑
y
=
0
N
?
1
f
(
x
,
y
)
e
?
2
π
j
(
u
x
M
+
v
y
N
)
F(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-2\pi j(\frac{ux}{M}+\frac{vy}{N})}
F(u,v)=∑x=0M?1?∑y=0N?1?f(x,y)e?2πj(Mux?+Nvy?)
4.生成一个实的,对称的滤波函数H(u,v),其大小为P×Q,中心在(P/2,Q/2)处,G(u,v) = H(u,v).*F(u,v)
要注意滤波函数的生成大小,低通滤波器可以用
%D(u,v)<=D0时有值
u = 0:Q-1
v = 0:P-1
%calculate D(u,v)
H = double(D<=D0)
控制滤波器的大小
5.对G进行傅里叶反变换,得到g(x,y),并对其取实部,乘(-1)^(x+y)

其实取abs实际感觉差别不是很大
6.从g(x,y)上提取M*N的部分得到最终结果。
下面是代码实现
%matlab调库
function [DFT_img] = FFT_(I,H)
%调用FFT库函数实现频域滤波
%输入 I为图像f(x,y),H为滤波器H(u,v)
%输出滤波后的图像g(x,y)
%在不严谨的情况下我们可以不做扩展0,结果仍然与正确结果差不多
F = fft2(I);
Fs = fftshift(F);
out = H.*Fs;
out=ifftshift(out);
out=ifft2(out);
out=real(out);%用abs基本没区别
out=out/max(out(:));%除以out中最大值
DFT_img = out;
end
%以低通滤波为例
path = 'your own path';
I = imread(path);
M = size(I,2);
N = size(I,1);
u=0:M-1;
v=0:N-1;
[U,V]=meshgrid(u,v);%基于向量 x 和 y 中包含的坐标返回二维网格坐标
D=sqrt((U-M/2).^2+(V-N/2).^2);
D0=15;%截止频率
H=double(D<=D0);%理想低通滤波器
n = FFT_(I,H)
imshow(n,[])%不加[]效果相同
原图:
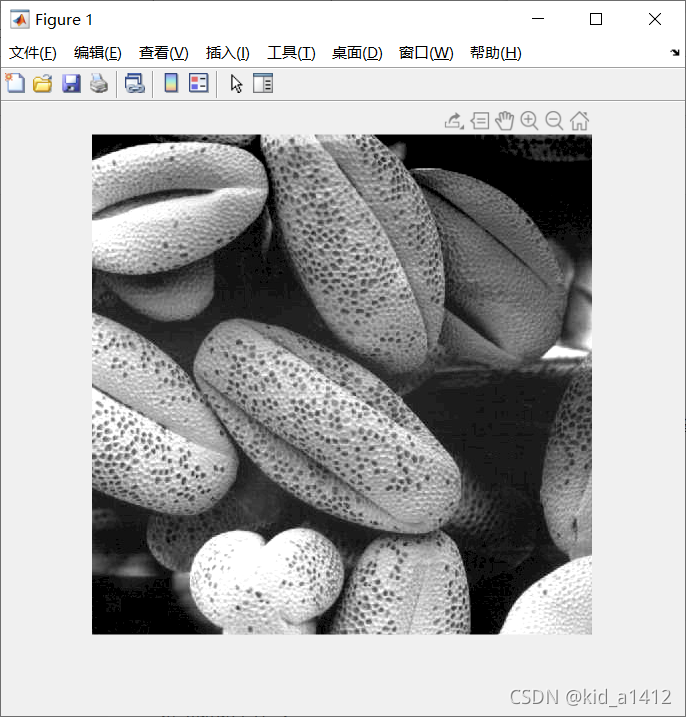
低通滤波以后(D0=15):
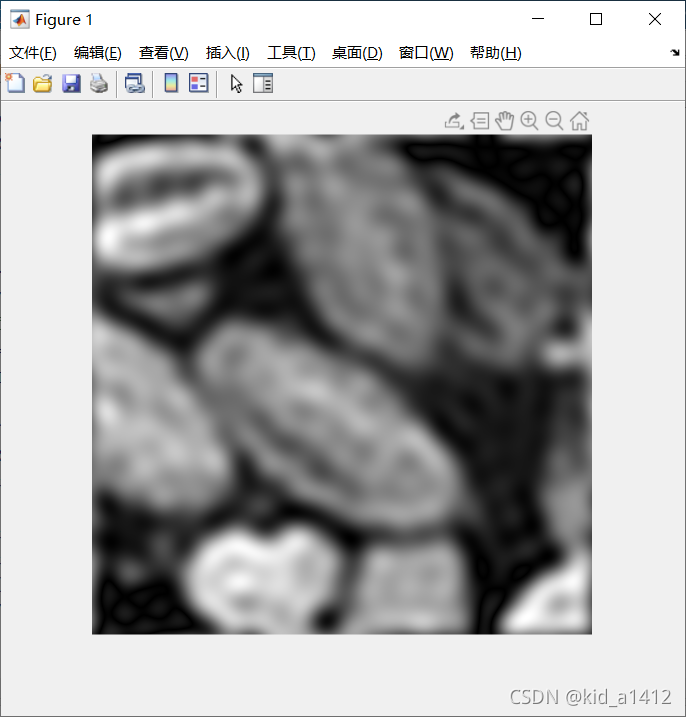
若D0=5,可以看到更为模糊的图像:
matlab库函数解析:
-
Y = fft2(X)——输出X的二维傅里叶变换
Y = fft2(X,m,n) 将截断 X 或用尾随零填充 X,以便在计算变换之前形成 m×n 矩阵 -
fftshift(X)将零频分量移到屏幕中心,相当于我们上述讲的 × ( ? 1 ) x + y \times(-1)^{x+y} ×(?1)x+y
实际上fftshift操作的时候就是把矩阵X第一象限与第三象限交换,第二象限与第四象限交换。(相当于拆开再拼起来) -
ifftshift(X) 撤销fftshift(X)的结果,实际还是第一象限与第三象限交换,第二象限与第四象限交换。
-
ifft2(X) 二维傅里叶逆变换