Gamma映射原理
- 什么是Gamma曲线
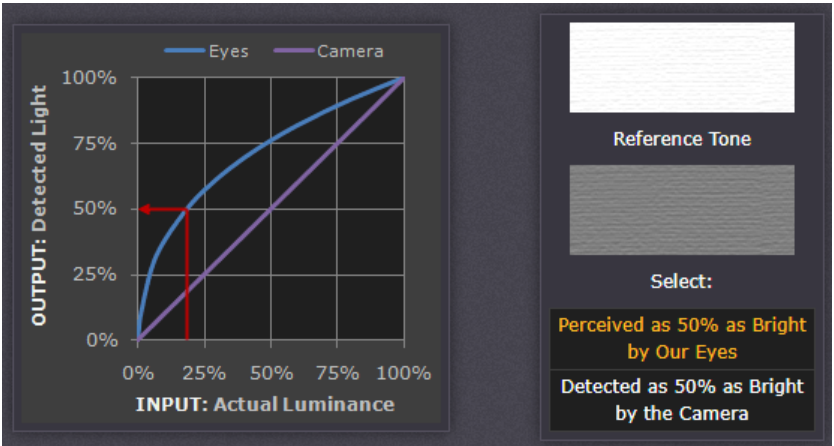
人眼的感光与光强并不是呈线性关系的,而是呈非线性关系(指数型关系,如下图左-曲线。在低照度下,人眼更容易分辨出亮度的变化,随着照度的增加,人眼不易分辨出亮度的变化。而图像传感器与输入光强呈线性关系(如下图左-直线)。从图中可见,当传感器感光在20%左右时,人眼感光响应达到了50%,人眼对低照度的变化更为敏感。从下图右侧可见,Reference Tone为人眼感光50%的亮度,而传感器在感光50%时则相对暗的多(见Select,近似中性灰)。这种将原始图像通过映射操作来满足人眼亮度响应的曲线,就是Gamma曲线,响应的变换就是Gamma变换。
?
?
光有曲线的数据,虽已具象化,但没有感性的认识,着实不太好理解。我们举个例子,你在黑暗的夜晚,草丛有一只微弱的萤火虫,你会敏锐的发现,或是远方灯火阑珊,那更是灵光一现;但倘若在大白天,从早上8点到正午12点,虽阳光逐渐变得强烈,你却没有很直观的变化。所以可以理解人眼在低照度时候,对亮度的变化更为敏感,而在高亮时却不是很灵敏。
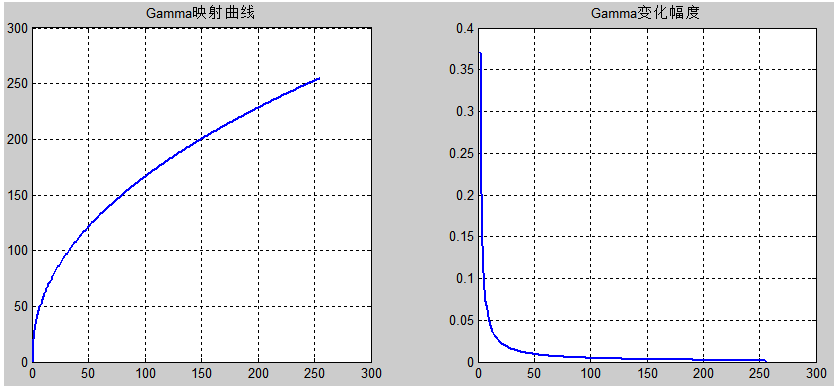
换个维度,假设在Gamma曲线上(以Gamma=2.2为例),我们计算亮度变化的幅度,即我们8bit图像亮度为0-255灰阶,映射到Gamma曲线后,则从灰阶1到2亮度变化幅度为37.04%,但从灰阶幅度254到255,亮度变化则仅只有0.18%,曲线如下图所示:
?
其中相关代码如下所示:
% -------------------------------------------------------------------------
% Gamma映射函数
x = [0:1:255];
y1 = (255/255.^(1/2.2))*x.^(1/2.2);
y2 = zeros(1,256);
for i = 1:255
if(x==0)
y2(1)=0;
else
y2(i)=(y1(i+1)-y1(i))/y1(i);
end
end
subplot(121),plot(x,y1,'Linewidth',2);grid on; title('Gamma映射曲线');
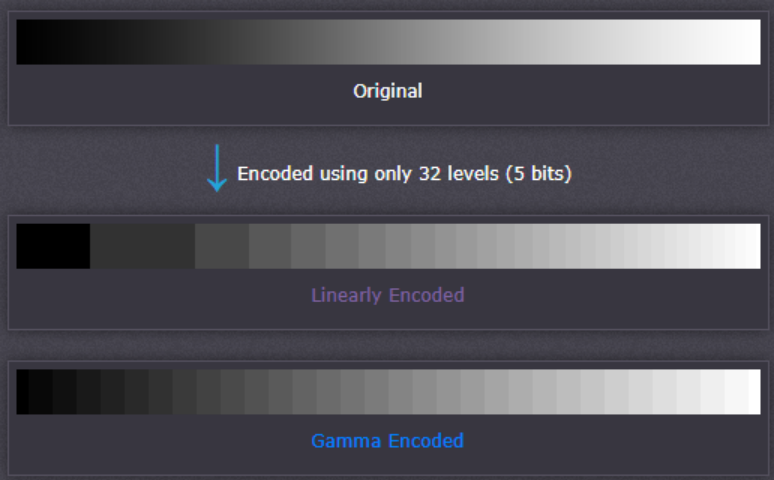
subplot(122),plot(x,y2,'Linewidth',2);grid on;title('Gamma变化强度');那么,不管从生活还是数据中分析,在高亮下人眼对光强不敏感,而在低照度下更敏感,因此足以见得Gamma映射的重要性。所以在ISP流程中,Gamma是很重要的一部分,我们为了适合人眼进行辨识,对图像传感器产生的图像进行Gamma变换,来提升图像的辨识度。如下图所示,为原始图像经传感器采集的未经Gamma变化的灰阶图(Linear Encoding),以及经过Gamma变换后的灰阶图(Gamma Encoding)。
?
从图中可见,在未经过Gamma变换时,低灰度值区域在较大范围内表现为同一个值,造成信息的丢失;同时高灰度值区域又被表现为很多不同的值,造成存储的浪费。但经过Gamma变换后,低灰度值下有了更多的灰阶信息,而高灰度值下进行了一定程度的压缩,节省了图像的存储。
- Gamma为啥是2.2
这事我不一定说的准确,仅凭个人卓见,两方面给大家阐述一下。
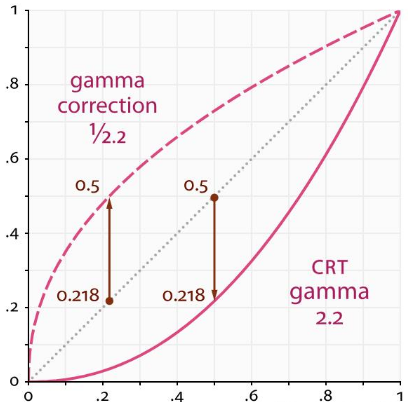
首先是当年的大脑袋的CRT显示器(00后不知道有没有见过),由于其显像管与电压并不是成线性关系。如下图所示,CRT亮度响应曲线。从曲线可知其暗区被压缩了(斜率小于45°),而亮区则被扩展了(斜率大于45°)。典型的比如输入40%亮度的红色+80%亮度的绿色,实际输出近似10%的红色+60%的绿色,显示严重不及预期。
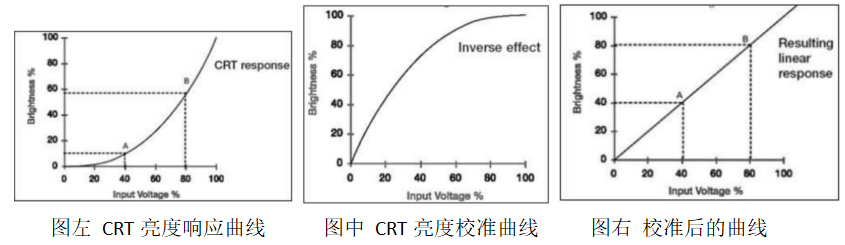
为了弥补这一亮度响应的缺陷,我们需要一个反转的曲线,如上图中间曲线所示。经过中间反转曲线的抵消,最终达到预期的亮度,将会出现上图右边的曲线:近似45°斜率的直线,即便输入和亮度成正比关系,而这一亮度补偿的映射,就是Gamma,CRT的Gamma值据统计分析就在2.2左右。Gamma值没有标准,也没有对错,比如CRT有些文档说2.5,Windows系统默认Gamma=2.2,而Mac系统的Gamma又是1.8,不同的LCD屏幕响应曲线各有不同,最正确的方法则是通过灰阶自己找到最佳的Gamma值。
目前经典的Gamma值就是2.2,或许这是一种巧合,但这也是一个现实,从大量的人眼视觉特性中统计分析出一个经验值,我们人眼的亮度响应曲线,也刚好是2.2。
综上,CRT的亮度响应是一条Gamma曲线(往下弯),CRT的亮度补偿是一条反Gamma曲线(往上弯),而人眼的亮度响应也是一条反Gamma曲线,因此为了达到更好的亮度与对比度,符合人眼的视觉效果,需要额外的反Gamma曲线去对画面进行细微的明暗层次调整,控制整个画面对比度表现,再现立体美影像。
备注:第一次,我们叫作Gamma矫正,第二次个人认为只能称之为Gamma映射。那么既然是映射,跟对比度增强映射也就是一个道理了。
-
- 如何进行Gamma变换
Gamma来龙去脉很复杂,但实现却很简单,只是简单的Mapping操作,是对输入图像灰度值进行的非线性操作,使输出图像灰度值与输入呈指数关系,公式如下:

?这个指数系数就是Gamma变换的系数。Gamma变换后,提升了暗部细节,压缩了亮部细节(Gamma<1);或者提升了亮部细节,压缩了暗部细节(Gamma>1)。如下图中,下方实曲线为CRT的Gamma曲线,而上方虚曲线则为矫正CRT亮度响应的曲线,校正后使得最终近似斜率为45°的线性响应(Gamma=1)。但事实上显示器已经自带了虚曲线的Gamma矫正曲线,其输入与输出在校正后已近似线性,但为了能够让图像变得更加接近人眼感受的非线性响应,提升图像显示的质量,我们仍然可以进一步Gamma 2.2的映射。
?
上图为官方的图,其中最下方为CRT Gamma 2.2的曲线,而最上方则为反Gamma曲线。由于我们在PC侧处理的像素都是0-255,那么对公式进一步变型,扩展到0-255,计算如下:

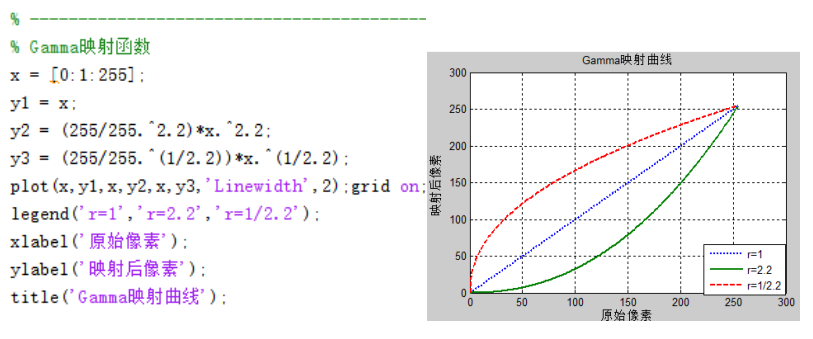
??使用Matlab绘制的如上曲线,如下所示。我们将始终在0-255之间,进行线性响应的非线性拉伸,来符合人眼/设备的响应曲线。
?
- Gamma映射Matlab实现
首先申明:这里只是演示Gamma映射的算法,但结果并没有对错,毕竟原图可能已经优化过,同时也可能因人而异。
前面已经用Matlab绘制过Gamma曲线,这里为了观察效果,我们同时绘制Gamma=2.2及Gamma=1/2.2的映射结果,以及前一篇中对比度增强的效果,来提高你对曲线映射图像处理的认知。如下所示为Matlab源代码:
% -----------------------------------------------------------------------
% \\\|///
% \\ - - //
% ( @ @ )
% +---------------------------oOOo-(_)-oOOo-----------------------------+
% CONFIDENTIAL IN CONFIDENCE
% This confidential and proprietary software may be only used as authorized
% by a licensing agreement from CrazyBingo (Thereturnofbingo).
% In the event of publication, the following notice is applicable:
% Copyright (C) 2013-20xx CrazyBingo Corporation
% The entire notice above must be reproduced on all authorized copies.
% Author : CrazyBingo
% Technology blogs : www.crazyfpga.com
% Email Address : crazyfpga@qq.com
% Filename : Image_Constrast.m
% Date : 2021-08-25
% Description : Image Constrast alg.
% Modification History :
% Date By Version Change Description
% =========================================================================
% 21/08/25 CrazyBingo 1.0 Original
% -------------------------------------------------------------------------
% | Oooo |
% +-----------------------------oooO--( )-------------------------------+
% ( ) ) /
% \ ( (_/
% \_)
% -----------------------------------------------------------------------
clear all;
close all;
clc;
% -------------------------------------------------------------------------
% Read PC image to Matlab
IMG1 = imread('../images/scart.jpg'); % 读取jpg图像
IMG1 = rgb2gray(IMG1);
% IMG1 = imread('../images/gsls_test1.tif'); % 读取jpg图像
h = size(IMG1,1); % 读取图像高度
w = size(IMG1,2); % 读取图像宽度
subplot(221);imshow(IMG1);title('原图');
% -------------------------------------------------------------------------
IMG2 = zeros(h,w);
for i = 1:h
for j = 1:w
IMG2(i,j) = (255/255.^2.2)*double(IMG1(i,j)).^2.2;
end
end
IMG2 = uint8(IMG2);
subplot(222);imshow(IMG2);title('Gamma=2.2映射');
% -------------------------------------------------------------------------
IMG3 = zeros(h,w);
for i = 1:h
for j = 1:w
IMG3(i,j) = (255/255.^(1/2.2))*double(IMG1(i,j)).^(1/2.2);
end
end
IMG3 = uint8(IMG3);
subplot(223);imshow(IMG3);title('Gamma=1/2.2映射效果');
% -------------------------------------------------------------------------
THRESHOLD = 127;
E=4;
IMG4 = zeros(h,w);
for i = 1:h
for j = 1:w
IMG4(i,j) = (1./(1 + (THRESHOLD./double(IMG1(i,j))).^E)) * 255;
end
end
IMG4 = uint8(IMG4);
subplot(224);imshow(IMG4);title('对比度增强效果');
% ----------------------------------------------
fid = fopen('..\..\SIM\4_Gamma_Mapping_sim\source_files\image_gray.txt','wt');
for row = 1 : h
for col = 1 : w
fprintf(fid,'%s ',lower(dec2hex(IMG1(row,col),2)));
end
fprintf(fid,'\n');
end
fclose(fid);
fid = fopen('image_gray_gamma.txt','wt');
for row = 1 : h
for col = 1 : w
fprintf(fid,'%s ',lower(dec2hex(IMG2(row,col),2)));
end
fprintf(fid,'\n');
end
fclose(fid);
?
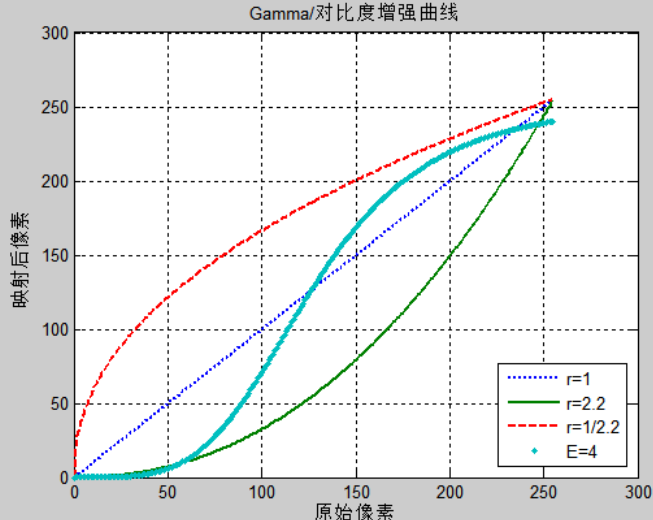
从上图可知,仅个人视觉效果评判,图【2】的效果更好,虽整体相对图【1】偏暗,比如松鼠鼻子看不清了,但细节更清晰;图【3】严重过曝,效果不佳;图【4】稍微过曝,明暗对比度提升。
为了更好的对比图像映射的过程,绘制了Gamma=2.2;Gamma=1/2.2,以及指数对比度的曲线。可见对比度曲线结合了Gamma=2.2及1/2.2的曲线,同时拉伸了亮部和暗部;而Gamma=2.2或者1/2.2仅拉伸了暗部或者亮度。
当然这个过程没有对与错。
?
?
- Gamma映射FPGA实现
- Gamma映射LUT的生成
沿用对比度增强Verilog生成的Matlab代码,如下所示:
% -----------------------------------------------------------------------
clear all;
close all;
clc;
% ----------------------------------------------------------------------
fp_gray = fopen('.\Curve_Gamma_2P2.v','w');
fprintf(fp_gray,'//Curve of Gamma = 2.2\n');
fprintf(fp_gray,'module Curve_Gamma_2P2\n');
fprintf(fp_gray,'(\n');
fprintf(fp_gray,' input\t\t[7:0]\tPre_Data,\n');
fprintf(fp_gray,' output\treg\t[7:0]\tPost_Data\n');
fprintf(fp_gray,');\n\n');
fprintf(fp_gray,'always@(*)\n');
fprintf(fp_gray,'begin\n');
fprintf(fp_gray,'\tcase(Pre_Data)\n');
Gray_ARRAY = zeros(1,256);
for i = 1 : 256
Gray_ARRAY(1,i) = (255/255.^2.2)*(i-1).^2.2;
Gray_ARRAY(1,i) = uint8(Gray_ARRAY(1,i));
fprintf(fp_gray,'\t8''h%s : Post_Data = 8''h%s; \n',dec2hex(i-1,2), dec2hex(Gray_ARRAY(1,i),2));
end
fprintf(fp_gray,'\tendcase\n');
fprintf(fp_gray,'end\n');
fprintf(fp_gray,'\nendmodule\n');
fclose(fp_gray);
% -----------------------------------------------------------------------
% 打印变形后的映射数组Gray_ARRAY
reshape(Gray_ARRAY,16,16)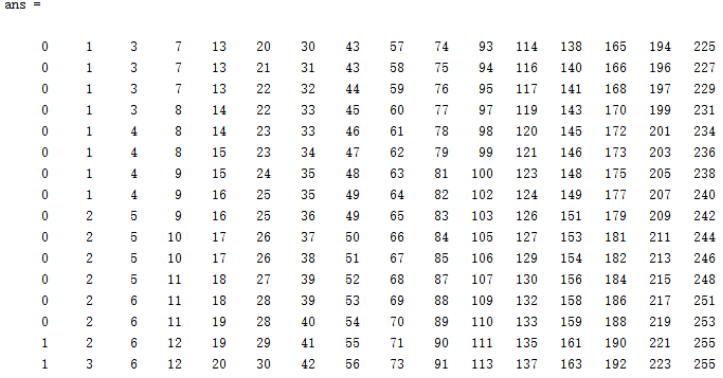
?
由Matlab生成的Verilog代码,如下所示:
?
?
- RTL仿真结果及实测
未完待续,等书出来吧
I am CrazyBingo!
本文为《基于Matlab与FPGA的图像处理教程》中的章节,在正式出版前,我将率先在公众号/博客中给大家分享出来,请大胆指正!!!


?
?