聚类分析原理简介:
聚类分析是对样品或变量进行分类的一种多元统计方法,目的在于将相似的实物归类。
聚类分析并不是一种纯粹的统计技术,在方法基础上与分布理论和显著性无关,一般不用于从样本推断总体的研究。在市场研究中,聚类分析主要用于市场细分、研究消费者行为,寻找新的潜在市场和左尾其他统计分析的预处理等。
聚类分析的基本概念
聚类(clustering)是将某个对象集划分为若干组(class或cluster)的过程,使得同一个组内的数据对象是具有较高的相似度,而不同的组中间的数据对象是不相似的,相似或者不相似的定义基于属性变量的取值确定,一般采用个对象间的距离(欧几里得距离)来表示。
聚类分析属于无监督的学习方法,它不依赖事先已知的数据分类,也不依赖标有数据类别的训练样本集合。正因为如此,聚类分析是一种通过观察的学习方法,而不是通过示例取学习规则。
思想:
聚类算法就是用K_Means聚类实现的,用欧几里得距离为依据判别点之间的相似性。
-
如果二维平面上的一堆点要分成三类,那么首先会随机选择三个点,然后平面中所有的点都会和这三个选择的中心点求距离,离哪个点近,就划分到哪个中心点类别中,初步的标记好三个分类。
-
然后这三个分类再对每个分类求其质心,得出三个中心点。这个求质心的过程,是找出一个点,使得这个点到所有的点的距离最小化。因为存在无数个点使得距离最大,单总有一个点,会得到最小的距离。求出中心点后,在重新计算所有点到这三个中心点的距离,重新划分类别。
-
以此重复循环,最终得到划分后的类别与求得中心点后计算得到的类别没有差别,或者是距离在一定的误差范围类,即结束分类器。
用spss进行快速聚类,K_均值聚类。表格如下,删除了几个用不到的信息。
我们对以上表格按照salary薪资,和salbegin起始工资,划分类别。
先看一下他们的散点图分布:
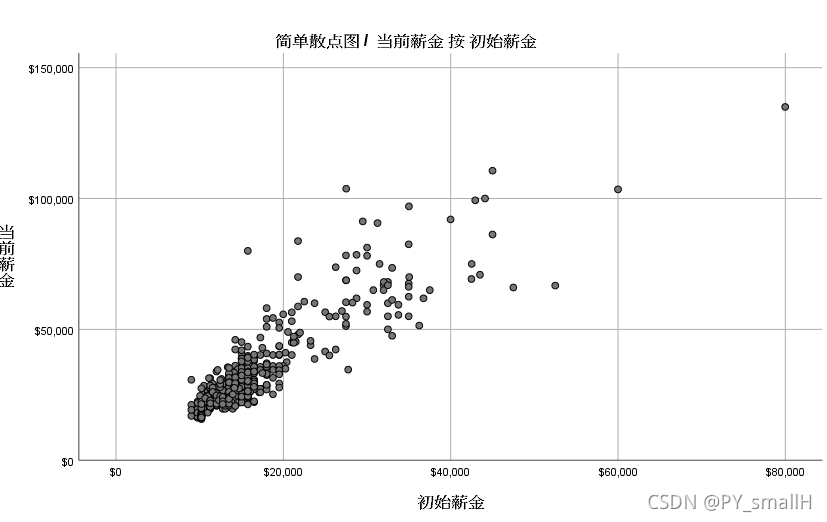
我们把这些点分成三个类别。
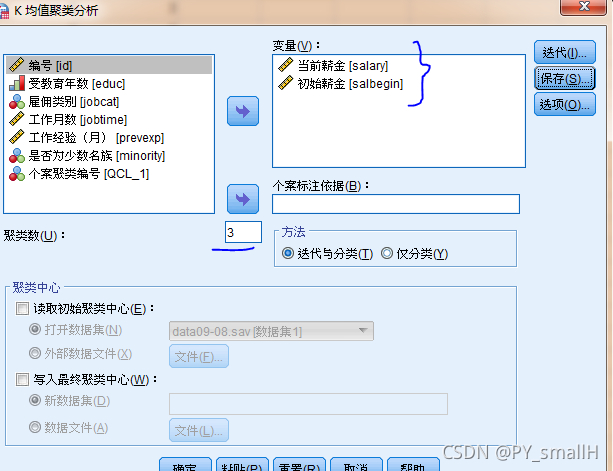
选择保存按钮点击保存分类后的类别。
最终结果会在spss表格中保存分类的结果类别。
spss分析输出:
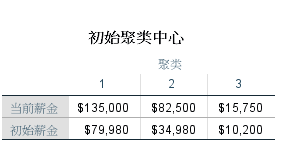
初始的聚类中心选择的三个点。
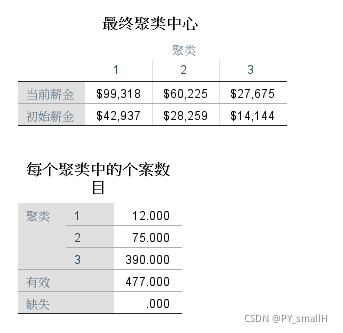
最终的聚类中心点,和每个类别中的数量。一类别工资高的有12个,中等工资的75人,一般工资占比最多。
最终我们绘图看一下分类的结果:
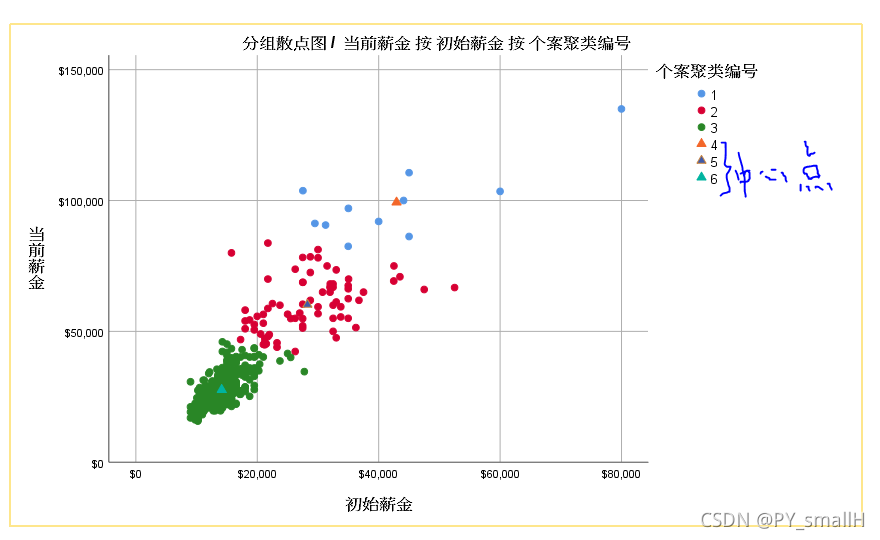
三角形标注的4,5,6三个点是中心点的位置。
然后我又做了另外一件事,用Python中的K_Means方法给这组数据进行分类
km2 = KMeans(n_clusters=3)
km2.fit(df1[["salary","salbegin"]])
plt.figure(figsize=(12,9))
plt.scatter(df1["salbegin"],df1["salary"],c=km2.labels_)
plt.scatter(km2.cluster_centers_[:,1],km2.cluster_centers_[:,0],c='r')
plt.grid(True)
plt.show()
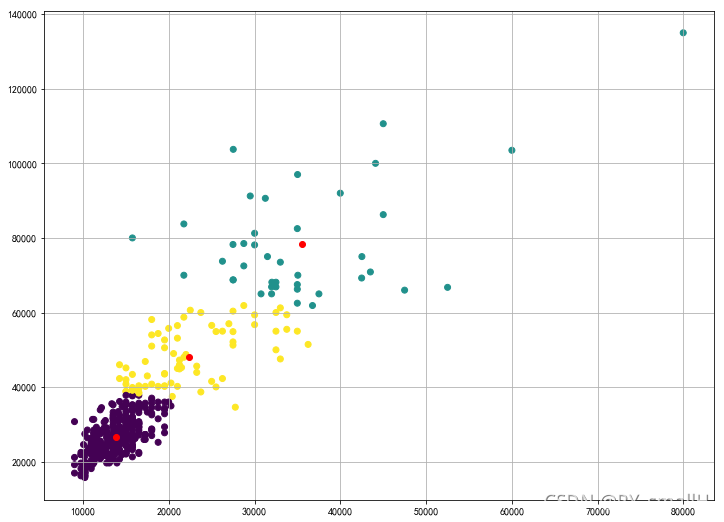
最终得到的三个中心点也不一样。
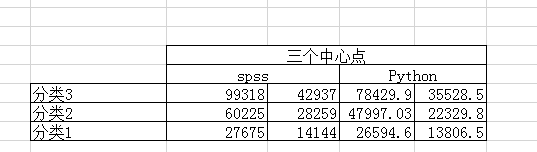
Python中分得每个类别比较均匀,我执行了很多次,虽然每一次在边缘处有一两个点会摇摆,但基本差别不会太大。而且Python中选择的初始化中心点的方法是K_means++,初始化优化算法。
但是spss中的具体方法我没有查到,希望补充。