文章目录
一、BP神经网络简介及算法实现
1.向前传播阶段
1)隐藏层神经元输入
本实验以单隐藏层的神经网络为例,隐藏层神经元的输入为 n e t i = x 1 w 1 i + x 2 w 2 i + ? + x n w n i net_i=x_1 w_{1i}+x_2 w_{2i}+?+x_n w_{ni} neti?=x1?w1i?+x2?w2i?+?+xn?wni?其中n对应输入数据的特征数,为加快收敛速度,本实验中给每一个神经元增加一个偏移量来加快收敛速度。涉及到的代码如下:
def hidden_in(feature, w0, b0):
m = np.shape(feature)[0]
hidden_in = feature * w0
for i in range(m):
hidden_in[i, ] += b0
return hidden_in
2)隐藏层神经元输出
隐藏层神经元的输入经过激活函数f即可得到神经元的输出o=f(net),常见激活函数包括sigmoid、ReLU、Leaky_ReLU和tanh等,其表达式如下,相关代码位于activation.py中。
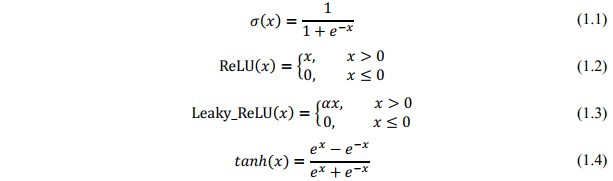
3)输出层神经元
在向前传播阶段,输出层神经元的输入和输出与隐藏层同理,不再重复。
2.向后传播阶段
1)输出层权的调整

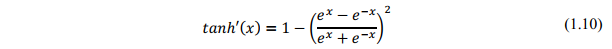
代码示意如下:
delta_output = -np.multiply((label - output_out), act_derivate(output_in, mode=activate))
w1 = w1 - alpha * (hidden_output.T * delta_output)
2)隐藏层权的调整

代码示意如下:
delta_hidden = np.multiply((delta_output * w1.T), act_derivate(hidden_input, mode=activate))
w0 = w0 - alpha * (feature.T * delta_hidden)
3.误差测度(cost function)
向后传播算法的目的是希望缩小实际计算输出的O与理想输出(标签)Y的差距,所以整个过程需要按极小化误差的方式调整权矩阵。网络关于第p个样本的误差测度 E p = 1 2 ∑ j = 1 m ( y p j ? o p j ) 2 E_p=\frac{1}{2}∑_{j=1}^{m}(y_{pj}-o_{pj} )^2 Ep?=21?j=1∑m?(ypj??opj?)2由此可得网络关于整个样本集的误差测度为: E = ∑ p E p E=∑_pE_p E=p∑?Ep?
二、随机生成数据集
为了便于分析不同输入向量维度、分类类别数对于BP算法应用于分类问题的影响,本实验选择借助sklearn库中的make_classification函数随机生成数据并按照8:2的比例划分训练集和测试集写入相应的txt文档中。
关键代码如下:
X1, Y1 = make_classification(n_samples=num, n_features=nfeatute, n_redundant=0, n_clusters_per_class=1, n_classes=nclass)
当特征数目为2或3时,可将数据可视化,图1、2为示例:


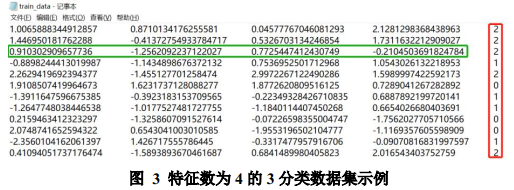
当特征数大于3时,同样地将数据写入txt文档,图3为特征数为4的3分类数据集示例。
※初始化说明
由于本实验使用两级BP神经网络,所以共包含两个权重矩阵W0(输入-隐藏层)和W1(隐藏层-输出),借助random.rand随机对W0、W1及相应的偏置进行初始化。具体代码如下所示:
w0 = np.mat(np.random.rand(n, n_hidden))
w0 = w0 * (8.0 * sqrt(6) / sqrt(n + n_hidden)) - \
np.mat(np.ones((n, n_hidden))) * (4.0 * sqrt(6) / sqrt(n + n_hidden))
b0 = np.mat(np.random.rand(1, n_hidden))
b0 = b0 * (8.0 * sqrt(6) / sqrt(n + n_hidden)) - \
np.mat(np.ones((1, n_hidden))) * (4.0 * sqrt(6) / sqrt(n + n_hidden))
w1 = np.mat(np.random.rand(n_hidden, n_output))
w1 = w1 * (8.0 * sqrt(6) / sqrt(n_hidden + n_output)) - \
np.mat(np.ones((n_hidden, n_output))) * \
(4.0 * sqrt(6) / sqrt(n_hidden + n_output))
b1 = np.mat(np.random.rand(1, n_output))
b1 = b1 * (8.0 * sqrt(6) / sqrt(n_hidden + n_output)) - \
np.mat(np.ones((1, n_output))) * (4.0 * sqrt(6) / sqrt(n_hidden + n_output))
- 可根据情况设置多组对照实验,例如1)不同输入向量(特征)/输出向量(类别)维度的对比实验;2)不同隐藏层神经元个数的对比实验;不同激活函数的对比实验;不同学习率的对比实验等。