【机器学习】特征选择方法
什么是特征选择?
Feature Selection 是在模型构建过程中选择最相关、最有利于提高预测效果的特征子集的过程,也是数据预处理的重要步骤之一。
和降维的区别:
机器学习中的特征选择(Feature Selection)也被称为 Variable Selection 或 Attribute Selection。
虽然特征选择和降维(dimensionality reduction)都是为了减少特征的数量,但是特征选择不同于降维:
降维是创造特征的新组合,比如PCA 和 SVD。
特征选择则只是从原有特征中进行选择或排除,不涉及原有特征的转变。
为什么需要特征选择?
训练机器学习模型之前的特征选择是很重要的预处理过程,之所以进行特征选择有以下几点很重要的原因:
- 现实任务中经常遇到维数灾难问题,如果能选择出重要特征,再进行后续学习过程,则维数灾难可以大为减轻。
- 去除不相关的特征往往会降低学习任务的难度,使模型更易理解(比如,使决策树的规则变得更加清晰)。
- 去除不相关的变量还可以尽量减少过拟合的风险,尤其是在使用人工神经网络或者回归分析等方法时,额外的输入变量会增加模型本身的额外自由度,这些额外的自由度对于模型记住某些细节信息会有所帮助,但对于创建一个稳定性良好、泛化性能强的模型却没有好处,也就是说增加额外的不相关变量会增大过拟合的风险(决策树技术是不存在过拟合风险的一个例子,因为标准的决策树一次只选取一个变量)。
特征选择的两个关键环节
想要从初始的特征集合中选取一个包含所有重要信息的特征子集,若没有任何先验知识,则只能遍历所有可能的子集,然而这样在计算上显然不可能,尤其是在特征个数很多的情况下。
可行的方法是:产生一个候选子集,评价它的好坏,基于评价结果产生下一个候选子集,再对其进行评价……持续这一过程,直到找不到更好的子集为止。
这一过程涉及到两个关键环节:如何根据评价结果获取下一个特征子集?如何评价候选特征子集的好坏?
环节一:子集搜索问题
前向搜索:第一个环节是“子集搜索”问题,给定特征集合 a1,a2,…,an,首先选择一个最优的单特征子集(比如 a2)作为第一轮选定集,然后在此基础上加入一个特征,构建包含两个特征的候选子集,选择最优的双特征子集作为第二轮选定子集,依次类推,直到找不到更优的特征子集才停止,这样逐渐增加相关特征的策略成为前向(forward)搜索
后向搜索:类似的,如果从完整的特征集合开始,每次尝试去掉一个无关特征,这样逐渐减少特征的策略称为后向(backward)搜索
双向搜索:前向后向搜索结合起来,每一轮逐渐增加选定相关特征(这些特征在后续轮中确定不会被去除),同时减少无关特征,这样的策略被称为双向(bidirectional)搜索。
上述策略都是贪心策略,仅考虑本轮选定集最优,但若不进行穷举,这样的问题就无法避免。
环节二:子集评价问题
确定了搜索策略,接下来就需要对特征子集进行评价,以离散型属性的信息增益为例:
给定数据集 D,设D 中第 i类样本的比例为 pi(i=1,2,…,n),则信息熵的定义为:
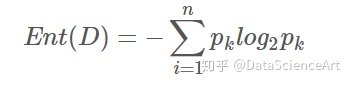
对于属性子集 A,假定根据其取值将 D 成了 V个子集 D1,D2,…,DV,每个子集的样本在 AA上取值相同,于是我们可以计算属性子集 AA的信息增益为:
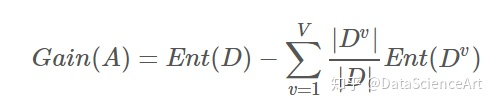
信息增益越大,意味着特征子集 A包含的有助于分类的信息越多。于是,对于每个特征子集,我们可以基于训练集 DD来计算其信息增益,以此作为评价标准。
主要的 特征/特征子集 评价方法(Selection) 如下:
特征子集搜索机制和子集评价机制相结合,就可以得到特征选择方法。例如,将前向搜索和信息熵相结合就和决策树算法非常相似(不同之处是从第二步开始,决策树是在每个孩子节点的数据集上评价特征,而前向搜索依然是在整个数据集上评价特征)。事实上决策树本身就是一种特征选择的方法,树节点的划分属性组成的集合就是选择出的特征子集!
常见的特征选择方法
常用的特征选择方法大致可以分为三类:过滤式(filter)、包裹式(wrapper)和嵌入式(embedding)。
(一)Filter Method
过滤式方法先对数据集进行特征选择,然后再训练模型,特征选择过程与后续模型训练无关。
Relief(Relevant Features)是一种著名的过滤式特征选择方法,该方法设计了一个“相关统计量”来度量特征的重要性。该统计量是一个向量,其每个分量分别对应于一个初始特征,而特征子集的重要性则是由子集中每个特征所对应的相关统计量分量之和来决定。对每个实例x,在x的同类样本中寻找最近邻,称为“猜中近邻”(near-hit)。在x的异类样本中寻找其最近邻,称为“猜错近邻”(near-miss),相关统计量对应于属性j的分量为:
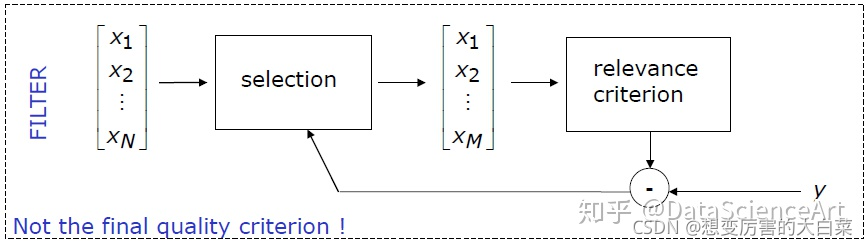
Filter 方法常用的特征子集评价标准包括:相关系数、互信息、信息增益等
更多方法参见 mlr 包支持的所有 Filter 方法。
(二)Wrapper Method
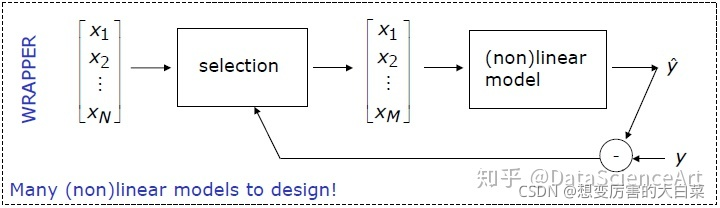
与过滤式特征选择不考虑后续学习器不同,包裹式特征选择直接把最终将要使用的模型的性能作为特征子集的评价标准,也就是说,包裹式特征选择的目的就是为给定的模型选择最有利于其性能的特征子集。
从最终模型的性能来看,包裹式特征选择比过滤式特征选择更好,但需要多次训练模型,因此计算开销较大。
LVM(Las Vegas Wrapper)是一个典型的包裹式特征选择方法。它在拉斯维加斯方法框架下使用随机策略来进行子集搜索,并以最终分类器的误差为特征子集评价标准。LVW的计算开销很大,需要设置停止条件控制参数。
(三)Embedding Method
在前两种特征选择方法中,特征选择过程和模型训练过程是有明显分别的两个过程。
嵌入式特征选择是将特征选择过程与学习器训练过程融为一体,两者在同一个优化过程中完成,即在学习器训练过程中自动地进行了特征选择。嵌入式选择的实例是 LASSO 和 Ridge Regression。
以最简单的线性回归模型为例,其以平方误差为损失函数,则优化目标为:
在样本数较少,样本特征很多的时候,容易陷入过拟合,因此可引入正则化来防止过拟合,
若使用L2范数正则化,则此时优化目标的公式即为岭回归(ridge regression),
若是L1范数正则化,则是LASSO回归(Least Absolute Shrinkage and Selection Operator)。
L1范数和L2范数正则化都有助于降低过拟合风险,但前者还会带来一个额外的好处,它比后者更易于获得“稀疏”(sparse)解,即它求得的w会有更少的非零分类。换言之,采用L1范数比L2范数更易于得到稀疏解。
注意到w取得稀疏解意味着初始的d个特征中仅有对应着w的非零分量的特征才会出现在最终模型中,于是,求解L1范数正则化的结果是得到了仅采用一部分初始特征的模型;所以,基于L1正则化的学习方法就是一种嵌入式特征选择方法,其特征选择过程与学习器训练过程融为一体,同时完成。
此外,L1正则化问题的求解可使用近端梯度下降(Proximal Gradient Descent,PGD),即在每一步对f(x)进行梯度下降迭代的同时考虑L1范数最小化。通过PGD能使LASSO和其它基于L1范数最小化的方法得以快速求解。
由于决策树算法在构建树的同时也可以看作进行了特征选择,因此嵌入式方法可以追溯到 ID3 算法。