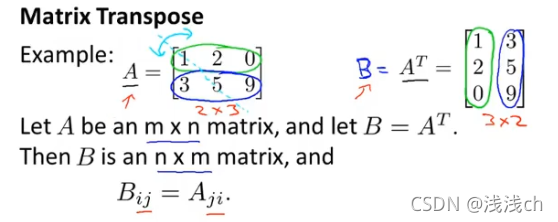（一）矩阵的逆和转置
1、只有方阵(n*n维度)才有逆矩阵，定义如下：
没有逆矩阵的矩阵通常被叫做"singular"（奇异矩阵）或"degenerate"（退化矩阵）。
2、A12=B21，A矩阵的行变成B矩阵的列，A矩阵的列变成B矩阵的行。即为矩阵的转置。
（二）多元线性回归
1、以之前的房屋价格预测问题为例，我们不仅知道房屋大小，还知道卧室数量、楼层数量、房屋年龄等变量，同样预测房屋价格。这时的表示方式如下：
n表示特征量的数目，即变量个数：n=4；
m表示训练样本数：m=47；
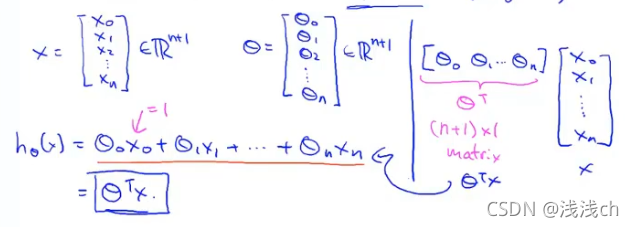
x(i)表示第i条训练样本数据，即一个n维向量；
x(i)j表示第i条训练样本中的第j个特征值。
2、那么这时我们的线性回归假设函数就应表示为：
通常我们增加一个x0=1。
那么我们可以分别写成n+1维的特征向量X、参数向量C塔，并重新展开假设函数，可以看出它的结果就等于两个向量相乘：
（三）多元梯度下降
1、归纳整理上式的假设函数、代价函数、梯度下降过程的式子如下：（这里建议直接表达成C塔向量）
2、接下来我们推导梯度更新式子中的偏导部分：
左边是我们之前的两个特征量时的情况，可以看作是右边式子的特殊情况（因为其实左边C塔0、C塔1的推导与右边C塔0、C塔1的式子相同）；右边式子是我们现在讲的多元(多个特征量)时的情况。
（四）梯度下降之特征缩放
1、在梯度下降过程中要确保不同特征的取值在相近的范围内，用房屋价格预测问题（假设只已知房屋大小、卧室数量两个变量）来解释就是：
房屋大小在0-2000平方米范围内，卧室数量在1-5个，那么画出来的代价函数的等值线将是又高又椭的椭圆（由于2000与5的比例过于悬殊），那么寻找下山路径（梯度下降）过程将是一条来回震荡的曲线，收敛过程将会很慢很慢。
那么现在用特征缩放的办法执行梯度下降分别除以2000和5，使得x1和x2都在[0,1]的范围，那么得到的代价函数等值线比较圆，收敛速度也更快。
一般来说，我们习惯将xi缩小到[-1,1]的范围。但并不是绝对的，只要与之相近就可以了，比如[0,3]、[-2,0.5]在我们看来都是可以接受的。
事实上，只要我们将不同特征值都缩小到相近范围，我们就认为梯度下降是可行的。
2、均值归一化
更为常见的特征缩放方法是均值归一化。
即我们用xi减一个数来替代xi，使得我的特征值具有为0的平均值，但我们不需要将这一步应用到x0中（因为x0总是等于1，它不具有0的平均值）。更具体的表达如下：
u1表示训练集中特征x1的平均值，s1则是该特征值的范围（一般可认为就是最大值-最小值，更正式的是看作标准差）
将之应用到上例中房屋价格预测问题，可以将x1、x2都缩小到大概[-0.5,0.5]的范围，加快收敛。
（五）梯度下降之选择学习率
1、判断收敛的方法一般有两种：
一种是观察曲线(横轴是迭代次数，纵轴是J(C塔)的最小值)，J(C塔)在每次迭代完成后都应该减小，如果不再减小几乎保持不变了，就认为它收敛；
另一种是自动收敛法，即事先确定一个阈值，当J(C塔)的值小于这个值就认为训练完毕，收敛了。
2、以下这两种曲线都是在学习率阿法值过大的时候造成的。
因为在线性回归函数中，如果选择的学习率足够小的话，梯度值一定会很慢很慢地向最低点移动（定理）。
3、总结来说，学习率阿法如果太小：收敛太慢；如果太大：代价函数可能不减小甚至不收敛。
通常，我们选择学习率，一般按这种顺序尝试：
（六）其他
实际上，我们做回归曲线时不一定就是直线。我们还要根据一定的规律去寻找适配最合适的曲线。
例如：还是房屋价格预测问题，对于这些样本点我们认为非常符合一个二次函数，但是同时考虑到二次函数是一条拱形曲线，也就是说随着房屋大小变大，房屋价格下降，这是不符合常理的。这时候我们可能会想到三次函数，因为三次函数是不断增长的。
但我要提醒你的是，如果这样建立模型，一定要注意特征缩放。因为size的范围为0-1000的话，size的平方范围就是0-1000000等，比例相差很大。