文章目录
前言
主要学习了深度学习中最重要的反向传播的知识点。
一、深度学习简介
深度学习三步骤==1.神经网络 2.模型评估 3.选择最优函数
step1:神经网络
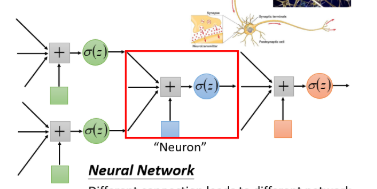
神经网络由神经元组成。(红色方框中就算一个神经元)
神经元(逻辑回归函数)有权重和偏差(即参数)
已知神经元以及其连接方式,就可以将其神经网络看作一个函数function
神经元(未知其参数)连接方式构成了不同的function set
全连接前馈神经网络
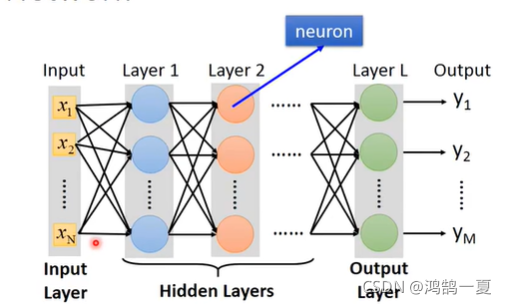
神经网络:1输入层 ;N隐藏层;1输出层
全连接:各层之间两两都连接。
前馈:信号都从前向后传。
矩阵运算
因为深度学习隐藏层非常多,所以如果直接算的话效率是极低的,所以我们后来用GPU做矩阵运算
a
1
=
σ
(
w
1
x
+
b
1
)
{a^1} = \sigma ({w^1}x + {b^1})
a1=σ(w1x+b1)
a
2
=
σ
(
w
2
a
1
+
b
2
)
{a^2} = \sigma ({w^2}{a^1} + {b^2})
a2=σ(w2a1+b2)
以此类推,不断嵌套。
step2:模型评估
用总的损失函数表达:一般用交叉熵(调整参数使其越小越好)
step3:选择最优函数
用前文所讲的梯度下降。以及下文的反向传播。
反向传播
反向传播:有效率的计算梯度向量。重点是:链式法则
链式法则
(1)当
l
y
=
g
(
x
)
z
=
h
(
y
)
\begin{matrix}{l} y = g(x)\\ z = h(y) \end{matrix}
ly=g(x)z=h(y)?时候
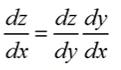
(2)当
x
=
g
(
s
)
x = g(s)
x=g(s) ,
y
=
h
(
s
)
y = h(s)
y=h(s),
z
=
k
(
x
,
y
)
z = k(x,y)
z=k(x,y)时
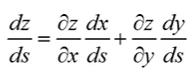
反向传播
?
C
?
w
=
?
+
?
z
?
w
?
C
?
z
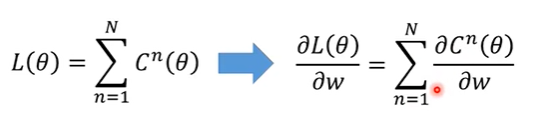
\frac{{\partial C}}{{\partial w}} =?+ \frac{{\partial z}}{{\partial w}}\frac{{\partial C}}{{\partial z}}
?w?C?=?+?w?z??z?C?
1.计算 ? z ? w \frac{{\partial z}}{{\partial w}} ?w?z? Forward Pass
由于
z
=
x
1
w
1
+
x
2
w
2
+
b
z = {x_1}{w_1} + {x_2}{w_2} + b
z=x1?w1?+x2?w2?+b
所以
{
?
z
?
w
1
=
x
1
?
z
?
w
2
=
x
2
\left\{ {\begin{matrix}{} {\frac{{\partial z}}{{\partial {w_1}}} = {x_1}}\\ {\frac{{\partial z}}{{\partial {w_2}}} = {x_2}} \end{matrix}} \right.
{?w1??z?=x1??w2??z?=x2??
已知 input 然后就可以得到output
2.计算 ? C ? z \frac{{\partial C}}{{\partial z}} ?z?C? Backward Pass
已知 z = x 1 w 1 + x 2 w 2 + b z = {x_1}{w_1} + {x_2}{w_2} + b z=x1?w1?+x2?w2?+b, a = σ ( z ) a = \sigma (z) a=σ(z),然后继续迭代得到f 然后作差做到C
?
C
?
z
=
?
a
?
z
?
C
?
a
\frac{{\partial C}}{{\partial z}} = \frac{{\partial a}}{{\partial z}}\frac{{\partial C}}{{\partial a}}
?z?C?=?z?a??a?C?
1.
?
a
?
z
=
σ
(
z
)
\frac{{\partial a}}{{\partial z}} = {\sigma } (z)
?z?a?=σ(z)的导数
2.
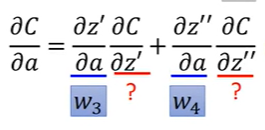
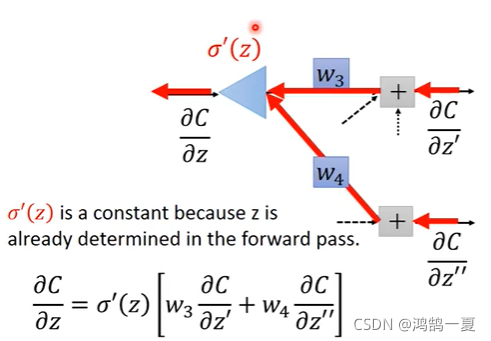
所以我们要做的
从最后一个输出值向前面走,(根据上文的式子),反向传播来计算
?
C
?
z
\frac{{\partial C}}{{\partial z}}
?z?C?。
总结
最主要的是学习到了反向传播,通过公式的推导,让我清楚计算梯度,不单单是只需要反向传播,实际上是反向传播和前向传播的结合。反向传播不需要理解为从前往后一项一项展开,而是从后往前推进,计算量和前向传播一样。