开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 2021高教社杯E题 -> 正文阅读

[人工智能]2021高教社杯E题

参考文献

Kmeans 聚类：https://towardsdatascience.com/k-means-clustering-algorithm-applications-evaluation-methods-and-drawbacks-aa03e644b48a
三次插值法 Python：https://docs.scipy.org/doc/scipy/reference/reference/generated/scipy.interpolate.interp1d.html#scipy.interpolate.interp1d
数值积分 Python：https://docs.scipy.org/doc/scipy-1.4.1/reference/generated/scipy.integrate.trapz.html
PCA 解释方差占比：https://ro-che.info/articles/2017-12-11-pca-explained-variance

本人专挑数据挖掘、机器学习和 NLP 类型的题目做，有兴趣也可以逛逛我的数据挖掘竞赛专栏。

如果本篇博文对您有所帮助，请不要吝啬您的点赞 😊

赛题官网：http://www.mcm.edu.cn/html_cn/node/4d73a36cc88b35bd4883c276afe39d89.html

第一题

第1题旨在根据附件一给出的不同编号的药材的中红外谱数据，研究药材的种类。意思已经很明显了，就是一个聚类的问题。

传统的聚类算法在这个问题中是不适用的原因在于：在中红外谱数据中，每个药材的数据（每一行），以其说可以看成一个点，不如说可以看成一条线，这是一个线的聚类问题，而非点的聚类问题。

因此如果用碘的聚类去解决，就会导致“点”的维度太多，而数据量较少，导致聚类的效果不好。另一方面，附件一中的数据已经帮我们标准化过了，并且每一列的数据的量纲都是相同的，因此我们不能直接套用点的聚类去解决这个问题。

当然我们可以结合点的聚类来进行线的聚类，为了更好的阐述，我们首先简要地介绍一下，点聚类的常见方法： Kmeans 聚类方法

Kmeans 聚类

这里采用的 Kmeans 聚类算法如下：

$\begin{aligned} \text{1、}& \text{选择一个聚类簇数 K} \\ \text{2、}& \text{从数据集中任意地选出个 K 个点，作为聚类中心} \\ \text{~~~~3、}& \text{求出数据集中的每个点与这 K 个聚类簇的距离，并根据与聚类簇距离的远近，将数据划分成 K 个子数据集} \\ \text{~~~~4、}& \text{将 K 个子数据集的均值作为新的聚类中心} \\ \text{~~~~5、}& \text{重复步骤 3、4，直到聚类簇不发生变化为止} \\ \end{aligned}$

距离表示

若采用上述的聚类算法，我们可以看到最关键的一步是如何表示数据集中的每个点与聚类簇的距离：

数据分析

为了更好的分析数据，我们首先将数据进行可视化。当然将所有附件一中的药材的红外谱图画出来是有点不现实的，因此我们挑出编号为0 100 200 300 400的5个药材来展示，其药材的中红外谱图如下所示：
在这里插入图片描述

从上图可以看出药材 200 很明显与其他药材的差距是很大，这是因为药材 200 的吸光度曲线，与其他药材的吸光度曲线的 "距离” 太大了。

积分法表示距离

对于直线来说距离比较好求，但对于曲线来说，距离应该如何定量表示呢？

这里可以考虑采用积分的方法：
$\begin{aligned} \text{距离} = \int_{x=652}^{3999}\Big| y_1 - y_2 \Big| dx \end{aligned}$
式中， $y_1,y_2$ 分别为用于求距离的两种药材的曲线，采用上述公式就可以将曲线与曲线之间的距离量化表示。

鱿鱼我们没有曲线的具体表达式，因此只能用数值积分来求解，但是鉴于 X 轴的数据点间隔比较大，进行积分时产生的误差就会较大。因此在进行积分之前，我们可以采用三次插值法，进行数据填充，从而提高积分的精度。

Kmeans 聚类法对曲线进行聚类

如上所述，我们可以采用 Kmeans 聚类法对曲线进行聚类，同时用上述的积分法求解的距离，作为划分子数据集，从而产生不同的聚类簇，聚类中心由子数据集的所有数据的均值产生。

很多时候，采用 Kmeans 进行聚类，会因为聚类中心的初始化，导致在划分子数据及时，有些聚类中心会没有用到。例如选定的聚类簇数 K，很有可能因为聚类中心的初始化不当，导致仅划分出了 K-1 各个子数据集。另外选择一个较好的初始化聚类中心，也可以提高算法的迭代效率，这里采用的一种初始化聚类中心的方法如下所示：
$\begin{aligned} \text{1、}& \text{选择一个聚类簇数 K} \\ \text{2、}& \text{从数据集} X\in\{x_1,x_2, \cdots, x_n\} \text{中任意地选出个 1 个点，作为第一个聚类中心，记为} c_1 \\ \text{3、}& \text{根据概率} \frac{D(x_i)^2}{\sum_{i=1}^n D(x_i)^2} \text{从} X \text{中选出} c_2, D(x_i) \text{为} x_i \text{与} c \text{的距离}\\ \text{4、}& \text{重复步骤 3 直到聚类中心数为 K} \\ \end{aligned}$
在产生新的聚类中心时，距离公式 $D(x_i)$ 应是 $x_i$ 与目前为止被选中的所有聚类中心 $c={c_1, c_2,\cdots}$ 的距离之和。

Elbow 法选择聚类簇数

采用 Kmeans 方法进行聚类11个比较困难的点在于聚类簇数的选择上，虽然聚类簇数的选择具有一定的主观性，但是我们可以借助一些方法，来帮助我们选择一个较好地聚类簇数 K。

这里我们遍历 $K=\{1,2,\cdots, 21\}$ ，并求出每一个 K 下，数据集与其各自的聚类中心的距离之和，如下图所示：

在这里插入图片描述

根据 Elbow 图的拐点原则，可以选择 K=4,8,12,16 作为聚类簇数。考虑到距离之和越小聚类的效果越好，因此这里选择 K=8 作为最终的聚类簇数。

第一问求解

综上所述，我们选择 K=8 的 Kmeans 聚类法，对附录 1 中的数据进行聚类，最终得出 8 个聚类中心如下所示：

在这里插入图片描述

实际上从上图也可以看出，将聚类簇数设置为 K=2 会好一点，我们在求解 K=2 的情况，得出各聚类中心的中红外谱图如下所示：
在这里插入图片描述

K=8 时，在我们的结果中，子数据集 k=0 也就是聚类簇 0 的数量占了绝大部分，其他聚类簇包含的数据量仅仅为 1~2 个！所以可以认为，附件一中包含的药材种类大致有8种档，其中有一种占了绝大部分，其红外光谱图的特性，如上图的蓝色曲线所示（K=8时），这里就不再多做赘述了。

缺点与改进

该算法的缺点分析

上述聚类得出某一聚类簇包含的数据量及占绝大多数，这实际上可能意味着聚类的效果并不好！笔者亦调整了距离的计算公式，如用：
$\int_{x=652}^{3999} \Big( y_1 - y_2 \Big)^2 dx$
Down得出的聚类的效果都差不多，依旧是某个聚类簇包含的数据量占绝大多数。这可能是以下三个原因造成的：

聚类簇数的选择不够恰当，应该再选多一点；
数据集原本就是这样；
以积分表示距离，实际上忽略了曲线的细节。比如一条曲线的前半部分和另一条曲线的后半部分，与聚类中心对应的部分的差距是相同的，那么这两条曲线可能会被归为一类！（这可能是主要原因）

改进方法

如果真的要改进，应该破而后立，不能再用这种以积分的形式表示距离，从而采用点聚类的方法来聚类曲线。我们可以考虑传统的点聚类方法，然后将每一段波数的数据采用均值等方式合并成一列，从而降低数据量，在采用点距类的方式进行聚类即可。

虽然这样做也会造成一些细节无法体现，但考虑到同一个药材的情况下，波数 $x$ 附近的波数区间 $[x-\delta, x+\delta]$ 的吸光率是非常接近的，因此这些细节忽略了也影响不大，所以可以这么做。

博主这里没有实现这种改进方法，各位聪明的读者可以根据我的代码，自己实现一个。

第二题（第三题、第四题）

说实话，这一题我想了很久，因为像这种比赛的话，一般是第1题要作为第2题的基础的。但我们第一题，采用了曲线聚类的方法，难以分析出各波段的特征。理想的第1题的解法应该是考虑并分析各波段的数学特性，再来进行聚类；或者将数据进行降维，再来进行聚类。于是第2题可以在第1题的基础上进行数据降维，于是问题二并可以作为一个机器学习的经典问题——分类问题来解决。

所以我们在第2题中考虑，先考虑将数据进行降维。在此之前，我们先用上述曲线锯类的方法，对附件2的数据进行一番分析吧。

聚类分析

选择聚类簇数为 K=9，对附件2的数据进行聚类，得到9个聚类中心，如下图所示：

在这里插入图片描述

根据聚类结果来看，依旧是聚类簇 0 占了绝大部分数据。从上图来看，聚类中心 0 比较棱角鲜明，因此我们也可以猜到大部分的药材都是差不多跟聚类中心 0 一样的曲线走向的。

另外从上图也可以看出，聚类的几个聚类中心，它们都比较接近，换句话说，这个药材可能是同一种药材，只是因为他们的场地不同导致他们的吸光率不同罢了。

从上图可以看出我们完全可以将数据，作为用于分类问题的机器学习训练数据和测试数据。

数据降维

我们对数据进行 PCA 降维，为了观察 PCA 降维后的效果，我们可以采用解释方差占比来衡量。所谓解释方差占比可以定量地衡量，数据在降维前后其相似度，或者信息量的保留程度，当解释方差占比为 1 时，可以证明降维前后数据是等效的。

数据再进行 PCA 降维后，若原始数据（高维度）能够以较少的正交数据（低纬度）完全表示，则数据转换前后原始数据的总方差，欲穷转换后的数据的总方差是相等的。

PCA 降维原理是在于：

设原始数据 $X=(x_1, x_2, \cdots, x_n)$ ，转换后的数据为 $X^\prime=(x_1^\prime, x_2^\prime, \cdots, x_n^\prime)$ ，变量 $x_1, x_2, \cdots, x_n$ 的方差为 $v_1, v_2, \cdots, v_n$ 。一般都，原始数据的 $v_i$ 的大小是无序的，其占比有大有小，很少会出现某个 $v_i$ 占了 $\sum v_i$ 的半壁江山的情况。

而 PCA 转换的精髓，就在于转换后 $X^\prime$ 的，每一个变量的方差 $v_1^\prime, v_2^\prime, \cdots, v_n^\prime$ 之和与 $\sum v_i$ 相等，但往往 $v_1^\prime$ 会占 $\sum v_i^\prime$ 的一大半，一般超过 50%，甚至超过 80%（如本例）。

换句话说，经过 PCA 降维后，前 k 个变量的数据的方差占比很高，这意味着这几个变量已经覆盖了原始数据的大部分信息量，因此可以考虑仅保留这 k 个变量，其余删除即可。

我们对数据进行 PCA 降维，保留 $k=\{1, 2, \cdots, 10\}$ 个变量，并观察保留下来的变量的方差之和，占原始数据的方差总和之比：
$explained_variance_ratio_sum = ∑ i = 1 k v i ′ ∑ v i \text{explained\_variance\_ratio\_sum} = \frac{\sum_{i=1}^{k} v_i^\prime}{\sum v_i}$
如下图所示：
在这里插入图片描述

从上图可以看出，我们可以保留 6 个变量就可以了。但考虑到数据量有600多个，还是蛮多的，因此可以考虑保留较多的信息量，于是本文保留了 9 个变量。

机器学习方法解决分类

如上所述，根据附件 2 的数据，识别下述的药材编号的药材产出地：

No	3	14	38	48	58	71	79	86	$\cdots$	618
OP

而附件 2 给出了许多药材对应的中红外谱数据，以及药材对应的产出地。因此这是一个机器学习中的分类问题，我们采用机器学习就可以解决了。

筛选模型参数

鉴于数据量比较充足，我们就不用进行特征过滤了。不过，根据 没有免费午餐定则 ，我们首先要筛选机器学习算法。要筛选算法，必须先选模型参数。为此，我们从如下几个模型中筛选最优模型：

算法	逻辑回归	朴素贝叶斯分类器	k近邻算法	支持向量机	决策树	随机森林	AdaBoost
符号	lr	nb	kNN	SVR	dtr	rf	ada

其中随机森林的基模型是最大深度为 5 的决策树，AdaBoost 的基模型是逻辑回归。

为了筛选参数，首先需要构建一个参数网格，如下所示：

算法	参数网格
lr	无
kNN	{‘n_neighbors’:[3,5,7,9,11,13,15]}
SVR	grid = { ‘C’:[0.01, 0.05, 0.1, 0.3, 0.5, 0.7, 1, 1.5, 1.8, 2, 2.2, 2.5, 3], ‘kernel’:[‘linear’,‘rbf’,‘poly’] }
dtr	grid = {‘max_depth’:[3, 5, 7, 9, 11, 13, 15, 17, 19, 21], ‘ccp_alpha’:[0,0.01,0.05,0.1,0.2,0.3,0.4,0.5]}
rf	基模型个数：5, 10, 15, 20, 25, 30, 35, 40, 45,50, 55, 60, 65, 70, 75, 80, 85, 90
ada	基模型个数：5, 10, 15, 20, 25, 30, 35, 40

（鉴于逻辑回归，朴素贝叶斯分类器不需要进行参数选择，这里并不考虑)

采用 5 折交叉验证、配合网格参数，以 F1 值为目标，最后筛选出各模型的参数如下：

kNN 最佳参数： {‘n_neighbors’: 1}
SVC 的最佳参数: {‘C’: 3, ‘kernel’: ‘linear’}
决策树的最佳参数: {‘ccp_alpha’: 0, ‘max_depth’: 17}
随机森林最佳参数: {‘n_estimators’: 70}
AdaBoost 最佳参数： {‘base_estimator’: LogisticRegression(), ‘n_estimators’: 40}

F1 值（补充介绍）

这里一个需要注意的是采用 F1 值来评价模型或模型参数时，首先是其计算公式：
$F_1 = 2\times\frac{Precision\cdot Recall}{Precision + Recall}$
其中 Precision 为准确率，Recall 为召回率，其计算公式分别如下所示：
$\frac{TP}{TP+FP} ~~~~~ Recall = \frac{TP}{TP+FN}$
其中 TP、FP、TN、FN 为 True、False、Postive、Negative，它们都是对模型的预测结果而言的。比如 TP 意味着模型预测结果是正确的，模型的预测结果为阳性（意思是实际结果也为阳性）。

但细心的读者应该已经注意到了，上述的讨论都是基于阴性阳性这种二分类问题进行的。而我们的题目，很明显是一个多分类问题，OP 一共有 11 个，因此在使用的时候需要对上述的公式进行一定的调整。

多分类问题的评价指标介绍

如前所述要将二分类问题的分类指标用于多分类问题需要进行一定的调整。设多分类问题中 $y$ 共有 N 个取值，即有 N 个类别，那么按照类别将数据集拆分为 N 个子数据集，设模型的预测结果为 $\hat{y}$ ，我们以具体实例解释：设 $y$ 的取值为 {1,2,3}，实际数据集与模型的预测结果如下表所示：

n	$y$	$\hat{y}$
1	1	1
2	1	1
3	1	1
4	1	2
5	2	2
6	2	2
7	2	3
8	3	3
9	3	3

我们根据 $y$ 将数据集拆分为三部分，对于误分类的我们都将其归为 F，正确分类的为 T，于是对于每一个子数据集，可以得到：
$T_{1\sim3} = 3, 2, 2~~~~ F_{1\sim3} = 1, 1,0$
也就是说， $y = 1$ 的大部分数据集，模型分类结果正确的有三个分类，错误的有一个， $y = 2, 3$ 亦然。同样的道理，我们令分类正确为阳性，分类错误为阴性，可以求出 TP、TN、FP、FN：
$TP_{1\sim3} = 3,2,2~~~~~TN_{1\sim3}=0,0,0~~~~ FP_{1\sim3}=0,0,0 ~~~~~ FN+{1\sim3}=1,1,0$
之后，就要求出准确率和召回率，则可以根据上述的 TP, TN, FP, FN 的加权之和来求，权重为对应的子数据集的数量，与数据集的总量之比。

筛选最佳模型

我们采用网格寻优法找到各模型的最佳参数之后，将数据集按 7:3 拆分为训练集和测试集，将模型在训练集中训练并计算相应的 F1 值，从而观察模型的训练效果；再将训练好的模型应用于测试集中，计算模型在测试集中的 F1 值，结果如下所示：

模型 LogisticRegression() 的在训练集和测试集中的 f1_score 分别为：
分别为: 0.5891773875569801, 0.5417854116883021
模型 GaussianNB() 的在训练集和测试集中的 f1_score 分别为：
分别为: 0.6263257700032753, 0.5946591156587332
模型 SVC(C=3, kernel=‘linear’) 的在训练集和测试集中的 f1_score 分别为：
分别为: 0.7187419496172739, 0.6009749514018785
模型 KNeighborsClassifier(n_neighbors=1) 的在训练集和测试集中的 f1_score 分别为：
分别为: 1.0, 0.4318789628445539
模型 DecisionTreeClassifier(ccp_alpha=0, max_depth=17) 的在训练集和测试集中的 f1_score 分别为：
分别为: 1.0, 0.4782662778199531
模型 RandomForestClassifier(max_depth=5, max_features=0.33, max_samples=0.67,
n_estimators=70) 的在训练集和测试集中的 f1_score 分别为：
分别为: 0.8457179907152589, 0.5963864578820567
模型 AdaBoostClassifier(base_estimator=LogisticRegression(), n_estimators=40) 的在训练集和测试集中的 f1_score 分别为：
分别为: 0.41307974611296583, 0.3791410820158239

综合考虑的话，从上面的7个模型来看，很明显 kNN 算法、决策树、随机森林过拟合了；而 AdaBoost、逻辑回归、贝叶斯分类器有些欠拟合，只有 SVC 还勉强可以用。

我们采用精确度准确率和召回率来评价模型，可得：

SVC 模型在训练集中的精确度为： 0.7282608695652174
SVC 模型在训练集中的准确率为： 0.7351819562045411
SVC 模型在训练集中的召回度为： 0.7282608695652174
SVC 模型在测试集中的精确度为： 0.6212121212121212
SVC 模型在测试集中的准确率为： 0.671923571338776
SVC 模型在测试集中的召回度为： 0.6212121212121212

预测结果如下所示：
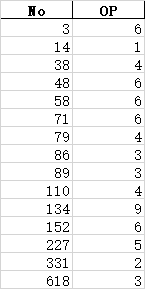
在这里插入图片描述

深度学习：多层感知器模型解决

除了机器学习之外，我们还可以用深度学习的方法来解决这个分类问题，这里采用一种比较简单的深度学习模型——多层感知器来解决附录 2 中的分类问题。

特征预处理

待采用深度学习进行分类问题时，由于附件二中给出的药材种类共有11种，很明显，不是一个双分类问题。直接将次序变量直接用鱼深度学习模型的训练中是无法实现的，因此在训练模型之前，我们需要对数据进行 one-hot 编码法，将次序变量转换为11个二值变量，如下所示：
在这里插入图片描述

模型训练与结果

多层感知器的网络拓扑结构如下所示：

参数	节点个数	激活函数	参数初始化方法	Dropout 正则化率
输入层	9	无	无	无
隐藏层	50	relu	产生于均匀分布	0.2
隐藏层	100	relu	产生于均匀分布	0.2
隐藏层	50	relu	产生于均匀分布	0.2
隐藏层	25	relu	产生于均匀分布	0.2
输出层	11	sigmoid	产生于均匀分布	0

我们以交叉熵为损失函数，以 Adam 为优化算法，用精确度（Accuracy）评价模型，并设置训练步数为 500，梯度下降时用于计算的 batch_size 数量为 100 个数据，训练上述的模型，并计算模型在训练集和测试集中的精确度，得到模型的精确度与训练次数关系图如下所示：
在这里插入图片描述

我们从上图中选择测试集中精确度最大的 epoch 对应的参数，作为模型最终的参数，并求出最佳模型的效果：

模型在训练集中的精确度为: 0.9630434782608696
模型在训练集中的准确率为： 0.9642156224456832
模型在训练集中的召回率为： 0.9630434782608696
模型在训练集中的 f1 值为： 0.9630041142828748
模型在测试集中的精确度为: 0.8131313131313131
模型在测试集中的准确率为： 0.8284411200762084
模型在测试集中的召回率为： 0.8131313131313131
模型在测试集中的 f1 值为： 0.8136931848117631

最终得出的分类结果如下：
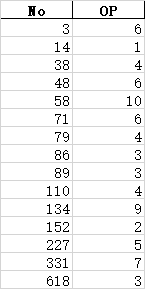
在这里插入图片描述

大家可以自行对比一下机器学习和多层感知器得出的分类结果。

第三题、第四题

其实从第2题中就可以引申到第3题和第4题，因此这里就不实现了，大致的讲一下思路吧。

首先是第3题的中红外数据，这完全可以用第2题来求解。当在求解之前，需要考虑的一个点在于：将数据采用问题一的曲线聚类方法进行聚类，并画出聚类中心，观察各聚类中心的差距大不大，如果各聚类中心的差距并不大，就像第2题一样，那么可以考虑，附件3给出的中红外数据的药材，属于同一类型，只是产出地不同（OP）而已，我们套用第2题的机器学习方法或者深度学习方法就可以解决。

假设聚类出来的，结果各聚类中心曲线的差别比较大，那么意味着附件三中给出的药材不仅是产出地不同，而且还有可能不属于同一种类。此时可以考虑将不同的聚类簇数据单独提取出来，在采用问题2的方法逐个击破，确保用问题二进行深度学习或机器学习分析时，数据集中的药材是属于同一种类的。

对于近红外光谱数据也是一样。

其次是第4题，第4题要求我们根据所给出的数据，对药材的种类和产出地进行分类，这实际上也是一个分类问题，不同的一点在于这是一个多标签分类，它有两个分类标签，也即药材的种类和产出地。这两个标签都是次序变量，因此在进行 one-hot 编码时，无论次序变量有多少个，我们都可以将其转换为多个二值变量进行替代，因此说到底，我们可以用问题 2 中的深度学习方法来解决问题 4。

另一种方法是将药材的种类和产出地拆分出来，然后用问题二中的深度学习方法或机器学习方法单独对待。