FFT
1. FFT原理
原理
-
FFT(Fast Fourier Transformation),中文名快速傅里叶变换,用来加速多项式乘法。
-
朴素高精度乘法时间复杂度是 O ( n 2 ) O(n ^ 2) O(n2),
n是数据位数;但FFT能在 O ( n × l o g ( n ) ) O(n \times log(n)) O(n×log(n))的时间内解决。 -
假设给定一个多项式:
A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . a n ? 1 x n ? 1 A(x) = a_0 + a_1 x + a_2 x^2 + ... a_{n-1} x^{n-1} A(x)=a0?+a1?x+a2?x2+...an?1?xn?1
-
则给定我们任意
n个多项式上的不同点可以唯一确定这个n-1次多项式。这也被称为多项式的点表示法。如下是证明: -
假设多项式上的
n个不同点为 ( x 1 , y 1 ) 、 ( x 2 , y 2 ) 、 . . . 、 ( x n , y n ) (x_1, y_1)、(x_2, y_2)、...、(x_n, y_n) (x1?,y1?)、(x2?,y2?)、...、(xn?,yn?),带入可得:
{ a 0 + a 1 x 1 + a 2 x 1 2 + . . . a n ? 1 x 1 n ? 1 = y 1 a 0 + a 1 x 2 + a 2 x 2 2 + . . . a n ? 1 x 2 n ? 1 = y 2 a 0 + a 1 x 3 + a 2 x 3 2 + . . . a n ? 1 x 3 n ? 1 = y 3 . . . a 0 + a 1 x n + a 2 x n 2 + . . . a n ? 1 x n n ? 1 = y n \begin{cases} a_0 + a_1 x_1 + a_2 x_1^2 + ... a_{n-1} x_1^{n-1} = y_1 \\ a_0 + a_1 x_2 + a_2 x_2^2 + ... a_{n-1} x_2^{n-1} = y_2 \\ a_0 + a_1 x_3 + a_2 x_3^2 + ... a_{n-1} x_3^{n-1} = y_3 \\ ... \\ a_0 + a_1 x_n + a_2 x_n^2 + ... a_{n-1} x_n^{n-1} = y_n \\ \end{cases} ????????????????a0?+a1?x1?+a2?x12?+...an?1?x1n?1?=y1?a0?+a1?x2?+a2?x22?+...an?1?x2n?1?=y2?a0?+a1?x3?+a2?x32?+...an?1?x3n?1?=y3?...a0?+a1?xn?+a2?xn2?+...an?1?xnn?1?=yn??
- 系数矩阵为(这里
a被看成变量):
∣ 1 x 1 x 1 2 . . . x 1 n ? 1 1 x 2 x 2 2 . . . x 2 n ? 1 1 x 3 x 3 2 . . . x 3 n ? 1 . . . 1 x n x n 2 . . . x n n ? 1 ∣ = Π 1 ≤ j < i ≤ n ( x i ? x j ) ( ) \begin{vmatrix} 1 & x_1 & x_1 ^ 2 & ... & x_1 ^ {n-1} \\ 1 & x_2 & x_2 ^ 2 & ... & x_2 ^ {n-1} \\ 1 & x_3 & x_3 ^ 2 & ... & x_3 ^ {n-1} \\ &&... \\ 1 & x_n & x_n ^ 2 & ... & x_n ^ {n-1} \end{vmatrix} \tag{} = \Pi _ {1 \le j < i \le n} (x_i - x_j) ∣∣∣∣∣∣∣∣∣∣?1111?x1?x2?x3?xn??x12?x22?x32?...xn2??............?x1n?1?x2n?1?x3n?1?xnn?1??∣∣∣∣∣∣∣∣∣∣?=Π1≤j<i≤n?(xi??xj?)()
-
因为所有的
x不相同,因此行列式不等于0,所以原方程组存在一组唯一解。 -
我们希望找到原多项式的一个点表示法,并且通过这个点表示法可以推出原多项式的系数。这是后面要着重讨论的内容。下面需要讨论一个问题:为什么需要将多项式变为点表示法?
-
假设给定第二个多项式:
B ( x ) = b 0 + b 1 x + b 2 x 2 + . . . b m ? 1 x m ? 1 B(x) = b_0 + b_1 x + b_2 x^2 + ... b_{m-1} x^{m-1} B(x)=b0?+b1?x+b2?x2+...bm?1?xm?1
-
需要求解多项式 C ( x ) C(x) C(x), C ( x ) = A ( x ) × B ( x ) C(x) = A(x) \times B(x) C(x)=A(x)×B(x)。
-
如果给定我们
n+m-1个点,如下:
( x 1 , A ( x 1 ) ) 、 ( x 2 , A ( x 2 ) ) 、 . . . . . . 、 ( x n + m ? 1 , A ( x n + m ? 1 ) ) ( x 1 , B ( x 1 ) ) 、 ( x 2 , B ( x 2 ) ) 、 . . . . . . 、 ( x n + m ? 1 , B ( x n + m ? 1 ) ) (x_1, A(x_1))、(x_2, A(x_2))、......、(x_{n+m-1}, A(x_{n+m-1})) \\ (x_1, B(x_1))、(x_2, B(x_2))、......、(x_{n+m-1}, B(x_{n+m-1})) (x1?,A(x1?))、(x2?,A(x2?))、......、(xn+m?1?,A(xn+m?1?))(x1?,B(x1?))、(x2?,B(x2?))、......、(xn+m?1?,B(xn+m?1?))
- 则通过对应点相乘,即可得到 C ( x ) C(x) C(x)的点表示法,如下:
( x 1 , C ( x 1 ) ) 、 ( x 2 , C ( x 2 ) ) 、 . . . . . . 、 ( x n + m ? 1 , C ( x n + m ? 1 ) ) = ( x 1 , A ( x 1 ) × B ( x 1 ) ) 、 ( x 2 , A ( x 2 ) × B ( x 2 ) ) 、 . . . . . . 、 ( x n + m ? 1 , A ( x n + m ? 1 ) × B ( x n + m ? 1 ) ) (x_1, C(x_1))、(x_2, C(x_2))、......、(x_{n+m-1}, C(x_{n+m-1})) \\ = (x_1, A(x_1) \times B(x_1))、(x_2, A(x_2) \times B(x_2))、......、(x_{n+m-1}, A(x_{n+m-1}) \times B(x_{n+m-1})) (x1?,C(x1?))、(x2?,C(x2?))、......、(xn+m?1?,C(xn+m?1?))=(x1?,A(x1?)×B(x1?))、(x2?,A(x2?)×B(x2?))、......、(xn+m?1?,A(xn+m?1?)×B(xn+m?1?))
- 上述计算量是
O
(
n
+
m
)
O(n + m)
O(n+m)的,然后将
C的点表示转化为多项式,即可得到两个多项式的乘积。
-
下面讨论如何得到 A ( x ) A(x) A(x) 的点表示法,以及如何根据点表示法得到原多项式。
-
首先说明:这两种转化的时间复杂度都是 O ( n × l o g ( n ) ) O(n \times log(n)) O(n×log(n)) 的。
-
这里需要取
n个点,这n个点的取法是复数域上的单位根。复数域上的单位根:将单位圆分成n份,每一份对应的复数即为选择的点,如下图:
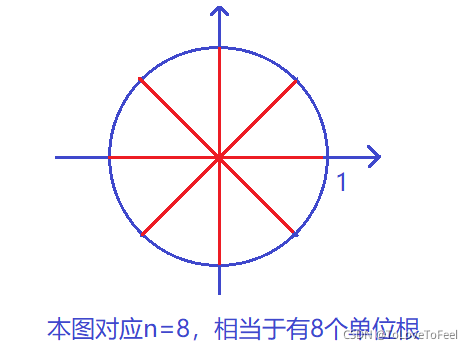
-
使用 ω n k \omega _n^k ωnk? ( 0 ≤ k ≤ n ? 1 0 \le k \le n-1 0≤k≤n?1)表示这
n个单位根。 -
复数加法:和向量加法类似,满足平行四边形法则;复数乘法:几何意义是两复数长度相乘,角度为两复数角度相加。
-
单位根具有的性质:
-
(1) ω n i ≠ ω n j \omega_n^i \neq \omega_n^j ωni??=ωnj?,对于 ? ? i ≠ j \forall \ i \neq j ??i?=j;
-
(2) ω n k = c o s ( 2 k π n ) + i × s i n ( 2 k π n ) \omega_n^k = cos(\frac{2k\pi}{n}) + i \times sin(\frac{2k\pi}{n}) ωnk?=cos(n2kπ?)+i×sin(n2kπ?);
-
(3) ω n 0 = ω n n = 1 \omega_n^0 = \omega_n^n = 1 ωn0?=ωnn?=1;
-
(4) ω 2 n 2 k = ω n k \omega_{2n}^{2k} = \omega_n^k ω2n2k?=ωnk?;
-
(5) ω n k + n 2 = ? ω n k \omega_n^{k+ \frac{n}{2}} = -\omega_n^k ωnk+2n??=?ωnk?;
-
-
现在知道点表示法的横坐标了,需要带入 A ( x ) A(x) A(x) 求出对应的纵坐标的值,直接带入计算的话,求解这
n个点的时间复杂度是 O ( n 2 ) O(n^2) O(n2) 的,因此不可取,需要使用其他方法求解。 -
这里要求
n是2的整数次幂,如果不足的话,后面补零,后面的推导是基于这一点的。 -
首先将 A ( x ) A(x) A(x) 的奇数项和偶数项分开,如下:
A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . a n ? 1 x n ? 1 = ( a 0 + a 2 x 2 + . . . + a n ? 2 x n ? 2 ) + ( a 1 + a 3 x 3 + . . . + a n ? 1 x n ? 1 ) A(x) = a_0 + a_1 x + a_2 x^2 + ... a_{n-1} x^{n-1} \\ = \big(a_0 + a_2 x^2 + ...+ a_{n-2} x^{n-2} \big) + \big(a_1 + a_3 x^3 + ...+ a_{n-1} x^{n-1} \big) A(x)=a0?+a1?x+a2?x2+...an?1?xn?1=(a0?+a2?x2+...+an?2?xn?2)+(a1?+a3?x3+...+an?1?xn?1)
- 令:
A 1 ( x ) = a 0 + a 2 x + a 4 x 2 + . . . + a n ? 2 x n 2 ? 1 A 2 ( x ) = a 1 + a 3 x + a 5 x 2 + . . . + a n ? 1 x n 2 ? 1 A_1(x) = a_0 + a_2 x + a_4 x^2 + ...+ a_{n-2} x^{\frac{n}{2} - 1} \\ A_2(x) = a_1 + a_3 x + a_5 x^2 + ...+ a_{n-1} x^{\frac{n}{2} - 1} A1?(x)=a0?+a2?x+a4?x2+...+an?2?x2n??1A2?(x)=a1?+a3?x+a5?x2+...+an?1?x2n??1
-
则有: A ( x ) = A 1 ( x 2 ) + x A 2 ( x 2 ) A(x) = A_1(x^2) + x A_2(x^2) A(x)=A1?(x2)+xA2?(x2)。
-
我们一共需要求解
n个横坐标 ω n k \omega _n^k ωnk? 对应的纵坐标的值,其中 k ∈ [ 0 , n ? 1 ] k \in [0, n-1] k∈[0,n?1]。 -
将区间分成两部分考虑,分别是: [ 0 , n 2 ? 1 ] 、 [ n 2 , n ? 1 ] [0, \frac{n}{2}-1]、[\frac{n}{2}, n-1] [0,2n??1]、[2n?,n?1]。
-
当 k ∈ [ 0 , n 2 ? 1 ] k \in [0, \frac{n}{2}-1] k∈[0,2n??1],则 k + n 2 ∈ [ n 2 , n ? 1 ] k + \frac{n}{2} \in [\frac{n}{2}, n-1] k+2n?∈[2n?,n?1],则有:
A ( ω n k ) = A 1 ( ω n 2 k ) + ω n k A 2 ( ω n 2 k ) = A 1 ( ω n 2 k ) + ω n k A 2 ( ω n 2 k ) A ( ω n k + n 2 ) = A 1 ( ω n 2 k + n ) + ω n k + n 2 A 2 ( ω n 2 k + n ) = A 1 ( ω n 2 k ) ? ω n k A 2 ( ω n 2 k ) A(\omega_n^k) = A_1(\omega_n^{2k}) + \omega_n^k A_2(\omega_n^{2k}) = A_1(\omega_{\frac{n}{2}}^k) + \omega_n^k A_2(\omega_{\frac{n}{2}}^k) \\\\ A(\omega_n^{k+\frac{n}{2}}) = A_1(\omega_n^{2k+n}) + \omega_n^{k+\frac{n}{2}} A_2(\omega_n^{2k+n}) = A_1(\omega_{\frac{n}{2}}^k) - \omega_n^k A_2(\omega_{\frac{n}{2}}^k) A(ωnk?)=A1?(ωn2k?)+ωnk?A2?(ωn2k?)=A1?(ω2n?k?)+ωnk?A2?(ω2n?k?)A(ωnk+2n??)=A1?(ωn2k+n?)+ωnk+2n??A2?(ωn2k+n?)=A1?(ω2n?k?)?ωnk?A2?(ω2n?k?)
-
注意到 A 1 ( x ) 、 A 2 ( x ) A_1(x)、A_2(x) A1?(x)、A2?(x) 和 A ( x ) A(x) A(x) 的形式是一样的,因此可以使用分治策略同时求出这些纵坐标对应的值。
-
到此为止,我们可以将系数多项式转化为点表示法,时间复杂度是 O ( n × l o g ( n ) ) O(n \times log(n)) O(n×log(n)) 的。
- 下面考虑如何根据点表示法推出原来多项式的系数。
- 首先是结论,假设点表示法中得到的
n个点为 ( ω n k , A ( ω n k ) ) (\omega_n^k, A(\omega_n^k)) (ωnk?,A(ωnk?)),简记为 ( x k , y k ) (x_k, y_k) (xk?,yk?),则原多项式的系数为:
a k = 1 n ∑ i = 0 n ? 1 y i × ( ω n ? k ) i a_k = \frac{1}{n} \sum _{i=0}^{n-1} y_i \times (\omega_n^{-k}) ^ i ak?=n1?i=0∑n?1?yi?×(ωn?k?)i
- 令:
T ( x ) = y 0 + y 1 x + y 2 x 2 + . . . + y n ? 1 x n ? 1 T(x) = y_0 + y_1 x + y_2 x^2 + ... + y_{n-1} x^{n-1} T(x)=y0?+y1?x+y2?x2+...+yn?1?xn?1
-
其中 y i y_i yi? 可以看成常数,我们需要求解 T ( ω n 0 ) 、 T ( ω n ? 1 ) 、 . . . 、 T ( ω n ? ( n ? 1 ) ) T(\omega_n^0)、T(\omega_n^{-1})、...、T(\omega_n^{-(n-1)}) T(ωn0?)、T(ωn?1?)、...、T(ωn?(n?1)?),这个问题和上面根据系数多项式求解点表示法是一样的,因此可以调用同一个函数解决。
-
下面是证明为什么 a k a_k ak? 的表达式是上述形式。
1 n ∑ i = 0 n ? 1 y i × ( ω n ? k ) i = 1 n ∑ i = 0 n ? 1 ( ( ∑ j = 0 n ? 1 a j ( ω n i ) j ) × ( ω n ? k ) i ) = 1 n ∑ i = 0 n ? 1 ( ( ∑ j = 0 n ? 1 a j ( ω n j ) i × ( ω n ? k ) i ) ) = 1 n ∑ i = 0 n ? 1 ( ∑ j = 0 n ? 1 a j ( ω n j ? k ) i ) = 1 n ∑ j = 0 n ? 1 a j ( ∑ i = 0 n ? 1 ( ω n j ? k ) i ) \frac{1}{n} \sum _{i=0}^{n-1} y_i \times (\omega_n^{-k}) ^ i \\\\ = \frac{1}{n} \sum _{i=0}^{n-1} \Big( \big( \sum_{j=0}^{n-1} a_j (\omega_n^i)^j \big) \times (\omega_n^{-k}) ^ i \Big) \\\\ = \frac{1}{n} \sum _{i=0}^{n-1} \Big( \big( \sum_{j=0}^{n-1} a_j (\omega_n^j)^i \times (\omega_n^{-k}) ^ i \big) \Big) \\\\ = \frac{1}{n} \sum _{i=0}^{n-1} \Big( \sum_{j=0}^{n-1} a_j (\omega_n^{j-k})^i \Big) \\\\ = \frac{1}{n} \sum _{j=0}^{n-1} a_j \Big( \sum_{i=0}^{n-1} (\omega_n^{j-k})^i \Big) n1?i=0∑n?1?yi?×(ωn?k?)i=n1?i=0∑n?1?((j=0∑n?1?aj?(ωni?)j)×(ωn?k?)i)=n1?i=0∑n?1?((j=0∑n?1?aj?(ωnj?)i×(ωn?k?)i))=n1?i=0∑n?1?(j=0∑n?1?aj?(ωnj?k?)i)=n1?j=0∑n?1?aj?(i=0∑n?1?(ωnj?k?)i)
- 现在考虑内部的加和,即 ∑ i = 0 n ? 1 ( ω n j ? k ) i \sum_{i=0}^{n-1} (\omega_n^{j-k})^i ∑i=0n?1?(ωnj?k?)i,令 S ( x ) = ∑ i = 0 n ? 1 x i S(x) = \sum_{i=0}^{n-1} x^i S(x)=∑i=0n?1?xi,则我们需要求解的就是 S ( ω n k ) S(\omega _n^{k}) S(ωnk?)的值。
- 当
k!=0时,有:
S ( ω n k ) = 1 + ω n k + ω n 2 k + . . . + ω n ( n ? 1 ) k ( 1 ) ω n k S ( ω n k ) = ω n k + ω n 2 k + . . . + ω n ( n ? 1 ) k + ω n n k = ω n k + ω n 2 k + . . . + ω n ( n ? 1 ) k + 1 ( 2 ) S(\omega_n^{k}) = 1 + \omega_n^{k} + \omega_n^{2k} + ... + \omega_n^{(n-1)k} \quad (1) \\\\ \omega_n^{k} S(\omega_n^{k}) = \omega_n^{k} + \omega_n^{2k} + ... + \omega_n^{(n-1)k} + \omega_n^{nk} \\\\ = \omega_n^{k} + \omega_n^{2k} + ... + \omega_n^{(n-1)k} + 1 \quad (2) S(ωnk?)=1+ωnk?+ωn2k?+...+ωn(n?1)k?(1)ωnk?S(ωnk?)=ωnk?+ωn2k?+...+ωn(n?1)k?+ωnnk?=ωnk?+ωn2k?+...+ωn(n?1)k?+1(2)
- (1)(2)作差可得: ( 1 ? ω n k ) S ( ω n k ) = 0 (1-\omega_n^{k}) S(\omega _n^{k}) = 0 (1?ωnk?)S(ωnk?)=0,因为 ω n k ≠ 1 \omega_n^{k} \neq 1 ωnk??=1,所以 S ( ω n k ) = 0 S(\omega _n^{k}) = 0 S(ωnk?)=0。
- 当
k==0时,则: ω n k = 1 \omega_n^{k} = 1 ωnk?=1,所以 S ( ω n k ) = n S(\omega _n^{k}) = n S(ωnk?)=n。 - 因此,对于上式,只有当
j==k时才不是0,所以有:
1 n ∑ j = 0 n ? 1 a k ( ∑ i = 0 n ? 1 ( ω n j ? k ) i ) = 1 n ∑ j = 0 n ? 1 a k × n = a k \frac{1}{n} \sum _{j=0}^{n-1} a_k \Big( \sum_{i=0}^{n-1} (\omega_n^{j-k})^i \Big) \\\\ = \frac{1}{n} \sum _{j=0}^{n-1} a_k \times n = a_k n1?j=0∑n?1?ak?(i=0∑n?1?(ωnj?k?)i)=n1?j=0∑n?1?ak?×n=ak?
- 证毕!
-
最后还有一个问题,如何分治,一般来说两种方式,一种是递归,另一种是递推。这里采用自底向上的递推方式。(因为实际运行递归效率较慢)。
-
递推的话就需要考虑每个数会被分到哪个组中。如下图所示,我们从最下面的数向上计算。

-
我们如何确定每个数据在最底层的位置?即给我们的顺序是 a 0 、 a 1 、 a 2 、 a 3 、 a 4 、 a 5 、 a 6 、 a 7 a_0、a_1、a_2、a_3、a_4、a_5、a_6、a_7 a0?、a1?、a2?、a3?、a4?、a5?、a6?、a7?,我们需要得到的顺序是 a 0 、 a 4 、 a 2 、 a 6 、 a 1 、 a 5 、 a 3 、 a 7 a_0、a_4、a_2、a_6、a_1、a_5、a_3、a_7 a0?、a4?、a2?、a6?、a1?、a5?、a3?、a7?。
-
如下图,可以发现,在二进制表示中,对应位置是翻转后的结果:

-
这个可以递归证明,第一次分成两部分一定会把最低位是1的所有数据排到后一半,第二次会把次高位是1的排到对应区间的后一半,因此上述结论成立。
-
例如 a 1 a_1 a1?最终会被放置到二进制位置编号为
100的位置,因为001最低位是1,会被放到后一半,因此所在位置的二进制编号最高位是1,后面同理,因此 a 001 a_{001} a001? 会被放到编号为100的位置。 -
那么如何求出最底层的顺序呢?可以使用递推,使用
rev[i]表示第i个位置应该放置a[rev[i]]。对于上述例子,数组rev中的值为0 4 2 6 1 5 3 7。 -
考虑第
i个位置最终的数据,假设i的二进制表示是abcd,则如果不考d,首先将得到abc,即rev[abc],该值等于cba0,因此还需要rev[abc]>>1,然后将i的最低位取出放置到最高位即可,综上所述,递推式如下:rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (3 - 1))。
2. AcWing上的FFT题目
AcWing 3122. 多项式乘法
问题描述
-
问题链接:AcWing 3122. 多项式乘法

分析
- 模板题,直接应用
fft算法即可。
代码
- C++
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
const int N = 300010; // 2^21 = 2,097,152
const double PI = acos(-1);
int n, m;
struct Complex {
double x, y;
Complex operator+ (const Complex &t) const {
return {x + t.x, y + t.y};
}
Complex operator- (const Complex &t) const {
return {x - t.x, y - t.y};
}
Complex operator* (const Complex &t) const {
return {x * t.x - y * t.y, x * t.y + y * t.x};
}
} a[N], b[N];
int bit; // 项数取对数上取整的值
int tot; // tot = 1 << bit, 项数, 不足的为0
int rev[N]; // i的二进制表示翻转为rev[i]
// inv: 1代表多项式->点表示法,2代表点表示法->多项式
void fft(Complex a[], int inv) {
// 首先将每个数据放置到应该在的位置上
for (int i = 0; i < tot; i++)
if (i < rev[i])
swap(a[i], a[rev[i]]);
// 自底向上递推
for (int len = 1; len < tot; len <<= 1) { // 当前合并两段长度为len的区间
// 这里n=2*len, w(n, 1)对应的角度为2*pi/len = pi/len
auto w1 = Complex({cos(PI / len), inv * sin(PI / len)});
for (int i = 0; i < tot; i += len * 2) { // 枚举区间左端点
// 两个区间分别为[i, i + len - 1], [i + len, i + 2 * len - 1]
auto wk = Complex({1, 0});
for (int j = 0; j < len; j++, wk = wk * w1) {
auto x = a[i + j], y = wk * a[i + j + len];
a[i + j] = x + y, a[i + j + len] = x - y;
}
}
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i <= n; i++) scanf("%lf", &a[i].x);
for (int i = 0; i <= m; i++) scanf("%lf", &b[i].x);
while ((1 << bit) < n + m + 1) bit++;
tot = 1 << bit;
// 递推求解rev
for (int i = 0; i < tot; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
// 将a、b转化为对应的点表示法,仍然存储在a、b中
fft(a, 1), fft(b, 1);
// 使用点表示法求解乘积的点表示,存储到a中
for (int i = 0; i < tot; i++) a[i] = a[i] * b[i];
// 将点表示法转化为多项式
fft(a, -1);
// 输出结果
for (int i = 0; i <= n + m; i++)
printf("%d ", (int)(a[i].x / tot + 0.5)); // +0.5防止出现0.99999变为0的情况
return 0;
}
AcWing 3123. 高精度乘法II
问题描述
-
问题链接:AcWing 3123. 高精度乘法II

分析
-
假设 A = a n ? 1 a n ? 2 . . . a 0 A = a_{n-1}a_{n-2}...a_0 A=an?1?an?2?...a0?,则 A A A 还可以表示成 A = a n ? 1 × 1 0 n ? 1 + . . . + a 0 × 1 0 0 A = a_{n-1} \times 10^{n-1} + ... + a_0 \times 10^0 A=an?1?×10n?1+...+a0?×100。
-
设 A ( x ) = a 0 + a 1 x + . . . + a n ? 1 x n ? 1 A(x) = a_0 + a_1 x + ... + a_{n-1} x^{n-1} A(x)=a0?+a1?x+...+an?1?xn?1,则
A(10)就是最初的原始值。 -
我们利用 A ( x ) 、 B ( x ) A(x)、B(x) A(x)、B(x) 求出两者的积 C ( x ) C(x) C(x),然后
C(10)就是答案。
代码
- C++
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 300000;
const double PI = acos(-1);
struct Complex {
double x, y;
Complex operator+ (const Complex &t) const {
return {x + t.x, y + t.y};
}
Complex operator- (const Complex &t) const {
return {x - t.x, y - t.y};
}
Complex operator* (const Complex &t) const {
return {x * t.x - y * t.y, x * t.y + y * t.x};
}
} a[N], b[N];
char s1[N], s2[N]; // 两个需要乘的数
int res[N];
int rev[N], bit, tot;
void fft(Complex a[], int inv) {
for (int i = 0; i < tot; i++)
if (i < rev[i])
swap(a[i], a[rev[i]]);
for (int len = 1; len < tot; len <<= 1) {
auto w1 = Complex({cos(PI / len), inv * sin(PI / len)});
for (int i = 0; i < tot; i += len * 2) {
auto wk = Complex({1, 0});
for (int j = 0; j < len; j++, wk = wk * w1) {
auto x = a[i + j], y = wk * a[i + j + len];
a[i + j] = x + y, a[i + j + len] = x - y;
}
}
}
}
int main() {
scanf("%s%s", s1, s2);
int n = strlen(s1) - 1, m = strlen(s2) - 1;
for (int i = 0; i <= n; i++) a[i].x = s1[n - i] - '0';
for (int i = 0; i <= m; i++) b[i].x = s2[m - i] - '0';
while ((1 << bit) < m + n + 1) bit++;
tot = 1 << bit;
for (int i = 0; i < tot; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
fft(a, 1), fft(b, 1);
for (int i = 0; i < tot; i++) a[i] = a[i] * b[i];
fft(a, -1);
// 求值
int k = 0;
for (int i = 0, t = 0; i < tot || t; i++) {
t += a[i].x / tot + 0.5;
res[k++] = t % 10;
t /= 10;
}
while (k > 1 && !res[k - 1]) k--; // 去掉高位的0
for (int i = k - 1; i >= 0; i--) printf("%d", res[i]);
return 0;
}