参考资料

霍夫变换直线检测原理

直线可以表达成 $y = k x + b$ 的形式，这是用斜率和截距表达出来的。也可以用“点法式”来表示，表示为 $c o s (θ) ? x + s i n (θ) ? y = ρ$ 的形式，推导过程如链接所示，其中 $θ$ 代表法线方向， $ρ$ 代表法线距离。按照这种原理，建立一个二维数组，如下图所示：
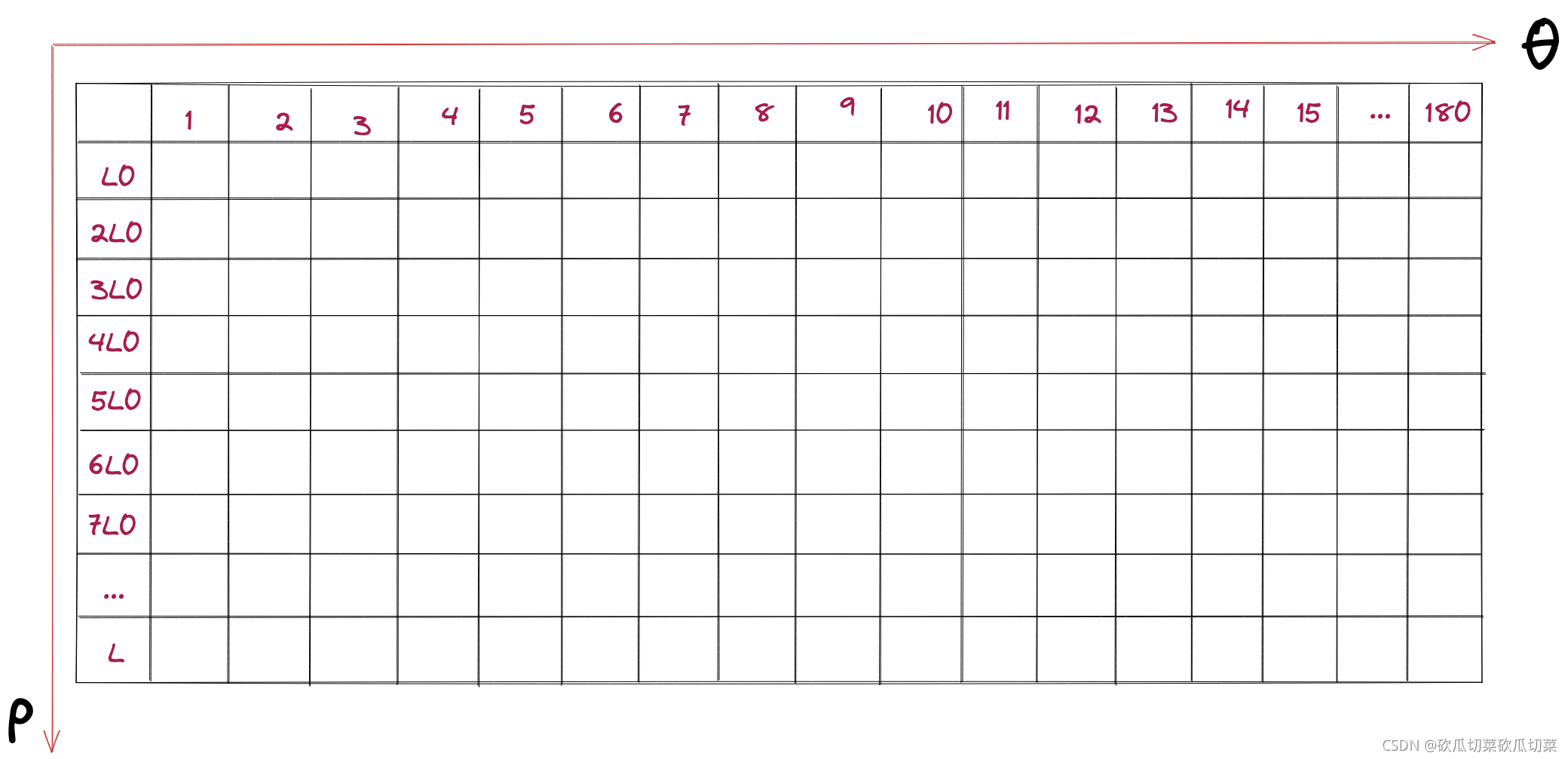
在这里插入图片描述
其中横轴表示角度，角度间隔反映直线检测分辨率，图中是以1°为间隔，那么直线的法线角度只能精确到1°，如果想要增加分辨率，可以设置为其他间隔角度。纵轴表示原点距离直线的法线长度，理论上一张图像中最长的法线长度就是图像的对角线长度，因此我们可以根据距离精度进行分割，如上图所示距离精度为 $L_0$ 。在建立好这个数组后，我们开始进行霍夫直线检测，数组中每个元素就是一个累加器，每个元素均初始化为0。直线检测流程如下图所示：

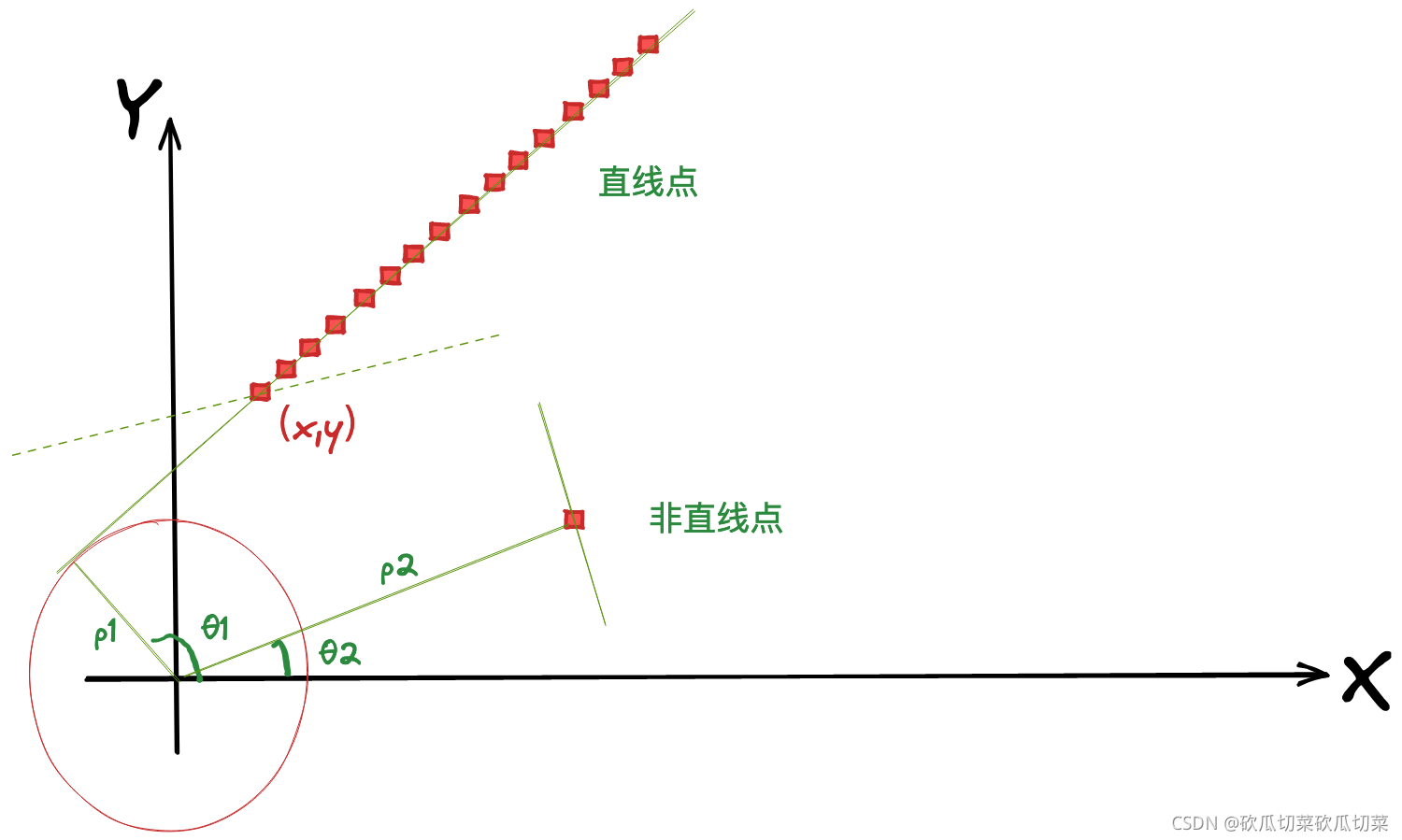
在这里插入图片描述
当图像进行完二值化之后，对每个点进行搜索，如果 $θ$ 的精度为1°，则从0°开始搜索，将 $X 、 Y 、 θ$ 值带入到上述点法式直线方程中，可以算出来一个 $ρ$ 值，并将 $ρ$ 值按照精度等级简化（比如 $ρ$ 算出来值为6.4，如果 $ρ$ 精度为1°，则自动处理为6）。这样，在遍历角度的直线法线角度θ的过程中，我们可以得到180组形如 $(θ, ρ)$ 的数对，将与它们对应点位的元素累加器匹配，并对每个元素进行+1操作。如果这个点在一条直线上，这条直线上第二个点在进行上述操作的时候，必然会在表示这条直线所对应的 $(θ, ρ)$ 位置继续累加，以此类推，则累加器数组中最大元素所对应的 $(θ, ρ)$ 则必然表示一条直线，至此霍夫直线检测完成。如果把每个累加器的数值表达成深浅强度的形式，则效果如下图所示：

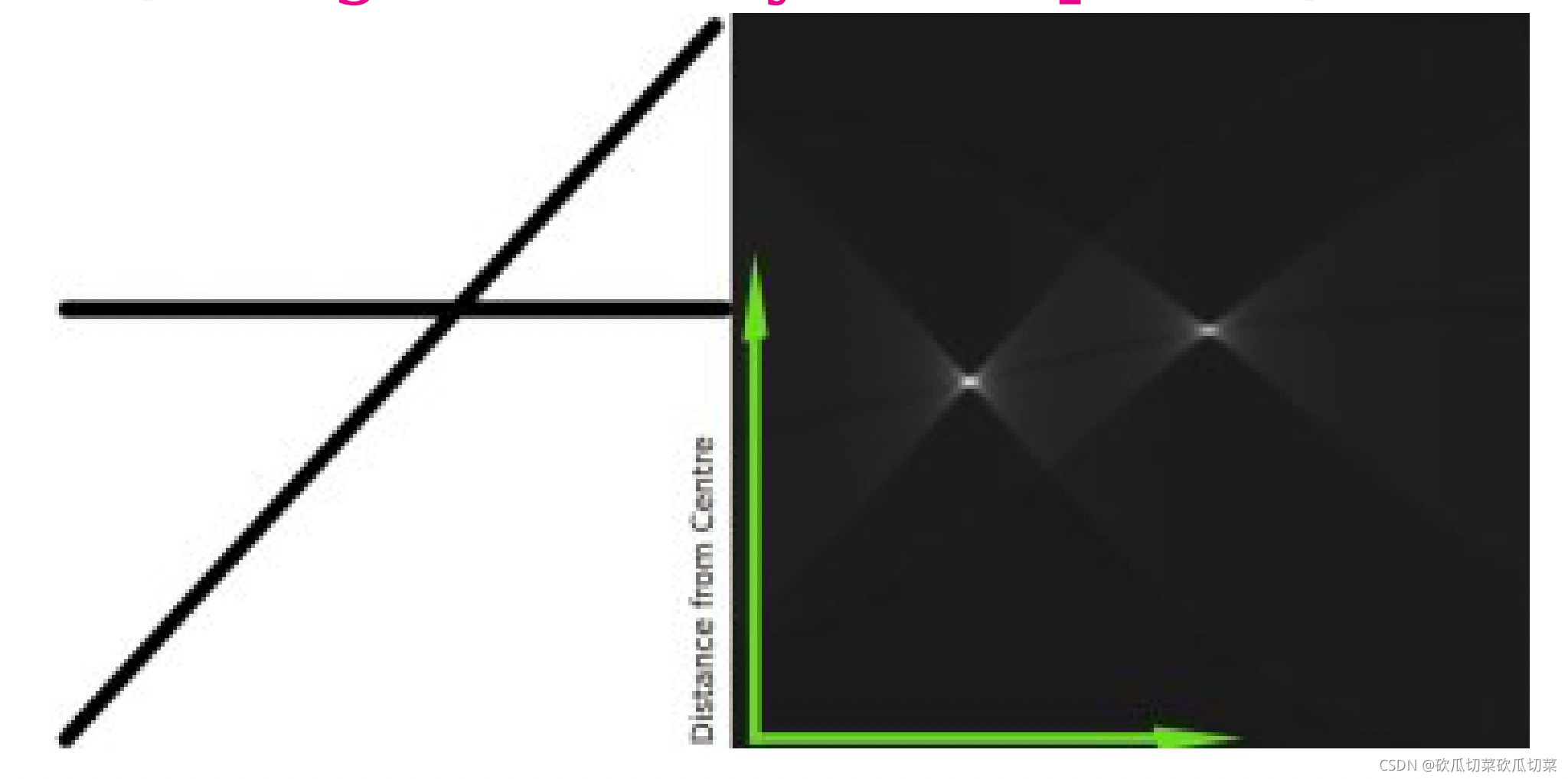
在这里插入图片描述
两个亮点所对应的 $(θ, ρ)$ 则代表直线。

opencv实现霍夫变换

上面介绍的整个过程都被OpenCV封装成了一个函数cv2.HoughLines()返回值就是 $(θ, ρ)$ ， $θ$ 单位是弧度、 $ρ$ 单位是像素，原版详细说明如下图所示：
在这里插入图片描述
函数参数的含义为：

image：待处理的图像，注意一定是二值图像；
lines：直线的输出向量，表达成 $(θ, ρ)$ 的形式（垂直线 $θ$ 为0，水平线 $θ$ 为π/2）；
rho：累加器的距离分辨率，单位是像素；
theta：累加器的角度分辨率，单位是弧度；
threshold：累加器的阈值参数，累加器只有获得足够的累加和（累加器值＞threshold）才会被认为是直线；
srn：对于多尺度霍夫变换，这个参数表示距离分辨率rho的除数。在执行过程中，粗累加分辨率是rho，而更精确的累加分辨率是rho/srn。如果srn和stn均为0，系统采用传统的霍夫变换算法。否则，这两个参数均应该为正数；
stn：对于多尺度霍夫变换，这是角度分辨率theta的一个除数；
min_theta：表示对于标准和多尺度霍夫变换而言检测直线的最小角度，这个数值必须落在0和max_theta之间；
max_theta：表示对于标准和多尺度霍夫变换而言检测直线的最大角度，这个数值必需落在min_theta和max_theta之间；
method：代表下列霍夫变换的变体之一：
- CV_HOUGH_STANDARD：代表经典或标准霍夫变换，每条线用两个浮点数 $ρ, θ$ 表示，其中 $ρ$ 表示原点和这条直线之间的距离， $θ$ 表示代表x轴线和这条直线法线之间的距离。因此，矩阵必须定义为CV_32FC2形式；
- CV_HOUGH_PROBABILISTIC：概率霍夫变换是更有效果一些的（如果图像包括一些长直线段）。将返回直线段而不是整个直线。每段由起点和终点表示，每个矩阵必需为CV_32SC4形式；
- CV_HOUGH_MULTI_SCALE：对经典霍夫变换的多尺度变体。直线编码表达的形式和CV_HOUGH_STANDARD相同。
可选参数1：代表第一个可选独立参数：
- 对于经典霍夫变换，这个参数是没用的（0）；
- 对于概率霍夫变换，这个参数值是最小线长度；
- 对于多尺度霍夫变换，这个参数值是srn；
可选参数2：代表第二个可选独立参数：
- 对于经典霍夫变换，这个参数是没用的（0）；
- 对于概率霍夫变换，这个代表同一条直线上线段之间的最大间距，如果小于这个最大间距，两条线将被视为同一条直线；
- 对于多尺度霍夫变换，这个参数值是stn；

总之，面向直线检测，本函数适用于标准和标准多尺度霍夫变换算法。

案例分析

我们跑一个实例，比如下面这张田字格的图片，我们试图把田字格的行列直线全部提取出来，原图如下图所示：

在这里插入图片描述

写一个简单的霍夫变换直线检测程序，代码如下图所示：


img = cv2.imread('squares.jpg')
l0 = img.shape
print('l0:', l0[0])
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,200,apertureSize = 3)
lines = cv2.HoughLines(edges,1,np.pi/180,300)
print('lines', lines[0], type(lines), lines.shape)
for line in lines:
    for rho,theta in line:
        a = np.cos(theta)
        b = np.sin(theta)
        x0 = a*rho
        y0 = b*rho
        x1 = int(x0 + 1000*(-b))
        y1 = int(y0 + 1000*(a))
        x2 = int(x0 - 1000*(-b))
        y2 = int(y0 - 1000*(a))
        cv2.line(img,(x1,y1),(x2,y2),(0,0,255),3)
self.show_img(edges, 'canny')
self.show_img(img,'results')