[人工智能]7.opencv——边缘检测（ 拉普拉斯(Laplacian)，Sobel，Canny边缘检测）

边缘检测

\qquad 各类图像中,由于不同物体对电磁波的反射特性不同,在物体与背景、不同物体的交接处,图像的灰度将发生明显的变化,在图像中产生了边缘。边缘检测技术利用灰度的变化信息检测物体边缘,得到物体的轮廓,实现图像分割。边缘检测是所有基于边界的分割方法的第一步。
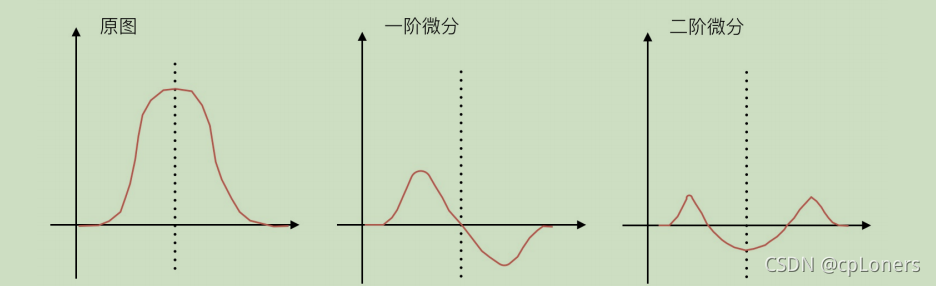
\qquad 如下图所示,沿着剖面线从左到右经过时,在进入和离开斜面的变化点,一阶导数为正。在灰度级不变的区域,一阶导数为 0；在边缘与黑色一边相关的跃变点二阶导数为正数,在与亮色一边相关的跃变点二阶导数为负数,沿着斜坡和灰度为常数的区域为 0。
\qquad 一阶导数可以用于检测图像中的一个点是否是边缘点（数字图像中一阶导数用梯度计算)；二阶导数可以用于判断一个边缘像素是在边缘亮的一边还是暗的一边（数字图像中二阶导数用拉普拉斯算子计算)。为在噪声的影响下准确得到物体的边缘信息,需要先去噪,然后提取物体边缘。一般使用平滑模板或中值滤波等平滑滤波方法消除噪声；使用拉普拉斯、Sobel等边缘提取模板突出物体的边缘,然后进行二值化处理,得到物体的边缘信息。

拉普拉斯(Laplacian)边缘检测

\qquad 拉普拉斯边缘检测的性能虽然不错,但是要进行二阶微分的运算,会把图像中的噪声扩大。在实际应用中,通常都是先用高斯函数将图像进行预先平滑,然后用拉普拉斯边缘检测找出图像中的陡峭边缘。
拉普拉斯是用二阶差分计算边缘的，连续函数的情况下1. 在一阶微分图中极大值或极小值处，认为是边缘。2.在二阶微分图中极大值和极小值之间的过 0 点，被认为是边缘。

拉普拉斯算子推导：
一阶差分：f '(x) = f(x) - f(x - 1)
二阶差分：f '(x) = (f(x + 1) - f(x)) - (f(x) - f(x - 1))
化简后：f '(x) = f(x - 1) - 2 f(x)) + f(x + 1)
提取前面的系数：[1, -2, 1]
二维的情况下，同理可得
f '(x, y) = -4 f(x, y) + f(x-1, y) + f(x+1, y) + f(x, y-1) + f(x, y+1)
提取各个系数，写成模板的形式:
$$?\begin{array}{ccc}0& 1& 0\\ 1& ?4& 1\\ 0& 1& 0\end{array}?$$
\qquad Laplacian（拉普拉斯）边缘检测使用图像矩阵与拉普拉斯核进行卷积运算，其本质是计算图像中任意一点与其在水平方向和垂直方向上4个相邻点平均值的差值。常用的拉普拉斯核如下：
$$?\begin{array}{ccc}0& 1& 0\\ 1& ?4& 1\\ 0& 1& 0\end{array}?$$
$$?\begin{array}{ccc}0& ?1& 0\\ ?1& 4& ?1\\ 0& ?1& 0\end{array}?$$
$$?\begin{array}{ccc}0& 2& 0\\ 2& ?8& 2\\ 0& 2& 0\end{array}?$$
$$?\begin{array}{ccc}0& ?2& 0\\ ?2& 8& ?2\\ 0& ?2& 0\end{array}?$$

cv2.Laplacian()函数用于实现Laplacian边缘检测，其基本格式如下：

dst=cv2.Laplacian(src,depth,ksize,scale,delta,borderType) 

其参数说明如下：

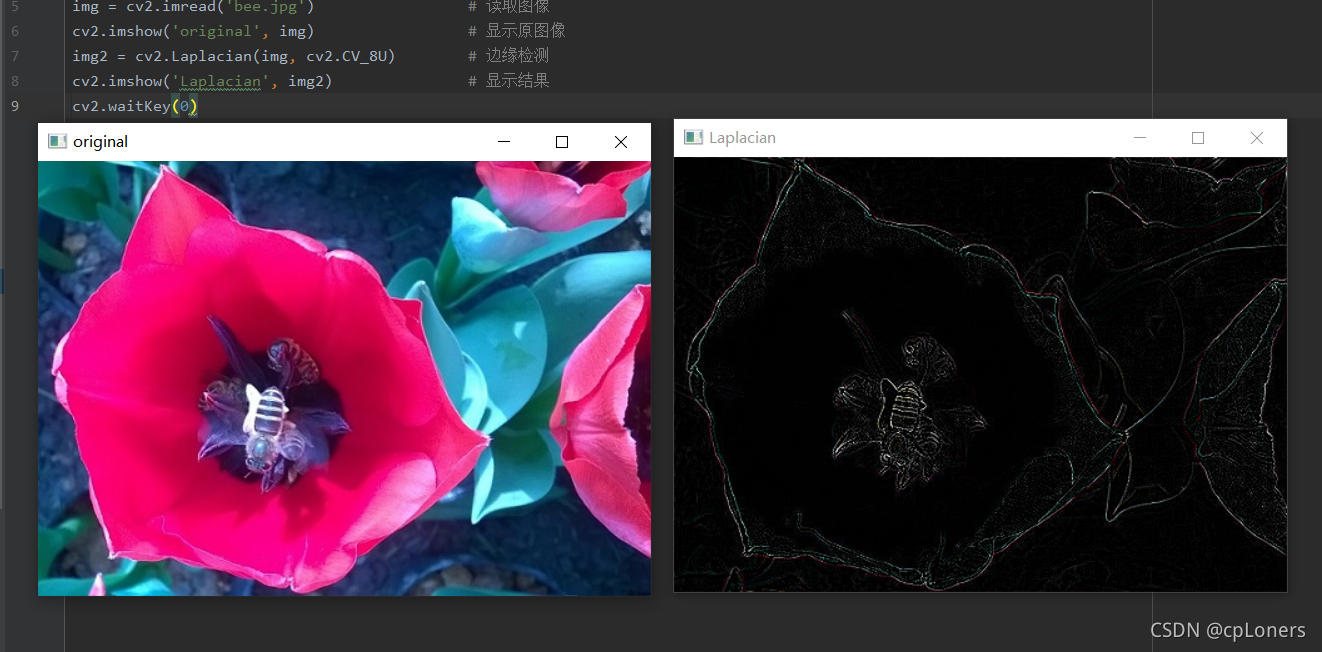
import cv2


img = cv2.imread('bee.jpg')  		        # 读取图像
cv2.imshow('original', img)  	            # 显示原图像
img2 = cv2.Laplacian(img, cv2.CV_8U) 	    # 边缘检测
cv2.imshow('Laplacian', img2)  	            # 显示结果
cv2.waitKey(0)

Sobel边缘检测

Sobel算子对图像中的每个像素,考察上、下,左、右邻点灰度的加权差,与之接近的邻点的权值较大。据此,定义 Sobel 算子如下：
$$\begin{gathered} S(i,j)=|(f(i?1,j?1)?2f(i?1,j)+f(i?1,i+1))?(f(i+1,j?1) \\ ?2f(i+1,j)+f(i+l,ji+1))|+|(f(i?1,j—1)?2f(i,j—1) \\ +f(i+1,j?1))?(f(i+1,j+1)?2f(i,j+1)+f(i+1,j+1))| \end{gathered}$$
适当取门限 TH。作如下判断:若 S(i,j)>TH,则(i,j)为阶跃状边缘点,而(S(i,j))则是边缘图像。Sobel算子具有一定的噪声抑制能力,检测效果较为理想,但所得边缘较粗,至少为两像素。
Sobel边缘检测将高斯滤波和微分结合起来执行图像卷积运算，其结果具有一定的抗噪性。
cv2.Sobel()函数用于实现Sobel边缘检测，其基本格式如下：

dst=cv2.Sobel(src,depth,dx,dy,ksize,scale,delta,borderType) 

其参数说明如下：

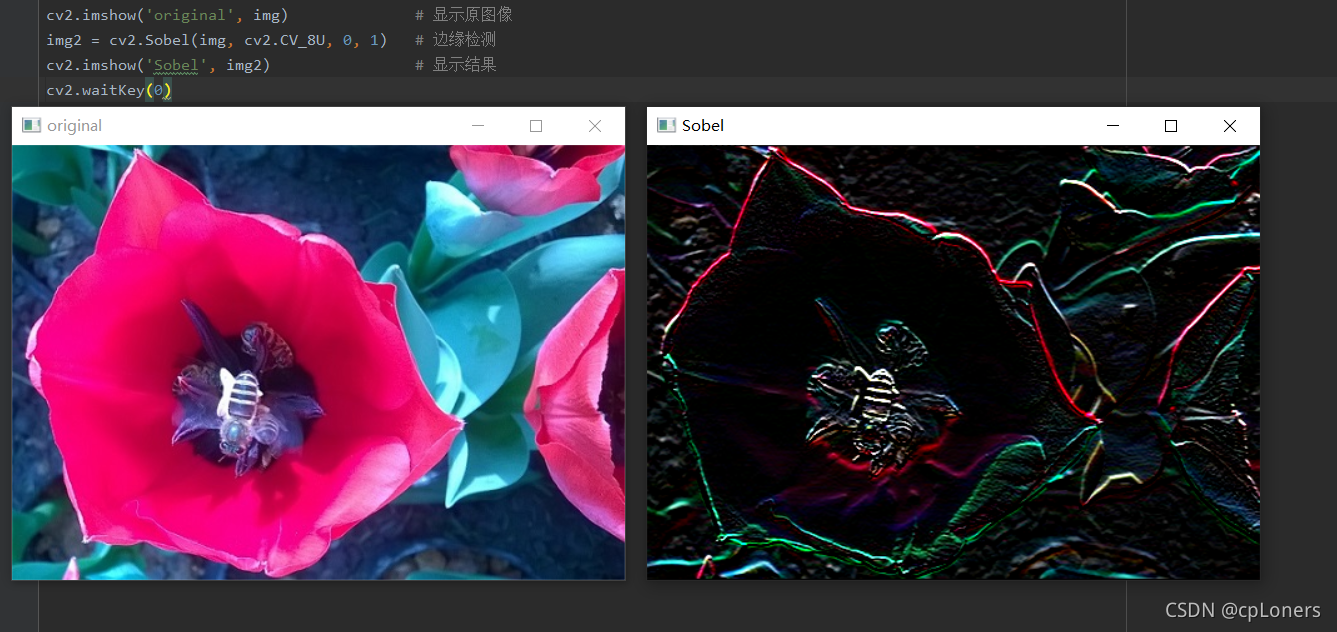
import cv2


img = cv2.imread('bee.jpg')  	         # 读取图像
cv2.imshow('original', img)  	         # 显示原图像
img2 = cv2.Sobel(img, cv2.CV_8U, 0, 1)   # 边缘检测
cv2.imshow('Sobel', img2)  	             # 显示结果
cv2.waitKey(0)

Canny边缘检测

Laplacian边缘检测和Sobel边缘检测都是通过卷积运算来计算边缘，它们的算法比较简单，因此结果可能会损失过多的边缘信息或有很多的噪声。 而Canny边缘检测的算法更复杂，它包含下列5个步骤：
（1）使用高斯滤波去除图像噪声。
（2）使用Sobel核进行滤波，计算梯度。
（3）在边缘使用非最大值抑制。
（4）对检测出的边缘使用双阈值以去除假阳性。
（5）分析边缘之间的连接性，保留真正的边缘，消除不明显的边缘。
cv2.Canny()函数用于实现Canny边缘检测，其基本格式如下:

dst=cv2.Canny(src,threshold1,threshold2,apertureSize,L2gradient) 

其参数说明如下：

import cv2


img = cv2.imread('bee.jpg')  	            # 读取图像
cv2.imshow('original', img)  	            # 显示原图像
img2 = cv2.Canny(img, 200, 300)             # 边缘检测
cv2.imshow('Canny', img2)  	                # 显示结果
cv2.waitKey(0)

拉普拉斯(Laplacian)，Sobel，Canny对比