function plotData(X, y)

figure; hold on;

pos=find(y==1);                       % y=1时的位置
neg=find(y==0);                       % y=0时的位置

plot(X(pos,1),X(pos,2),'k+','lineWidth',2,'MarkerSize',7);
plot(X(neg,1),X(neg,2),'ko','MarkerFaceColor','y','MarkerSize',7);

hold off;

end

数据分布如下图所示：

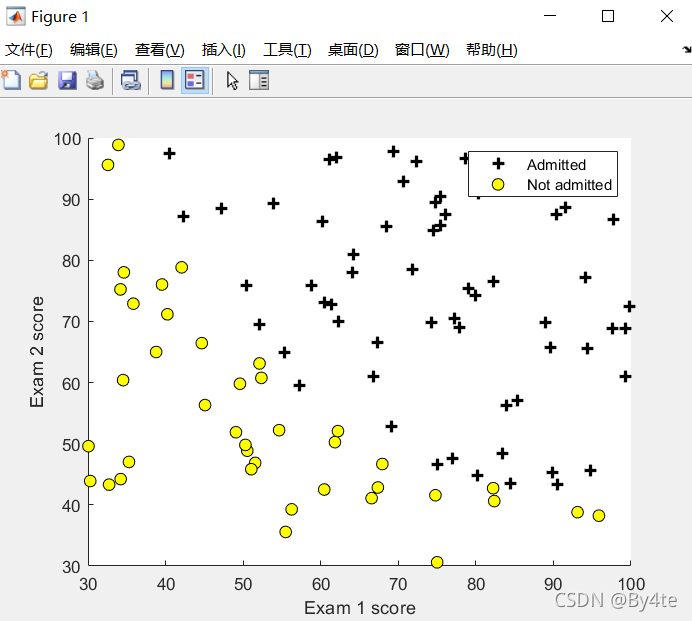
1.2 执行

1.2.1 sigmoid函数

逻辑回归假设函数为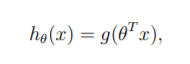

其中sigmoid函数为?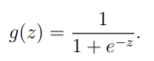

function g = sigmoid(z)

g = zeros(size(z));

g=1./(1+exp(-z));

end

1.2.2 代价函数和梯度下降

function [J, grad] = costFunction(theta, X, y)

m = length(y); % number of training examples

J = 0;
grad = zeros(size(theta));

part1 = -1 * y' * log(sigmoid(X * theta));
part2 = (1 - y)' * log(1 - sigmoid(X * theta));
J = 1 / m * (part1 - part2); 
grad = 1 / m * X' *((sigmoid(X * theta) - y));

end

1.2.3 使用高级优化算法

以下代码提供决策边界

function plotDecisionBoundary(theta, X, y)

plotData(X(:,2:3), y);
hold on

if size(X, 2) <= 3
    
    plot_x = [min(X(:,2))-2,  max(X(:,2))+2];

    plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));

    plot(plot_x, plot_y)
   
    legend('Admitted', 'Not admitted', 'Decision Boundary')
    axis([30, 100, 30, 100])
else
    
    u = linspace(-1, 1.5, 50);
    v = linspace(-1, 1.5, 50);

    z = zeros(length(u), length(v));
   
    for i = 1:length(u)
        for j = 1:length(v)
            z(i,j) = mapFeature(u(i), v(j))*theta;
        end
    end
    z = z'; 

    contour(u, v, z, [0, 0], 'LineWidth', 2)
end
hold off

end

1.2.4 评估Logistic回归

function p = predict(theta, X)

m = size(X, 1); % Number of training examples

p = zeros(m, 1);

p=round(sigmoid(X*theta));   %round取整。大于0.5为1，小于0.5为0

end

2.正则logistic回归

对微芯片质量进行检测

2.1 数据可视化

通过数据可视化，显示数据集中的所有数据。

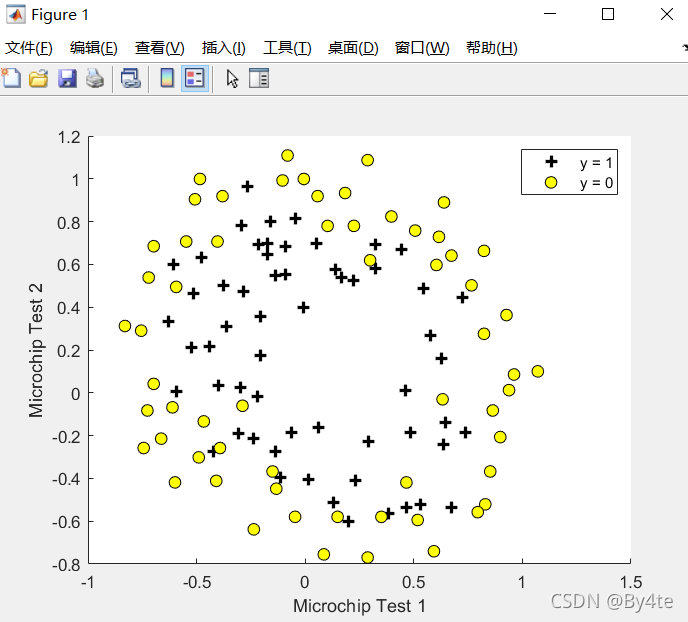
?通过观察数据图像可知，这两类数据不能通过一条直线加以区分，因此对于logistic回归，需要找到其决策边界。

2.2 特征映射

更好地拟合数据的一种方法是从每个数据创建更多特征指向。

function out = mapFeature(X1, X2)
%   MAPFEATURE(X1, X2) maps the two input features
%   to quadratic features used in the regularization exercise.
%   Returns a new feature array with more features, comprising of 
%   X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc..
%   Inputs X1, X2 must be the same size

degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end

end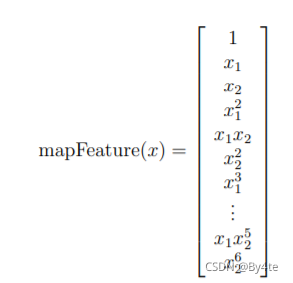

过拟合问题可使用正则化解决

2.3 代价函数和梯度? ? ? ???

function [J, grad] = costFunctionReg(theta, X, y, lambda)

m = length(y); % number of training examples

J = 0;
grad = zeros(size(theta));

part1=-1*y'*log(sigmoid(X*theta));
part2=(1-y')*log(1-sigmoid(X*theta));
part3=lambda*theta'*theta/2*m;

J=1/m*(part1-part2)+part3;

grad=1/m*(sigmoid(X*theta)-y)*X'+lambda*theta/m;

end